
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегралы в правых частях формул (29.5) и (29.6) называютсяСодержание книги
Поиск на нашем сайте
D b повторными (или двукратными), а интегралы и,y)dy и j/(x, у) dx Называются внутренними.
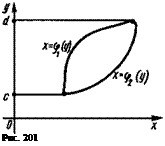
ле (29.5) подразумевается дважды произведенное интегрирование. Первое интегрирование (внутреннее) по переменной у совершается в пределах от с до d в предположении, что я: остается постоянным; результат интегрируется по переменной х в пределах от а до Ь. Если вычисление двойного интеграла выполняется по формуле (29.6), то порядок интегрирования меняется; внутренний интеграл вычисляется по переменной х, причем у сохраняет постоянное значение, а внешнее (повторное) интегрирование производится по переменной у. 2) Если область D такова, что любая прямая, проходящая внутри этой области и параллельная оси Оу, пересекает ее границу в двух точках (рис. 199 и 200), то эта область называется простой относительно оси Ох и определяется системой неравенств вида а^х^Ь, ф!(х)<^<ф2(х). В этом случае двойной интеграл выражается через повторный интеграл по формуле ъ ф2 <*) jj/(x, y)dxdy=jdx j” f(x, y)dy. (29.7) D a *1 <*> 3) Если граница области D пересекается в двух точках всякой прямой, проходящей внутри этой области и параллельной оси Ох (рис. 201), то эта область называется простой относительно оси Оу и определяется системой неравенств вида c^y^d, ФхО'Цх^ФгМ- В этом случае двойной интеграл выражается формулой d 92 (у) JJ f{x,y)dxdy=^dy J /(х, у) dx, (29.8) D с *, о>>
4) В случае, изображенном на рис. 202, область Dl определяется системой неравенств а^х^с, cpi(x)<j><cp2(х), а область Z>2—системой неравенств с^х^Ь, q>i{x)^y^q>3(x), и, значит, С Ч>2 (*) ь Ч»з (X) \^fdxdy=Qfdxdy+ \^fdxdy = ^dx J fdy+\^dx J fdy. (29.9) D Dl D2 а Ф1 (x) с (x) 3 12 12 Вычислим сначала внутренний интеграл по переменной у, считая х постоянным: х 2 + 4 х 2 + 4 | = | ^ = ^№2+4 = ^(*2 + 4-2Н+2*'2- 2 2 Теперь вычислим внешний интеграл по переменной х, подставив в него полученное выражение:
з _ _
17. Вычислить двойной интеграл ограниченной прямыми х=2, х = 6, у— 1 и у = 4. 442 О Область D является простой относительно осей Ох и Оу (рис. 203), поэтому у =4 для вычисления интеграла можно использовать любую из формул (29.5) или (29.6). Сначала вычислим двойной интеграл по формуле (29.5): 6 4
D 2 1 Вычислив внутренний интеграл по переменной у при постоянном х, находим |(jc+y)<fy=^+^-J =(4х+8)-^хН^ = Зх+у.
|
||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.117 (0.009 с.) |



 ь d
ь d J*<£xjV(x, y)dy
J*<£xjV(x, y)dy где интегрирование сначала выполняется по переменной х, а затем по переменной у.
где интегрирование сначала выполняется по переменной х, а затем по переменной у.
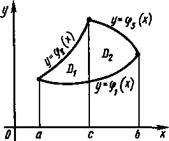 Рис. 202
Рис. 202
 Если нижняя или верхняя линии границы состоят из нескольких участков, имеющих различные уравнения, то область D необходимо разбить прямыми, параллельными оси Оу, на такие части, чтобы каждый из участков выражался одним уравнением. В этом случае вычисление двойного интеграла сводится к вычислению двух (и более) повторных интегралов.
Если нижняя или верхняя линии границы состоят из нескольких участков, имеющих различные уравнения, то область D необходимо разбить прямыми, параллельными оси Оу, на такие части, чтобы каждый из участков выражался одним уравнением. В этом случае вычисление двойного интеграла сводится к вычислению двух (и более) повторных интегралов. x 2 + 4 j* j >•
x 2 + 4 j* j >• |(1+2лГ^=[*-^Дз-?)-(1-2)=3;
|(1+2лГ^=[*-^Дз-?)-(1-2)=3; ^(x+y)dxdy =^dx j*( x+y)dy .
^(x+y)dxdy =^dx j*( x+y)dy .


