
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия над комплексными числами, заданными в тригонометрической формеСодержание книги
Поиск на нашем сайте 1. Тригонометрическая форма комплексного числа. Пусть r=\a+bi\ = = у/а2 + Ь2 — модуль, а ф—одно из значений аргумента комплексного числа a+ bi. Так как из соотношений (14.3) вытекает, что а=г совф, b=г sin ф, то а-|- bi=г (cos ф + / sin ф). (14.5) Таким образом, любое комплексное число а+Ыф 0 можно записать по формуле (14.5), где г—модуль, а ф — одно из значений аргумента этого числа. Верно и обратное утверждение: если комплексное число a+bi представлено в виде (14.5), где г>0, то r=\a+bi\, ф = а^(а+6/). Представление комплексного числа в виде z = г (cos ф Н- / sin ф), где г> 0, называется тригонометрической формой записи комплексного числа. Для представления комплексного числа z = a+bi в тригонометрической форме необходимо найти: 1) модуль этого числа; 2) одно из значений аргумента этого числа. В силу многозначности argz тригонометрическая форма комплексного числа также неоднозначна. 2. Действия над комплексными числами, заданными в тригонометрической форме. Произведение комплексных чисел z1=r1(cos91 + /sin91) и z2 = r2 (cos ф2 + / sin ф2) находится по формуле v! (cos фх + /sin ф!) • г2 (cos ф2 + isin ф2) = гxr2 [cos (Ф1 + ф2) +1 sin (Ф1 + ф2) ], (14.6) т. е. ki z21 = гi ■ г2 = |z, I • |z21, arg (ziz2)=<p j+<p2. Таким образом, при умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются. Частное комплексных чисел = (со8ф! +/sin91) и z2 = r2(со8ф2 + + /sтф2) находится по формуле ^(совф^/втф!) г1г.. — г= [cos (ф! ф2)“Ь f sin (фг ф2)], (14.7) Г2 (cos ф2 +1 Sin ф2) Г2 т. е. ri I Zj| Zi =-=Г1’ аг§-=ф1-ф2. г2 |z2| z2 Таким образом, при делении комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются. Для возведения комплексного числа г(со8ф + /8Шф) в п-ю степень используется формула [г(с08ф + ШПф)]" = г"(с08Иф + ШПЖр), Л?= Z, (14.8) которая называется формулой Муавра. Для извлечения корня п-й степени из комплексного числа г (cos ф 4-г sin ф) используется формула ------ 7 г(Ф + 271А:.. ф + 2лА:\ z^ = y (cos ф + f sin ф)=т I cos--------- Ь i sin------- 1, (14.9) где \fr—арифметический корень, k = 0, 1, 2,1. 29. Представить в тригонометрической форме следующие числа: 2; 2)6i; 3) -2 + 2^3/; 4) 2—2*; 5) -у/3-i. О 1) Здесь а = 2, Ь=О, г=2. Так как вектор, изображающий число 2, лежит на положительной полуоси Ох, то главное значение аргумента ф = 0; следовательно, 2 = 2 (cos 0 + / sin 0) или 1 = 2 (cos 2кк+/ sin Ink), k^Z. 1) Здесь a = 0, b = 6, r=6. Поскольку вектор, изображающий число 6/, лежит на положительной полуоси Оу, главное значение аргумента ф = я/2; поэтому 6/=6 [cos (я/2) + / sin (7i/2) ] или 6/=6 [cos (n/2+2пк) + / sin (n/2+2я£) ], к е Z. 2) Здесь а =—2, Ь = 2у/3, г=4. Точка, изображающая число z, лежит во II четверти; tg ф = 2^/3/(— 2)= — >/3, ф = 2я/3. Значит, —2+2ч/3/=4 [cos (2я/3) + / sin (2я/3) ] или — 2 + 2^/3/=4 [cos(2я/3+2я£) + /sin(2я/3 + 2пк)], fceZ. 3) Здесь а = 2, Ь= —2, г=2^/2. Точка, изображающая число z, лежит в IV четверти; tg ср = — 1, ф = — я/4. Поэтому 2—2i=2^/2 [cos (—я/4) + / sin (—я/4) ] или 2— 2i=2y/2 [cos(— K/4+2nk) + ism(—n/4+2nk)], bZ. 4) Здесь а=—у/3, b= — 1, г=2. Точка изображающая число z, лежит в III четверти; tgф = l/^/з, ф=—5я/6, тогда — у/b — /=2 [cos (—5я/6) +1 sin (—5я/6) ] или — у/b — i=2 [cos(—5rc/6+2rc£) + /sin(— 5п/6+2пк)], k<=Z. ф 30. Представить в алгебраической форме числа: 1) z = 2 (cos 2и + / sin 2тс); 2) z = ^/2 [cos (Зтс/4)+/ sin (Зтс/4) ]. О 1) Подставив значения соз2я=1, 8т2я = 0 в данное равенство, получим z = 2 (1Ч- / * 0) = 2. 2) Имеем z=v/2 [cos(Зя/4) + isin(Зя/4)] = Jl [-v/2/2+i(v/2/2)]= -1 +». • 31. Найти произведение 2 [cos (тс/6) + / sin (тс/6) ]• 3 [cos (тс/12) +/sin (тс/12)]. О По формуле (14.6) получим 2 [cos (71/6) + / sin (тс/6) ] • 3 [cos (я/12) + / sin (те/12) ] = 2 * 3 [cos (я/6+я/12) + + / sin (я/6 + я/12)] = 6 [cos (я/4) + / sin (я/4) ] = 6 [(>/2/2) + / (^2/2) ] = = 3n/2+3i7'2. • 32. Выполнить деление: 10 [cos (Зя/4) +/sin (3/я/4)]:2 [cos (я/4) + /sin (я/4)]. О По формуле (14.7) находим 10 [cos (Зя/4) + / sin (Зя/4) ]: 2 [cos (я/4) + / sin (я/4) ] = = (10/2) [cos (Зя/4—я/4) + / sin (Зя/4—я/4) ] = 5 [cos (я/2) + / sin (я/2) ] = = 5(0 + /) = 5/. • 33. Возвести в степень: 1) [cos (я/6)+ /sin (я/6) ]6; 2) [3/2 — -(УЗ/2)/]10. О 1) По формуле Муавра получим [cos (я/6) + / sin (я/6) ]6 = cos [6 • (я/6) ] + / sin [6 • (я/6) ]=cos я + / sin я = = -1+/0=-1. 2) Представим данное число в тригонометрической форме. Здесь я = 3/2, Ь=— -Уз/2, т. е. г=^/(3/2)2 + (—>/з/2)2 = >/з. Точка, изображающая данное число, лежит в IV четверти, поэтому tgcp = (—N/3/2):(3/2) = — >/3/3, т. е. ср = — я/6. Итак, 3/2—(д/3/2) /=>/3 [cos (- я/6)+/ sin (—я/6)]. Следовательно, {>/3 [cos (—я/6)+/ sin (—я/6)] }10 = 35 [cos (— 10 • я/6)+/ sin (— 10 • я/6)] = = 35 [cos (5я/3)—/ sin (5я/3)] = 35 [cos (5я/3 — 2я)—/ sin (5я/3—2я)] = = 243 [cos(я/3)+ /sin (я/3)] = 243 [1/2+/(^/3/2)]= 121,5(1 +/,/3). # 34. Применяя формулу Муавра, доказать справедливость следующих тождеств: cos 2ф = cos2 ф — sin2 ф; sin 2ф = 2 sin ф cos ф; cos Зф = 4 соз3ф — 3 cos ф; sin Зф = 3 sin ф — 4 зт3ф. О Полагая в соотношении (14.8) г— 1 и п — 2, получим (cos ф + / sin ф)2 = cos 2ф + / sin 2ф, или cos2 ф + 2/ cos ф sin ф — sin2 ф=cos 2ф + / sin 2ф. Из условия равенства двух комплексных чисел следует, что cos 2ф = cos2 ф — sin2 ф; sin 2ф = 2 sin ф cos ф. Аналогично, полагая в соотношении (14.8) r= 1 и п = 3, имеем (cos ф + / sin ф)3=cos Зф + / sin Зф, т. е. cos3 ф + 3/ со82ф sin ф — 3 вт2ф cos ф — / sin3 ф=cos Зф+/ sin Зф. Из условия равенства двух комплексных чисел следует: cos Зф = cos3ф — 3 sin2ф cos ф = cos3 ф — 3(1 — cos2ф) cos ф = 4 cos3 ф — 3 cos ф; sin Зф = 3 cos2 ф sin ф — sin3ф = 3 (1 — 8Ш2ф) sin ф—sin3ф = 3 8Шф—4 sin3ф. # 35. Извлечь корни из комплексных чисел 1) y/i; 2) О 1) Представим число / в тригонометрической форме: /=0+1*1 = =cos (л/2) + / sin (я/2). По формуле (14.9) получим г. /- 7“^—.. / п/2 + 2кк.. к/2 + 2кк zk = y/l = у/ cos (я/2) +1 sin (я/2)=cos-- h i sin = =С08(я/4+я/:) + /8т(я/4+я/:), k=0, 1; если k = 0, to z0=cos (я/4) +/sin (я/4) = у/2/2+ (^/2/2)/; если k= 1, to z! = cos (я/4+я)+/ sin (я/4+я) = — cos (я/4)—/ sin (я/4) = — у/2/2 — -(n/2/2)*. 2) Представим число 1 в тригонометрической форме: 1 =cos0+/sin0. По формуле (14.9) находим г!---------------- г— 0+2я£ 0+2я/г zk = y\ = ycos0+/sin0=cos— h/sin—-—= =С08(2яА:/3) + /8т(2яА:/3), к=0, 1, 2; если к = 0, то zo=cos0+/sin0= 1; если к = 1, то z j = cos (2я/3) + / sin (2я/3) = — 1 /2+(>/3/2) /; если к = 2, то z2=cos (4я/3) + / sin (4я/3) = — 1 /2—(>/3/2) /. 36. Представьте в тригонометрической форме комплексные чис- ла: 1) Зг; 2) -1 + г; 3) 1-/^3; 4)^3-/; 5) ^/3/2—(1/2)г; 6) -3+4/. 37. Представьте в алгебраической форме числа: 1) 5 [cos (я/2) + + / sin (я/2) ]; 2) 4 [cos (—я/3) + / sin (—я/3) ]; 3) cos я + / sin я; 2 [cos (я/4) + / sin (я/4) ]; 5) 3 (cos 0 + / sin 0). 38. Найдите произведения: 1) 3 [cos (я/8) + / sin (я/8) ] • [cos (5я/24) + / sin (5я/24) ]; 2) 2 [cos (я/3) + / sin (я/3) ] • 5 [cos (— я/4) + / sin (- я/4) ]; 3) (cos5 + /sin5) (cos2 + /sin2); 4) [cos (2я/3) + / sin (2я/3) ] • [cos (—я/2) + / sin (—я/2) ]; 5) 4 (cos 10° + / sin 10°) • 2 (cos 35° + / sin 35°); 6) [cos (5я/6) + / sin (5я/6) ] • [cos (2я/3) + / sin (2я/3) ]. 39. Выполните умножение, используя тригонометрическую форму комплексного числа: 0+5')(-^+^) 2)<l+.V3)(-2-21V3); 3) (1+0(3 + 3/^3); 4) (6 + 2г\/3)(—3 —Зг); 2) (5 + 5/)(cos 15° + / sin 15°); 3) 3 [cos (—я/8)+г sin (—я/8) ] • (3+>/Зг)- 40. Выполните деление в тригонометрической форме: 1) 3 [cos (Зя/4) + i sin (Зя/4) ]: [cos (я/2) + i sin (я/2) ]; 2) (cos210° +/sin210°):(cos 150° + /sin 150°); 3) [cos(— я/3) + шп(—я/3)]: [cos(— n/6) + ism(— я/6)]; 4) (cos 150° + i sin 150°): [cos (-120°) + i sin (-120°) ]. 41. Возведите в степень:
42. Вычислите: 1) (1 -012+0 + 012; 2) -)8 ■ 43. Извлеките корни: 1) \J— 1; 2) 3) \fi;4) i/4; V-2+2/УЗ; 6) %Д. § 4. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ С КОМПЛЕКСНЫМ ПОКАЗАТЕЛЕМ. ФОРМУЛЫ ЭЙЛЕРА
(14.10) (14.11) которое называется формулой Эйлера. Для комплексных показателей остаются в силе основные правила действий с показателями; например, при умножении чисел показатели складываются, при делении — вычитаются, при возведении в степень—перемножаются. Показательная функция имеет период, равный 2я/, т. е. ez+2ni = ez. В частности, при z=0 получается соотношение e2ni = l. Тригонометрическую форму комплексного числа z=r (cos ср 4- / sin ср) можно заменить показательной формой: (14.12)
(14.13) (14.14) (14.15) __ _ ф + 2яЛ. "Jre*=iJr-e " ' (к=0, 1, 2,..., л-1). (14.16) Формула Эйлера (14.11) устанавливает связь между тригонометрическими функциями и показательной функцией. Заменив в ней у на ф и на — ср, получим еф1=cos ф + i sin ф, е ~ф1=cos ф — i sin ф. Складывая и вычитая эти равенства, получим cos ф=(еф1 + е-ф1)/2, (14.17) sin ф = (е* -)/(2/). (14.18) Эти две простые формулы, также называемые формулами Эйлера и выражающие тригонометрические функции через показательные, позволяют алгебраическим путем получить основные формулы тригонометрии. 44. Найти: 1) е'*/4; 2) е*е~"'2; 3) е2+ы. О По формуле (14.11) получим: 1) еЫ1* - cos (те/4) + i sin (тг/4)=^2/2+ЦуД/2); 2) ет “ =e"[cos(-«/2)+iSm(^n/2))=e-,i=c0s(-re) +,-sin(-Jt)= - 1; 3) по формуле (14.10) получим e2+I7t=e2(cosrc + /sin7i)= — е2. ф 45. Найти: l)cos/; 2)cos(l— i). О По формуле (14.17) получим: . е1 +е-*2 е~1+е е2 + \ ,) с,,--------------------------------- cos(l —1)= = =-[e(cos 1 +/sin 1)+ + e-1 (cos(— l)H-/sin(— l)]=i[ecos 1 +e/sin 1 +e_1cos 1 — e2 +1 e2 — 1 —e_1/sin l]=-[(e+e_1)cos 1 +i(e—e~l)sin l]=—-—cos 1 +/ —— sin 1. ф 46. Показать, что для комплексного переменного z справедливы формулы: 1) sin2z+cos2z = 1; 2) sin 2z = 2 sin z cos z; 3) cos 2z = = cos2z—sin2z. О 1) Возведя обе части равенств (14.17) и (14.18) в квадрат и затем почленно складывая их, получим , (ezi + e~zi)2 (ezi-e-zi)2 e2zi+ 2+e~2zi-e2zi+ 2-e~2zi cos z+sin z=-------- —-—h-------- =------------------------------------------- =1. —4 4 2) Перемножив левые и правые части равенств (14.17) и (14.18), получим ezi+e~zi ezi—e~zi e2zi-e~2zi 2sinzcosz=2----------- •----------- =------------- =sin2z. 1 21 2 i 3) Возведя обе части равенств (14.17) и (14.18) в квадрат и почленно их вычитая, получим 2 . 2 (ezi+e~zi)2 lezi-e-zi)2 cosz—sin2z=------- —------------ —= 4 -4 e2zi + 2+e~2zi + e2zi—2 + e~2zi e2zi+e~2zi =------------------------------------- =------------- =cos2z. 4 2 47. Представить в показательной форме числа: l)z=2i; 2) z— — 1 + i. О 1) Здесь я =О, 6=2, г=2, ф = те/2. По формуле (14.12) получим z=2einl2. Здесь а= — 1, b= 1, r= 2, tgф = — 1, ф = Зя/4. По формуле (14.12) имеем z= s/2e3nil4‘. ф 48. Представив числа z1 = l-\-iи z2 = \ — iyjbв показательной форме, вычислить: 1) zxz2; 2) zi/z2; 3) zf; 4) ^/z^. О Для числа z1 = lH-i имеем: а= 1, 6=1, г= 2, ф = я/4, т. е. Zj = = *j2eim. Для числа z2 = l — />/3 имеем: д= 1, 6= —>/3, г=2, ф= — тг/З, т. е. z2 = 2е-1я/3. 1) По формуле (14.13) находим ZjZ2= у/2е1п14' •2е_,я/3 = 2л/2е“1я/12. 2) По формуле (14.14) получим 21 _\/2е Я/ m/4-(-fa/3)_V^ 7яЁ/12 z2 2е-£я'3 2 2 3) По формуле (14.15) имеем zf=(Л/2е1я/4)6 = 8е13я/2. 4) По формуле (14.16) находим Zfc= 4/^=уу2<>/4= 8/2e(n/4+lnk)il4, к=О, 1, 2, 3; если fc=0, то z0= */2еы/16; если fc=l, то z1== 8/2е(я/4+2я)1/4= феш,16\ если fc=2, то z2= в/2е(я/4+4я){/4= 0.ellai/16= */2e~15ni/16; если fc=3, то z3=*/2einl*+6*yil*= *fie25*i/16= 0.е~™116. ф 49. Найдите: 1) е1; 2) е*я; 3) e1 + i; 4) е*я/2; 5) е*я/3; 6) е4+3‘; 7) е2"‘; 8) е3|“2. 50. Найдите: 1) sin/; 2) cos(l+/); 3) sin (1 — /). 51. Покажите, что для комплексного переменного z справедливы равенства: cos(—z) = cosz; sin(—z)= — sinz; .. -. „ • • о 1—cos2z о l+cos2z sin3z=3sinz —4sinJz; sin^z=----; cos^z=. 2 2 52. Представьте в показательной форме числа: 1) 1; 2) у/3 + i; 2) 3 + 1^3; 4) -72+1^6. 53. Представив числа zt = у/з + i и z2 = y/l+iy/2 в показательной форме, вычислите: 1) ztz2; 2) zjz^, 3) z\\ 4) 5) f[z2. §5. СМЕШАННЫЕ ЗАДАЧИ 54. Выполните умножение: 1) (ау/Ь+Ыу/а)(—ау/Ь—Ыу/а); 2) (у/ф-iy/b/a)-(y/b/a+i у/а/Ь). 55. Разложите на множители: 1) 4. x:2+25; 2) а2+ 12;3) х/5+9; у/2+у/з. С* ГУ cz 1 \ 9т2 + 4п2 х+\ а + Ь 56. Сократите дроби: 1) —-------- ——; 2) ———; 3) Ът 2 in y/x+i y/a+iy/b 57. Выполните деление: 1) + 2) ni\f™ y/b + iy/2 Пу/m+miy/n 58. Найдите модуль и аргумент комплексного числа j-. 59. Проверьте равенство >/^+г\А_лА+гЧ/^ = 2(т п) фп-iyfi yfa-iyfin ™+п 60. Найдите числовые значения многочленов: 1) jc15 + x14 + + 3л:12 —xi0+x7 при x = i\ 2) x3+;x:2 + x+1 при x=\+i. (4 V ([2 Л2 61. Выполните действия: 1) —-—; 2) /-—I—). \л/з + // V 2 2/ 62. Возведением в квадрат докажите справедливость формул: 1) y/a + bi+ y/a—bi= y/2(yfa2 + b2 + a)\ 2) y]a+bi— y/a—bi=iy/2(y/a2 + b2 — a). 63. Покажите, что если а = — 0,5 (1 -h / у/з), Ъ = 0,5 (— 1 + / у/з), то: 1) аъ = 1; 2) b3=1; 3) а2 = Ь; 4) 62 = а. 64. Докажите, что jc3+j3 — Зху = — 1, если х=—0,5 +1,5/ и у= —0,5 —1,5/. 65. Произведите указанные действия: 1 ~ч 1 1 1+/ 1— / !) (Гйр+(М1; } (Т+/р+(Г^р } Т^/+Т+? 66. Выполните действия в тригонометрической и показательной формах: 1) 5 [cos (я/6) — /sin (я/6)] • [cos (я/4) + /sin (я/4)]; 2) 8 [cos (я/3) + /sin (я/3)]: 4 [cos (я/12) + /sin (я/12)]. 67. Вычислите с помощью формулы Муавра: 1) [cos(я/24)+/sin(я/24)]6; 2) [cos^/10)+/sin^/10)]10. 68. Докажите, что (coscp + Zsincp)-1 =coscp — /sincp. 69. Вычислите: 1) $/i; 2) ^/l + i. 70. Решите двучленные уравнения: 1) х3—8=0; 2) 8л:3—27=0; х3+125 = 0; 4) 27х3 + 1=0; 5) х[29]+81=0; 6) х[30]-64=0. 71. Составьте квадратное уравнение с действительными коэффициентами,_корнями которого служат числа: 1) / и —/; 2) 3 + / и 3 — /; l-iy/5 и 1 + г\/5. 72. Решите биквадратное уравнение х4+х2 + 1=0, выполнив извлечение корня в тригонометрической форме. 73. Решите уравнения: 1) х6—28x427=0; 2) (2л:+3)б-9(2х+3)3+8=0. ЗАЧЕТНАЯ РАБОТА
I вариант 1) Найдите модуль и аргумент 8 + 21 числа 5 — 3/ II вариант 1) Найдите модуль и аргумент 5 + / числа 1 + 3/
2) Выполните действия: 3-4/ 2) Выполните действия: 5—4/
3) Извлеките корень ^/8. 4) Решите уравнение дс4—2л:2 + +4=0.
Глава 15 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и ее производные или дифференциалы. Символически дифференциальное уравнение записывается так: F(x, у, /)=0, F(jc, у, у")=0, F(x, у, у', у",..., /">)=0. Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного. Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение. Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество. • Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную. Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции. График частного решения дифференциального уравнения называется интегральной кривой. Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых. Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида Для решения этого уравнения нужно сначала разделить переменные: фМ а затем проинтегрировать обе части полученного равенства: x)dx. 1. Найти общее решение уравнения x(\+y2)dx=ydy. О Разделив переменные, имеем , ydy xdx=- \+у2 Интегрируем обе части полученного уравнения: у4уг, х4-Ыч-Л+'*с. 11 +у 2 2 2 Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С мы написали (1/2) In С. Потенцируя последнее равенство, получим х2 = 1п [С(\+у2)]. Это и есть общее решение данного уравнения, ф 2. Найти частное решение уравнения stgtdt + ds = 0, удовлетворяющее начальным условиям s=4 при t = n/3. О Разделив переменные, имеем ds l%tdt+ — = 0. s Проинтегрируем обе части полученного уравнения: = 1п С; —In cosf+lns=lnC, или In s=In C+In cos/, S—C cos /. Это общее решение данного уравнения. Для нахождения значения произвольной постоянной С подставим значения /=я/3 и s=4 в выражение для общего решения: 4=Ccos(ii/3), или 4=С/2, откуда С=8. Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид 5 = 8 cos/, ф Найдите общие решения уравнений: 3. 1) x2dx = 3y2dy\ 2) y/xdy = y/ydx; 3) — 3) (l+j;) </* = (*-l)<fy. 4. 1) х^Л: = (1+х2)^; 2) 2)dfy = 0. 5. 1) (x2—yx2)dy+fa2 + xy2)dx= 0; 2) x2dy—{2xy+3y)dx = $. 6. 1) (1 +j>2)</x— yfxdy = 0; 2) ^/l— x2dy—xy/\ — y2dx=0. Найдите частные решения уравнений, удовлетворяющие указанным начальным условиям: 7. 1) ydy — xdx; у = 4 при х=—2; 2)xdy=ydx; у —6 при х=2. 8. ds=(3t2—2t)dt; s=4 при t=2. ^ dy dx 9. -?=-?; ^=2 при x=0. dydx 10. =--; y — 4 при x=0. jc— 1 2 11. (1 +y)dx—(\ — x)dy\ y = 3 при x=—2. 12. — >>)л:ф> = 0; ^=1 при х=\. 13. y2dx = exdy; >>=1 при л: = 0. dx 14. —^--- =ctgjcsinydy; у = я при х = п/3. cos2 ^ cos ^ §2. ЗАДАЧИ НА СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 15. Найти закон движения тела по оси Ох, если оно начало двигаться из точки М (4; 0) со скоростью v = 2t+3t2. О При прямолинейном движении скорость есть производная от пути по _ _ dx времени. Обозначив путь через х, имеем v=—; тогда dt dx —=2t+3t2, или dx=(2t+3t2)dt. dt Проинтегрировав, получим x=t2 + t3 + C. Используя начальные условия, найдем С. Так как х=4 при /=0, то, подставив эти значения в общее решение, находим С=4. Итак, закон движения тела имеет вид х= = t2 + t3 + 4. ф 16. Составить уравнение кривой, проходящей через точку М (2; —3) и имеющей касательную с угловым коэффициентом 4jc—3. О Согласно условию, имеем —=4jc—3, или dy = (4х—3) dx. ах Проинтегрировав, получим у=2х2 — Зх+С. Используя начальные условия х=2 и у= — 3, находим С=— 5. Следовательно, искомое уравнение имеет вид у = 2х2 — Зх—5. ф 17. Вода в открытом резервуаре сначала имела температуру 70°, через 10 мин температура воды стала 65°, температура окружающей резервуар среды 15°. Определить: температуру воды в резервуаре через 30 мин от начального момента; момент времени, когда температура воды в резервуаре станет равной 20°. О Обозначим Т температуру воды в момент времени t. Скорость охлаждения воды есть скорость изменения функции, связывающей t и Т, т. е. dT производная —. dT Величина — пропорциональна разности температур воды в резервуаре и dt в окружающей его среде, т. е. к (Т—15°), где к—коэффициент пропор- dT циональности. Следовательно, —=к(Т—15°). Разделив переменные, имеем dT
\n(T-\5°)=kt+C, Т- 150=ек'+с=ек‘ес=ек,Си откуда Т=С1екг+15°. (*) Это соотношение и выражает закон охлаждения воды. Найдем величину Cj при начальных условиях Г=70° при /=0. Имеем 70=С1е*‘°+15, или 55° = ^° = ^, т. е. С1 = 550. Подставив найденное значение Сх в равенство (*), получим T=55°eht+15°. (**) Найдем величину к. По условию, Г= 65° при t =10 мин. Подставив эти значения в соотношение (**), получим 65° = 55V10+15°, или 50° = 55°е10*, или 10/11=£>1О\ Прологарифмировав последнее равенство, имеем lg 10—lg 11 = 10/rlge, откуда , 1-lgll 1-1,0414 0,0414 ‘-т4г*й1йй5--434Г--0’009532' Подставив значение к в соотношение (**), получим закон охлаждения, связывающий переменные t и Т: Т=55°е~°’009532г+ 15°. (***) Найдем температуру воды через 30 мин от начального момента. Для этого в уравнение (***) подставим значение / = 30: Г=55ое-0,009532'30+15°, или Г=55°е_0’286 + 15°. Произведем вычисления: *=55 • е -°’286, lg* = lg55 - 0,2861ge= 1,7404- 0,286 • 0,4343 = = 1,7404-0,1242= 1,6162, *=41,32*41; тогда Г=4Г + 15° = 56°. Найдем, через сколько времени температура воды в резервуаре станет равной 20°. Подставив значение Г=20° в соотношение (***), получим 20° = 55°е~°’009532* +15°, иди 5о = 55о<?"°’009532‘, откуда e-o,oo9532t=1/11^00909> ши _ од)09532* lg е=lg 0,0909 = 2,9586, т. е. 2,9586 1,041 t—---------------------------------------------- «251 мин=4 ч И мин. # 0,009532 • 0,4343 0,009532 • 0,4343 18. Вращающийся в жидкости диск замедляет свою угловую скорость за счет трения, причем сила трения пропорциональна угловой скорости. Найти: 1) скорость вращения диска в момент t=120 с, если при t=0 он вращался со скоростью 12 рад/с, а при г=10с его скорость стала 8 рад/с; 2) момент времени, когда скорость вращения диска окажется равной 1 рад/с. О Пусть со—угловая скорость вращения диска в момент времени t, d(o тогда замедление вращения диска под воздействием силы трения равно —. at d(d Согласно условию, —=/гсо, где к—коэффициент пропорциональности. dt Разделив переменные и интегрируя, получим rffi) (J frffl),г,, ^ —=kdt, —=k\dt, Inю = А*+С, ® J © J откуда (d = ekt+c = ektec9 или co=C1efct. (*) Найдем постоянную величину Сх при начальных условиях со =12 рад/с при / = 0. Подставив эти значения в равенство (*), имеем 12 = C1efe'°, т. е. 12= Cj. Таким образом, (o=\2ekt. (**) Найдем числовое значение к по следующим данным: /=10 с и со=8 рад/с. Подставим эти значения в равенство (**): 8=12е*'10, откуда е10* = 2/3, 10Л: lg е=lg 2—lg 3, Ig2-lg3_ ljg 3—lg 2_____________ 0,4771 —0,3010 lg e- 10 lg e- 10 0,4343 Подставив значение к в равенство (**), получим со= 12е~0’0405*. (***) Найдем скорость вращения диска в момент времени /=120 с. Подставим в равенство (***) значение /=120: со= 12е-0’0405’120= 12е-4,9 = 0,09 (рад/с). Определим, в какой момент времени диск будет вращаться со скоростью 1 рад/с. Подставив в соотношение (***) значение ю=1, имеем l = 12e"00405'; e-o.M05,=_L; —0,0405?lge=lg 1 —lg 12, lg 12 г=о^кг61 (c)- • 19. Найти закон движения тела по оси Оу, если оно начало двигаться из точки М(0; 6) со скоростью v = 4t—6/2. 20. Составить уравнение кривой, проходящей через точку М(2; — 1) и имеющей касательную с угловым коэффициентом к=\/(2у). 21. Составить уравнение кривой, проходящей через точку (1; 4), для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью Оу. 22. Температура воздуха равна 20°. Тело охлаждается за 40 мин от 80 до 30°. Какую температуру будет иметь тело через 30 мин после первоначального измерения? 23. Радий распадается со скоростью, пропорциональной начальному его количеству. Через сколько лет распадется половина начального его количества? Принять к=0,00044 (единица измерения времени—год). 24. Замедляющее действие трения на диск, вращающийся в жидкости, пропорционально угловой скорости. В какой момент времени скорость вращения диска окажется равной 2 рад/с, если при /=0 он вращается со скоростью 20 рад/с, а при /=8 с—со скоростью 16 рад/с? §3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА Уравнение вида —+/(*Ь+ф(*)=о, где /(х) и ф (х)—функции от х, называется линейным дифференциальным уравнением первого порядка. В частном случае /(х) и ф(х) могут быть постоянными величинами. Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки y=uz, где и и z—новые функции от х. dy 2у / v % Найти общее решение уравнения г=(*+1). dx х+1 О Это линейное уравнение: здесь f{x)=— 2/(х+1), <р(*)= — (х+1)3. Положим y=uz и продифференцируем это равенство по х: dy dz du dx dx dx dy Подставив теперь выражения для у и — в данное уравнение, получим dx dz du 2 uz. v, и —+z----------- -=(x+1), dx dx x+1 или dz (du 2u\ ,.. Так как одну из вспомогательных функций и или z можно выбрать произвольно, то в качестве и возьмем одно из частных решений уравнения du 2и - ---------- =0. Разделив в этом уравнении переменные и интегрируя, имеем dx х+1 du 2dx Cdu Г dx,.. „ч, -------- -=0, —=2 ------- 1пм=21п(х+1), w=(x+1) и x +1 J и J x +1 (произвольную постоянную С принимаем равной нулю, так как находим одно рз частных решений). Подставим теперь выражение для и в уравнение (*); тогда получим уравнение (*+1)2^=(*+1)3, или ~г—х+1- y dxK dx
(x+\)dx; zJ°y +С. Зная и и z, теперь получаем общее решение данного уравнения: ,.«.(х+,).[Ь±!)!+с].Ц!£+с(,+1)>. • 25. Найти частное решение уравнения cos xdy-\-у sin xdx — dx, если y= 1 при л: = 0. О Разделив все члены данного уравнения на cos xdx, получим уравнение dy 1 -f+y tgx= ------------, (*) dx cosx dy dz du которое является линейным. Положим y=uz; тогда —=и——\-z—. Под- dx dx dx dy, 4 ставив выражения для у и — в уравнение (*), имеем dx
du du -—bwtg*=0, т. е. —btg*d*=0, dx и откуда
cosx—=-------, или —=------- г—, т. е. z=tg*+C. dx cos* dx cos * Следовательно, общее решение данного уравнения записывается так: y = uz = cos * (tg *+С) = sin *+С cos *. Используя начальные условия у= 1, *=0, имеем 1 = sin0 + Ceos 0, откуда С= 1. Таким образом, искомое частное решение имеет вид }> = sin*+cos*. ф Найдите общие решения уравнений: 26. 1) ^-2j-3=0; 2) ^=у+1; 3) x^f-x2 + 2y=0. dx dx dx 27. 1) %+ху=х; 2) 3) %-ус Цдг-йп*. Найдите частные решения уравнений, удовлетворяющие указанным начальным условиям:
§4. НЕПОЛНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА Уравнение, содержащее производные (или дифференциалы) не выше второго порядка, называется дифференциальным уравнением второго порядка. В общем виде уравнение второго порядка записывается следующим образом:
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные. 32. Найти общее решение уравнения 3 -^=sin jc.
d2y.. dy —— =f(x). Полагаем —=z; тогда данное уравнение можно записать в виде dx2 4 ' dx d (dy\ dz I — I = sm x, т. e. — =sin x, dx \dx) dx откуда dz = sin xdx. Интегрируя последнее равенство, получим J d!z = J sin jc dx, т. e. z=— cosx+C1. Следовательно, dy —-= -cosx+ Cl5 т. e. dy=(—cosx+C^dx. dx Снова интегрируя, находим jdy — j(—cosx+Cjdx, или y= — втх+С^+Сз- Это и есть общее решение данного уравнения, ф 33. Найти частное решение уравнения ^Л=2^-, если у=4 и %= 1 dx1 dx 7 2 dx при jc=0. О Это неполное дифференциальное уравнение второго порядка вида d2y J dy\ dy d2y dz dz —r=/|—. Положим =z; тогда —г=— и, значит, =2z. Разделив в dx2 \dxj dx dx2 dx dx
Следовательно, dy dx = e2^, (*) т. e. dy=e2x+c'dx. Интегрируя, находим общее решение данного уравнения: у=(\/2)е2х+с> + С2. (**) Для нахождения искомого частного решения подставим в соотношения (*) и (**) начальные данные: (\==е20+с', \3/2 = (1/2)е2 0+с> + С2, ““ |з/2=(1 (1/2) ес‘ + С2, откуда С 1=0, С2 = 1* Таким образом, искомое частное решение имеет вид у=(\/2)eix+l. ф d2y 1 dy 34. Найти частное решение уравнения —%=—- -f-, если у = 2 и dxz х+2 dx
d у dy dz 1 —г- и — в данное уравнение, получим —=----------- z. Разделив переменные и dx dx dx х+2 интегрируя, имеем dz dx Г dz Г dx —=------ \nz=\n(x+2)+\nCl, z x+2 J z J x+2 откуда z = C1(.x;+2). Следовательно, %=Ct(x+ 2 ). (*) Теперь можно найти общее решение данного уравнения: >>=(1/2) C1jc2 + 2C1x+C2. (**) Найдем частное решение, подставив в уравнения (*) и (**) начальные данные: 8 = С, (2 + 2), 2 = (1/2) С1-22 + 2С1-2 + С2, откуда Cj= 2 и С2= —10. Таким образом, искомое частное решение имеет вид у=х2 + 4х—10. # Найдите частные решения уравнений, удовлетворяющие указанным начальным условиям: 43. Ускорение свободно падающего тела удовлетворяет уравне- d2s нию -^=g (g~9,8 м/с2). Найдите закон движения тела, если s=s0 и ds —= v 0 в момент времени / = 0. dt §5. ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида d2y dy ~dS+pTx- —+p—+qy=0, (15.1) где р и q—постоянные величины. Для отыскания общего решения уравнения (15.1) составляется характеристическое уравнение r2+pr+q = О, (15.2) d2y dy которое получается из уравнения (15.1) заменой —-, — и у на соответ- dx 2 dx ствующие степени г, причем сама функция у заменяется единицей. Тогда общее решение дифференциального уравнения (15.1) строится в зависимости от корней г1 и г2 характеристического уравнения (15.2). Здесь возможны три случая. I случай. Корни rj и г2—действительные и различные. В этом случае общее решение уравнения (15.1) имеет вид у = СхеТ'х+СгеТ*. (15.3) II случай. Корни и г2—действительные и равные: r1 = r2=r. Тогда общее решение уравнения (15.1) записывается так: У={С^С2х)егх. (15.4) III случай. Корни г1 и г2—комплексно-сопряженные: г1 =а-Ьр/; г2 = а—(3/. В этом случае общее решение уравнения (15.1) записывается следующим образом: ^^(Cjcospx+Cjsinpx). (15.5) d2y - dy dx2 dx 44. Решить уравнение 7 —+ 10у = 0.
45. Найти частное решение уравнения 5 —=0, если у= 1 и О Составим характеристическое уравнение г2 — 5г=0, откуда г1 = 0, г2 = 5. Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид у = С1е0 х+С2е5х, т. е. у = С1 + С2е5х. Для нахождения искомого частного решения нужно определить значения постоянных Сх и С2. Подставив в общее решение значения *=0, у= 1, получим \ = С1 + С2. Продифференцировав общее решение и подставив в полученное выраже- dy dy ние значения *=0, —= — 1, имеем —=5С2е, —1 = 5С2. Отсюда находим: dx dx С2= —1/5, Cj = 1 — С2 = 6/5. Таким образом, искомое частное решение имеет вид у = 6/5-(l/5)eSx. Ф d2y dy 46. Решить уравнение —г—8—I-16^ = 0. dx dx О Составим характеристическое уравнение и найдем его корни: г2 — 8r+16 = 0; г1 = г2=4. Характеристическое уравнение имеет равные действительные корни; поэтому согласно формуле (15.4) общее решение данного дифференциального уравнения записывается в виде у = (С1 + С2х)е4х. ф 47. Найти частное решение уравнения у" + 8у'+16^ = 0, если у= 1 и у'= 1 при * = 0. О Так как характеристическое уравнение г2 + 8г+16 = 0 имеет равные действительные корни г1 = г2= —4, то общее решение данного дифференциального уравнения записывается в виде у = (Q + С2х) е~4х = С1е~4х+С2хе~*х. Дифференцируя общее решение, имеем /= — 4Cte ~4х + С2е ~4х—4С2хе ~ 4х. Подставив начальные данные в выражения для у и у\ получим систему уравнений Г1=С>о+С2-0-ео, fl=Clt {l = -4C1e°+C2eo-4C2 0 e°, |l = -4C1 + C2, откуда Cj = 1 и С2 = 5. Следовательно, искомое частное решение имеет вид у=е~4х+5хе~4х. ф 48. Решить уравнение у" — 6у' + 25у = 0. О Составим характеристическое уравнение и найдем его корни: г2 — 6r+25 = 0; rj = 3 + 4/, r2 = 3—4i; здесь а = 3, р=4. Так как характеристическое уравнение имеет два комплексно-сопряженных корня, то общее решение дифференциального уравнения согласно формуле (15.5) записывается в виде ^=e3x(C1cos4*+C2sin4*). • 49. Найти частное решение уравнения у" — 6у'+13 = 0, если у= 1 и / = 5 при л:=0. О Поскольку характеристическое уравнение г2 —6г+13 = 0 имеет комп- лексно-сопряженные корни ^ = 3 + 2/ и г2 = 3 — 2/, общее решение данно
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 910; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.014 с.) |

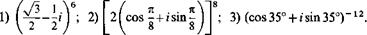
 Степень ez с комплексным показателем z=x+iy определяется равенством
Степень ez с комплексным показателем z=x+iy определяется равенством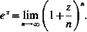
 Умножение, деление, возведение в целую положительную степень и извлечение корня целой положительной степени для комплексных чисел, заданных в показательной форме, выполняются по следующим формулам:
Умножение, деление, возведение в целую положительную степень и извлечение корня целой положительной степени для комплексных чисел, заданных в показательной форме, выполняются по следующим формулам:


 ——= Проинтегрируем полученное уравнение:
——= Проинтегрируем полученное уравнение: Отсюда находим
Отсюда находим


 Для отыскания и получаем уравнение
Для отыскания и получаем уравнение “Jtgxdx; In u = In cos*; w = cos*. Подставляя выражение для и в уравнение (*), имеем
“Jtgxdx; In u = In cos*; w = cos*. Подставляя выражение для и в уравнение (*), имеем dz
dz

 О Это неполное дифференциальное уравнение второго порядка вида
О Это неполное дифференциальное уравнение второго порядка вида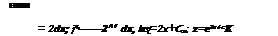 этом уравнении переменные и интегрируя, получим dz z
этом уравнении переменные и интегрируя, получим dz z
 Положим —=z; тогда =—. Подставив выражения для
Положим —=z; тогда =—. Подставив выражения для О Составим характеристическое уравнение и найдем его корни: r2-7r+10 = 0; rt = 2, г2 = 5. Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения согласно формуле (15.3) запишется так: у=Схе2х + С2е5х. #
О Составим характеристическое уравнение и найдем его корни: r2-7r+10 = 0; rt = 2, г2 = 5. Так как корни характеристического уравнения действительные и различные, то общее решение данного дифференциального уравнения согласно формуле (15.3) запишется так: у=Схе2х + С2е5х. #


