
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Инерции. Принцип эквивалентности сил инерции и гравитацииСодержание книги
Поиск на нашем сайте
Основное уравнение динамики записано выше для инерциальной системы отсчета (ИСО). В общем случае система координат может быть связана с телом отсчета, движущимся произвольно в некоторой ИСО. Для записи уравнения движения частицы относительно такой неинерциальной системы отсчета (НИСО) воспользуемся формулой сложения ускорений (теоремой Кориолиса):
Здесь сила Итак, уравнение движения в НИСО имеет вид:
Здесь Если частица в НИСО неподвижна, то Сила Кориолиса зависит не только от переносного движения, но и от относительного движения частицы в НИСО: Для тел на Земле центробежная сила инерции проявляется в зависимости ускорения свободного падения от широты местности (на экваторе величина g меньше, чем на полюсах). Сила Кориолиса отклоняет движущиеся тела (в северном полушарии любая река больше подмывает правый берег); действием силы Кориолиса объясняется своеобразное движение маятника Фуко. Совместное действие центробежной силы и силы Кориолиса отклоняет свободно падающее тело на юго-восток (в Северном полушарии) от направления к центру Земли.
Силы инерции, действующие на частицу в НИСО, по своим проявлениям не отличаются от фундаментальной силы, действующей в гравитационном поле. Это их свойство обусловлено пропорциональностью (при принятом выборе единиц измерения – равенством) инертной и гравитационной масс тела. Эта пропорциональность (равенство) для всех тел не вытекает из каких-либо положений механики, а является самостоятельным утверждением – обобщением экспериментальных фактов (опыты Галилея, Ньютона, Бесселя, Дикке, Панова и Брагинского и др.). Равенство проверено экспериментально с очень высокой степенью точности. Важнейшим следствием равенства инертной и гравитационной масс является равенство ускорений для всех тел (частиц) в данной точке гравитационного поля (ускорение не зависит от массы рассматриваемого тела). Также не зависят от массы и ускорения, вызываемые заданными силами инерции. Это приводит к утверждению о неразличимости сил инерции и сил тяготения в небольшой области пространства за небольшие промежутки времени. Данное утверждение носит название принципа эквивалентности сил инерции и гравитации: поле тяготения в небольшой области пространства и времени по своему действию тождественно действию сил инерции в ускоренной системе отсчета. Заметим, что в небольшой области пространства и времени гравитационное поле можно считать однородным и стационарным. Принцип эквивалентности сыграл фундаментальную эвристическую роль в создании общей теории относительности, в которой равноправными считаются все системы отсчета, а не только ИСО.
7 Принципы д¢Аламбера, виртуальных перемещений и д¢Аламбера-Лагранжа. Общее уравнение механики Д¢Аламбер показал, что дифференциальные уравнения движения системы частиц могут быть представлены в форме уравнений равновесия системы сил. Уравнения движение для системы из n частиц имеют вид:
Назовем векторы
д¢Аламберовыми силами инерции. Тогда
т. е. дифференциальные уравнения движения приняли вид условий равновесия сил, приложенных к частицам системы.
Принцип д¢Аламбера: если к заданным силам и реакциям связей добавить силы, равные силам инерции, то полученная система будет находиться в равновесии. Математическое выражение принципа д¢Аламбера в декартовых координатах:
Принцип д¢Аламбера открывает возможность применения к решению динамических задач специфических методов аналитической статики, что в ряде случаев упрощает решение. Введем понятия возможных, действительных и виртуальных перемещений. Возможным перемещением
Действительное перемещение
Виртуальным перемещением
Подставляя в (2.2.6), находим:
что совпадает с (2.2.6) при стационарной связи (т. е. при В математике величины вида
Вариация координаты В аналитической механике широко применяется метод варьирования как координат, так и функций координат частиц механической системы. Пусть имеется функция координат и времени
Если координаты подверглись варьированию, то новое значение функции
Разложим (2.2.11) в ряд Тейлора по степеням бесконечно малых величин
Вариация функции (т. е. её приращение, обусловленное варьированием независимых аргументов)
отличается от полного дифференциала отсутствием члена с Т. к. координаты частицы до и после перемещения должны удовлетворять уравнениям связей, то их вариации не могут быть совершенно произвольными независимыми величинами. В самом деле, если уравнение связи
то должно выполняться равенство
Тогда
т. е. одна из вариаций координат оказывается зависимой. Все сказанное выше применимо, естественно, и для системы частиц, для которой среди Вернемся к рассмотрению системы из
Здесь
Выражения вида Заметим, что введя в уравнение реакции связей, мы от системы частиц со связями перешли к системе с силами Заметим также, что
Если связи идеальные, то
(2.2.20) – условие Лагранжа, выражающее принцип виртуальных перемещений: виртуальная работа заданных сил, приложенных к системе с идеальными связями и находящейся в равновесии, равна нулю. Объединим принцип виртуальных перемещений с принципом д¢Аламбера. Для идеальных связей запишем:
Это общее уравнение механики. В любой момент времени движения механической системы с идеальными связями алгебраическая сумма виртуальных работ заданных сил и д¢Аламберовых сил инерции равна нулю – объединенный принцип д¢Аламбера–Лагранжа, который можно использовать как основную аксиому механики. В декартовых координатах общее уравнение механики:
Общее уравнение механики легко обобщается на случай неидеальных связей:
|
|||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.83.188 (0.012 с.) |

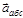 =
=  +
+  +
+  . Умножая это равенство на массу частицы и учитывая, что
. Умножая это равенство на массу частицы и учитывая, что  – ускорение частицы в ИСО (
– ускорение частицы в ИСО (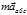 =
=  ), получим:
), получим: =
=  +(
+( )+(
)+( ). (1.8.1)
). (1.8.1)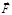 выражает действие на частицу других тел и полей и может быть указана в виде функции координат, скорости и времени:
выражает действие на частицу других тел и полей и может быть указана в виде функции координат, скорости и времени: 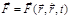 . Движение же НИСО проявилось в (1.8.1) через слагаемые
. Движение же НИСО проявилось в (1.8.1) через слагаемые  =
= 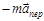 и
и  =
= 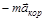 . Эти слагаемые кинематически в НИСО не могут быть обнаружены и интерпретируются как силы, приложенные к частице и вызывающие ее ускорение относительно НИСО. Таким образом, чтобы сохранить для частицы в НИСО традиционную форму основного уравнения динамики, величины
. Эти слагаемые кинематически в НИСО не могут быть обнаружены и интерпретируются как силы, приложенные к частице и вызывающие ее ускорение относительно НИСО. Таким образом, чтобы сохранить для частицы в НИСО традиционную форму основного уравнения динамики, величины  и
и  следует рассматривать как особого рода силы – силы инерции, которые не являются результатом действия каких-либо тел или полей на частицу, а представляют прямой результат неинерциальности системы отсчета.
следует рассматривать как особого рода силы – силы инерции, которые не являются результатом действия каких-либо тел или полей на частицу, а представляют прямой результат неинерциальности системы отсчета. +
+  . (1.8.2)
. (1.8.2)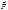 – равнодействующая всех «ньютоновских» сил, действующих на частицу,
– равнодействующая всех «ньютоновских» сил, действующих на частицу,  +
+  +
+  =
= 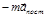

 , где
, где  – переносное поступательное ускорение,
– переносное поступательное ускорение,  – переносное вращательное ускорение,
– переносное вращательное ускорение,  =
=  =
=  – переносное центростремительное ускорение;
– переносное центростремительное ускорение;  и
и  – поступательная, вращательная и центробежная силы инерции.
– поступательная, вращательная и центробежная силы инерции. = 0,
= 0,  = 0 и
= 0 и 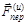 = 0. Именно такое уравнение следует применять к покоящемуся на Земле телу, причем
= 0. Именно такое уравнение следует применять к покоящемуся на Земле телу, причем  »
»  .
.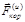 =
=  =
=  =
=  . На покоящиеся в НИСО тела сила Кориолиса не действует.
. На покоящиеся в НИСО тела сила Кориолиса не действует. , i = 1, 2, …, n (2.2.1)
, i = 1, 2, …, n (2.2.1) (2.2.2)
(2.2.2) (2.2.3)
(2.2.3) (2.2.4)
(2.2.4) называют обычно бесконечно малое перемещение частицы, совместимое с наложенными связями, т. е. удовлетворяющее уравнению связи
называют обычно бесконечно малое перемещение частицы, совместимое с наложенными связями, т. е. удовлетворяющее уравнению связи (2.2.5)
(2.2.5) – то из возможных, которое удовлетворяет уравнениям движения. Если возможное перемещение
– то из возможных, которое удовлетворяет уравнениям движения. Если возможное перемещение 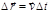 (
( и
и  – элементарно малые величины), то из известного дифференциального уравнения связи
– элементарно малые величины), то из известного дифференциального уравнения связи  для возможного перемещения получаем:
для возможного перемещения получаем: (2.2.6)
(2.2.6) называют бесконечно малое «перемещение» частицы, допускаемое связью в данный фиксированный момент времени. По сути это разность двух бесконечно близких возможных перемещений:
называют бесконечно малое «перемещение» частицы, допускаемое связью в данный фиксированный момент времени. По сути это разность двух бесконечно близких возможных перемещений: (2.2.7)
(2.2.7) (2.2.8)
(2.2.8) ) Таким образом, при стационарных связях понятия виртуального и возможного перемещений совпадают. Виртуальное перемещение не обусловлено действием сил и не обладает длительностью – это чисто геометрическое понятие, характеризующее структуру наложенных связей.
) Таким образом, при стационарных связях понятия виртуального и возможного перемещений совпадают. Виртуальное перемещение не обусловлено действием сил и не обладает длительностью – это чисто геометрическое понятие, характеризующее структуру наложенных связей. называют вариациями;
называют вариациями;  – вариация радиус-вектора частицы, причем
– вариация радиус-вектора частицы, причем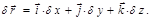 (2.2.9)
(2.2.9) – её бесконечно малое приращение, обусловленное переходом в данный момент времени от заданного движения к мысленному, допускаемому связями. Вариация отличается от бесконечно малого приращения координаты
– её бесконечно малое приращение, обусловленное переходом в данный момент времени от заданного движения к мысленному, допускаемому связями. Вариация отличается от бесконечно малого приращения координаты 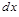 , обусловленного приращением аргумента (времени):
, обусловленного приращением аргумента (времени):  И вариация, и дифференциал – бесконечно малые изменения координаты, различные по своей природе.
И вариация, и дифференциал – бесконечно малые изменения координаты, различные по своей природе.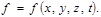 (2.2.10)
(2.2.10) (2.2.11)
(2.2.11) :
: (2.2.12)
(2.2.12) (2.2.13)
(2.2.13) .
. (2.2.14)
(2.2.14)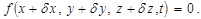 (2.2.15)
(2.2.15) (2.2.16)
(2.2.16) вариаций координат только
вариаций координат только  независимых вариаций (столько, сколько степеней свободы).
независимых вариаций (столько, сколько степеней свободы). частиц. Для её равновесия необходимо и достаточно, чтобы алгебраические суммы проекций всех сил, приложенных к каждой частице, на каждую координату были равны нулю:
частиц. Для её равновесия необходимо и достаточно, чтобы алгебраические суммы проекций всех сил, приложенных к каждой частице, на каждую координату были равны нулю: (2.2.17)
(2.2.17) – равнодействующая активных сил, приложенных к
– равнодействующая активных сил, приложенных к  -й частице,
-й частице,  – равнодействующая соответствующих реакций связей,
– равнодействующая соответствующих реакций связей,  Домножим уравнение (2.2.17) на вариации соответствующих координат и просуммируем:
Домножим уравнение (2.2.17) на вариации соответствующих координат и просуммируем: (2.2.18)
(2.2.18)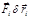 и
и 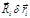 имеют смысл работы на виртуальных перемещениях и называются виртуальной работой. Итак, сумма виртуальных работ заданных (активных) сил и сил реакции для всех частиц системы, находящейся в равновесии, равна нулю.
имеют смысл работы на виртуальных перемещениях и называются виртуальной работой. Итак, сумма виртуальных работ заданных (активных) сил и сил реакции для всех частиц системы, находящейся в равновесии, равна нулю. и
и  (принцип освобождаемости от связей). При таком подходе все вариации
(принцип освобождаемости от связей). При таком подходе все вариации  независимы, и уравнения (2.2.17) и (2.2.18) эквивалентны.
независимы, и уравнения (2.2.17) и (2.2.18) эквивалентны.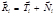 , где
, где  – силы нормальных реакций, не совершающие работы. Тогда
– силы нормальных реакций, не совершающие работы. Тогда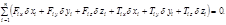 (2.2.19)
(2.2.19) (в общем случае идеальными можно называть связи, для которых виртуальная работа сил реакции обращается в нуль). В этом случае
(в общем случае идеальными можно называть связи, для которых виртуальная работа сил реакции обращается в нуль). В этом случае (2.2.20)
(2.2.20) (2.2.21)
(2.2.21) (2.2.22)
(2.2.22) (2.2.23)
(2.2.23)


