
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Гамильтона-Якоби. Теорема ЯкобиСодержание книги
Поиск на нашем сайте Наряду с обыкновенными дифференциальными уравнениями Лагранжа и Гамильтона, существует уравнение в частных производных, описывающее движение механической системы в поле обобщенно-потенциальных сил при наличии голономных идеальных связей – уравнение Гамильтона-Якоби. Ранее было показано, что и
Уравнение Гамильтона-Якоби также служит основой для некоторого общего метода интегрирования уравнений движения. Как известно, всякое дифференциальное уравнение в частных производных первого порядка имеет решение, зависящее от произвольной функции – так называемый общий интеграл уравнения. В механических применениях основную роль играет, однако, не общий интеграл уравнения Гамильтона-Якоби, а полный интеграл – решение дифференциального уравнения в частных производных, содержащее столько независимых произвольных постоянных, сколько независимых переменных в уравнении. В уравнении Гамильтона-Якоби независимые переменные
где Для выяснения связи между полным интегралом уравнения Гамильтона-Якоби и решением уравнений движения произведем каноническое преобразование от величин
Функция f удовлетворяет уравнению Гамильтона-Якоби, поэтому
и канонические уравнения в новых переменных имеют вид:
откуда С другой стороны s уравнений Изложенное выше обобщает теорема Якоби: если некоторая функция
где Первые соотношения (7.6.8) определяют обобщенные импульсы как функции координат и времени: Используя теорему Якоби, можно решить задачу о движении механической системы с обобщенно-потенциальными силами и идеальными голономными связями следующим образом: по известной функции Гамильтона составляем уравнение Гамильтона-Якоби, а затем находим полный интеграл этого уравнения вида (7.6.3) с последующим использованием уравнений (7.6.8). Если мы имеем неполный интеграл уравнения Гамильтона-Якоби, зависящий от числа произвольных постоянных меньше s, то, хотя с его помощью и нельзя найти общий интеграл уравнений движения, можно все же несколько упростить задачу его нахождения. Так, если известна функция S, содержащая одну произвольную постоянную
дает одно уравнение, связывающее Уравнение Гамильтона-Якоби упрощается для случая явной независимости H от t (например, для консервативной системы). Зависимость действия от времени сводится при этом к выражению
и для укороченного действия
Заметим, что физические допущения, лежащие в основе уравнений Гамильтона и уравнения Гамильтона-Якоби, одинаковы. Но основной метод решения уравнения Гамильтона-Якоби (метод разделения переменных) включает в себя как частный случай метод циклических координат Лагранжа, и при рассмотрении уравнения Гамильтона-Якоби наиболее естественно вскрывается достаточно глубокая аналогия между механикой частицы и волновым процессом, играющая важную роль при обсуждении волнового аспекта квантовомеханических явлений.
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 , k = 1, 2,..., s, (7.6.1)
, k = 1, 2,..., s, (7.6.1) . Заменяя в (7.6.1) импульсы производными от действия по координатам, получаем уравнение Гамильтона-Якоби, которому удовлетворяет функция действия
. Заменяя в (7.6.1) импульсы производными от действия по координатам, получаем уравнение Гамильтона-Якоби, которому удовлетворяет функция действия 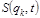 :
: , k = 1, 2,..., s, (7.6.2)
, k = 1, 2,..., s, (7.6.2) . Для системы с s степенями свободы полный интеграл этого уравнения должен содержать (s + 1) произвольных постоянных. Поскольку функция S входит в уравнение только через свои производные, то одна из произвольных постоянных содержится в полном интеграле аддитивным образом, т. е. вид полного интеграла уравнения Гамильтона-Якоби:
. Для системы с s степенями свободы полный интеграл этого уравнения должен содержать (s + 1) произвольных постоянных. Поскольку функция S входит в уравнение только через свои производные, то одна из произвольных постоянных содержится в полном интеграле аддитивным образом, т. е. вид полного интеграла уравнения Гамильтона-Якоби: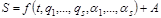 , (7.6.3)
, (7.6.3)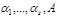 – произвольные постоянные.
– произвольные постоянные. и
и 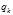 к новым переменным, причем функцию
к новым переменным, причем функцию  выберем в качестве производящей функции, а величины
выберем в качестве производящей функции, а величины  – в качестве новых импульсов. Новые координаты обозначим
– в качестве новых импульсов. Новые координаты обозначим 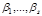 . Поскольку производящая функция зависит от старых координат и новых импульсов, используем формулы:
. Поскольку производящая функция зависит от старых координат и новых импульсов, используем формулы: (7.6.4)
(7.6.4) , (7.6.5)
, (7.6.5)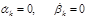 , (7.6.6)
, (7.6.6) . (7.6.7)
. (7.6.7)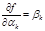 дают возможность выразить s координат
дают возможность выразить s координат  через время и 2 s постоянных
через время и 2 s постоянных  и
и 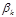 . Тем самым находится общий интеграл уравнения движения.
. Тем самым находится общий интеграл уравнения движения. является полным интегралом уравнения Гамильтона-Якоби, то решение канонических уравнений Гамильтона определяется следующими соотношениями:
является полным интегралом уравнения Гамильтона-Якоби, то решение канонических уравнений Гамильтона определяется следующими соотношениями: , k = 1, 2,..., s, (7.6.8)
, k = 1, 2,..., s, (7.6.8) и
и  – произвольные постоянные.
– произвольные постоянные. ; вторые соотношения (7.6.8) дают интегралы канонических уравнений вида
; вторые соотношения (7.6.8) дают интегралы канонических уравнений вида  , разрешая которые относительно
, разрешая которые относительно  .
.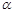 , то соотношение
, то соотношение (7.6.9)
(7.6.9)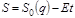 , (7.6.10)
, (7.6.10) уравнение Гамильтона-Якоби имеет вид:
уравнение Гамильтона-Якоби имеет вид: , k = 1, 2,..., s. (7.6.11)
, k = 1, 2,..., s. (7.6.11)


