
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематическое описание твердого тела. Углы ЭйлераСодержание книги
Поиск на нашем сайте
Для описания движения твердого тела введем две системы координат: «неподвижную» инерциальную Рисунок 6.1.1 Пусть радиус-вектор Таким образом, всякое твердое тело представляет собой механическую систему с шестью степенями свободы (если его движение не ограничено дополнительными условиями). Произвольное бесконечно малое перемещение твердого тела можно представить как совокупность бесконечно малого параллельного переноса системы
где
получаем соотношение между ними:
Здесь Если перенести начало 0 в другую точку С другой стороны, по определению должно быть
Последнее равенство свидетельствует о том, что угловая скорость вращения жестко связанной с телом СК не зависит от выбора этой системы. Все такие системы вращаются в данный момент времени вокруг параллельных друг другу осей с одинаковой угловой скоростью Из первой формулы (6.1.6) видно, что если
При вращении твердого тела вокруг неподвижной оси меняется только угол Рисунок 6.1.2 Кинематическое уравнение движения в этом случае
Тогда Рассмотрим более сложное движение тела относительно неподвижной точки. В механике твердого тела важное значение имеет теорема Эйлера: всякое мгновенное движение твердого тела можно представить как результат мгновенного поступательного движения произвольно выбранной точки и мгновенного вращательного движения вокруг мгновенной оси вращения, проходящей через эту точку. Собственно, об этом уже было сказано выше, только другими словами. Из теоремы Эйлера следует, что в любой момент времени в теле можно провести прямую, проходящую через неподвижную точку так, что все точки прямой в этот момент времени неподвижны, т. е. прямая – мгновенная ось вращения. Целесообразно поэтому совместить с неподвижной точкой начала обеих СК (неподвижной и жестко связанной с телом подвижной) и рассматривать вращательное движение подвижной СК с угловой скоростью Пусть Скорость любой точки твердого тела Тогда Формулы (6.1.10) применимы и при движении начала подвижной СК. Таким образом, если известны координаты твердого тела в СК, связанной с ним, и проекции угловой скорости на оси этой СК, то можно вычислить скорость рассматриваемой точки. Для нахождения величин
Угол прецессии Рисунок 6.1.3 Прямая
Считая эти уравнения известными, найдем
где Последнее очевидно из взаимного расположения векторов
Несложно убедиться, что
Здесь учтено, что
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 687; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 Твердое тело можно определить в механике как непрерывную систему материальных точек, расстояния между которыми неизменны (это модель, абстракция). Непрерывность тела предполагает рассмотрение не отдельной материальной точки массой
Твердое тело можно определить в механике как непрерывную систему материальных точек, расстояния между которыми неизменны (это модель, абстракция). Непрерывность тела предполагает рассмотрение не отдельной материальной точки массой  , а элемента объема
, а элемента объема  массой
массой  , что заменяет операцию суммирования интегрированием по объему (или массе) тела.
, что заменяет операцию суммирования интегрированием по объему (или массе) тела. и движущуюся
и движущуюся  , которая предполагается жестко связанной с телом и участвующей во всех его движениях (рисунок 6.1.1). Начало 0 движущейся СК удобно совместить с центром инерции тела. Положение твердого тела относительно неподвижной СК вполне определяется заданием положения подвижной СК.
, которая предполагается жестко связанной с телом и участвующей во всех его движениях (рисунок 6.1.1). Начало 0 движущейся СК удобно совместить с центром инерции тела. Положение твердого тела относительно неподвижной СК вполне определяется заданием положения подвижной СК. указывает положение начала 0 движущейся СК. Ориентация осей последней относительно неподвижной СК определяется тремя независимыми углами, которые с тремя компонентами вектора
указывает положение начала 0 движущейся СК. Ориентация осей последней относительно неподвижной СК определяется тремя независимыми углами, которые с тремя компонентами вектора  дают шесть независимых координат.
дают шесть независимых координат. (перемещение центра инерции) и бесконечно малого поворота системы
(перемещение центра инерции) и бесконечно малого поворота системы  , (6.1.1)
, (6.1.1) и
и  – элементарные приращения (изменения) векторов
– элементарные приращения (изменения) векторов  и
и  – вектор, модуль которого численно равен углу поворота СК системы
– вектор, модуль которого численно равен углу поворота СК системы  , неподвижного относительно этой СК) относительно перпендикулярной плоскости угла
, неподвижного относительно этой СК) относительно перпендикулярной плоскости угла  оси, проходящей через точку 0. Вводя скорости:
оси, проходящей через точку 0. Вводя скорости: ,
,  ,
, 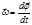 , (6.1.2)
, (6.1.2) . (6.1.3)
. (6.1.3) – скорость т. 0 относительно т.
– скорость т. 0 относительно т.  (скорость поступательного движения твердого тела),
(скорость поступательного движения твердого тела),  – угловая скорость вращения твердого тела,
– угловая скорость вращения твердого тела,  – скорость сложного движения определенной фиксированной точки тела.
– скорость сложного движения определенной фиксированной точки тела. твердого тела так, что
твердого тела так, что 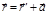 , то
, то  . (6.1.4)
. (6.1.4) . (6.1.Отсюда заключаем, что
. (6.1.Отсюда заключаем, что ,
,  . (6.1.6)
. (6.1.6) . Поэтому можно называть величину
. Поэтому можно называть величину  и
и  в данный момент времени взаимно перпендикулярны при каком-либо выборе начала координат 0, то они (т. е.
в данный момент времени взаимно перпендикулярны при каком-либо выборе начала координат 0, то они (т. е.  и
и  ) взаимно перпендикулярны и при любом другом начале координат
) взаимно перпендикулярны и при любом другом начале координат  . Из (6.1.3) видно, что в этом случае скорости
. Из (6.1.3) видно, что в этом случае скорости  . При этом всегда можно выбрать такое начало
. При этом всегда можно выбрать такое начало  (возможно и вне тела), скорость которого
(возможно и вне тела), скорость которого  в данный момент времени. Тогда движение твердого тела в данный момент может быть представлено как чистое вращение вокруг оси, проходящей через т.
в данный момент времени. Тогда движение твердого тела в данный момент может быть представлено как чистое вращение вокруг оси, проходящей через т.  В общем случае не взаимно перпендикулярных направлений
В общем случае не взаимно перпендикулярных направлений  начало координат можно выбрать так, чтобы
начало координат можно выбрать так, чтобы 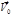 и
и  стали параллельными, т. е. движение в данный момент времени будет совокупностью вращения вокруг некоторой оси и поступательного движения вдоль нее же. При движении тела могут, вообще говоря, меняться как модуль вектора
стали параллельными, т. е. движение в данный момент времени будет совокупностью вращения вокруг некоторой оси и поступательного движения вдоль нее же. При движении тела могут, вообще говоря, меняться как модуль вектора  , так и направление оси вращения.
, так и направление оси вращения. – тело имеет одну степень свободы (рисунок 6.1.2).
– тело имеет одну степень свободы (рисунок 6.1.2). . (6.1.7)
. (6.1.7)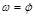 ,
,  , угловое ускорение
, угловое ускорение  . Для определенной точки тела (для элемента массы
. Для определенной точки тела (для элемента массы  ) тангенциальное ускорение
) тангенциальное ускорение  , нормальное ускорение
, нормальное ускорение  .
. – неподвижная СК,
– неподвижная СК, 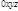 – подвижная СК с ортами
– подвижная СК с ортами  (рисунок 6.1.1).
(рисунок 6.1.1). . (6.1.8)
. (6.1.8) =
=  . (6.1.9)Отсюда
. (6.1.9)Отсюда  (6.1.10)
(6.1.10) нужно знать закон движения СК
нужно знать закон движения СК  , т. е. зависимость от времени трех угловых координат, характеризующих вращение подвижной СК. Наиболее удобны в этом плане углы Эйлера (рисунок 6.1.3).
, т. е. зависимость от времени трех угловых координат, характеризующих вращение подвижной СК. Наиболее удобны в этом плане углы Эйлера (рисунок 6.1.3).
 (плоскость угла перпендикулярна оси
(плоскость угла перпендикулярна оси  ) меняется при повороте СК
) меняется при повороте СК  (плоскость угла перпендикулярна оси
(плоскость угла перпендикулярна оси  ) меняется при повороте СК
) меняется при повороте СК  относительно оси
относительно оси  . Угол нутации
. Угол нутации  – угол между осями
– угол между осями  и
и  . Углы Эйлера независимы и могут служить угловыми координатами, характеризующими вращательное движение СК
. Углы Эйлера независимы и могут служить угловыми координатами, характеризующими вращательное движение СК  относительно СК
относительно СК  .
. – линия узлов – линия пересечения координатных плоскостей
– линия узлов – линия пересечения координатных плоскостей  и
и  . Кинематические уравнения движения:
. Кинематические уравнения движения: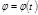 ,
,  ,
,  . (6.1.11)
. (6.1.11) . Представим вектор угловой скорости как сумму трех векторов:
. Представим вектор угловой скорости как сумму трех векторов: , (6.1.12)
, (6.1.12) ,
, 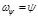 ,
,  . (6.1.13)
. (6.1.13) , каждый из которых характеризует быстроту изменения соответствующего угла Эйлера. Тогда
, каждый из которых характеризует быстроту изменения соответствующего угла Эйлера. Тогда (6.1.14)
(6.1.14)
 ...
...  (6.1.15)
(6.1.15) – проекция вектора
– проекция вектора  на плоскость
на плоскость 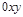 . Подставляя (6.1.15) в (6.1.14) с учетом (6.1.13), получаем кинематические формулы Эйлера:
. Подставляя (6.1.15) в (6.1.14) с учетом (6.1.13), получаем кинематические формулы Эйлера: (6.1.16)
(6.1.16)


