
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа 7. Определение момента инерции твердых тел с помощью маятника максвеллаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы - изучение маятника Максвелла и определение с его помощью момента инерции твердых тел.
Теоретические основы лабораторной работы
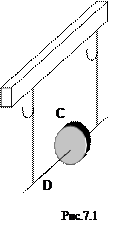
Маятник Максвелла представляет собой однородный диск С, через центр которого проходит металлический стержень D (рис.7.1). К концам этого стержня прикреплены две нити. Они тщательно, виток к витку, наматываются на стержень в направлении от его конца к диску. При этом диск на стержне поднимается вверх. Если не удерживать диск в верхнем положении, то возникает поступательное движение маятника вниз и его вращательное движение вокруг оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нити на стержень. Диск снова поднимается вверх и движение повторяется, т.е. возникают колебания. Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Момент инерции тела величина аддитивная. Если мысленно представить тело состоящим из большого число весьма малых элементов D mi, то момент инерции такого дискретного тела приближённо определяется по формуле
Приближение тем точнее, чем больше количество разбиений тела на элементарные массы D mi. При бесконечно большом значении числа элементарных масс i стремится к бесконечности, а D mi. стремится к нулю. Тогда момент инерции сплошного твёрдого тела (непрерывное распределение масс) определяется по формуле
где ri - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции различных тел сводится к интегрированию по формуле (7.1) для соответствующего объёма тела. При выводе расчётных формул использованы соотношения для моментов инерции тел, и закон сохранения полной механической энергии. Учитывая, что момент инерции тела величина аддитивная, теоретическое значение момента инерции маятника Максвелла J т можно определить в виде суммы моментов инерции, полученных как результат интегрирования по формуле (7.1) для его трёх элементов: оси маятника, диска и кольца, надетого на диск
В формуле (7.2): момент инерции оси маятника момент инерции диска момент инерции кольца, надетого на диск здесь R о, m 0, R д, m д, R к, m к - соответственно радиусы и массы оси, диска и кольца. Кинетическая энергия маятника массой m, поднятого и зафиксированного на высоте h, равна нулю. Полная механическая энергия определяется только потенциальной энергией E п = mgh. В нижнем положении маятника E п = 0, и полная механическая энергия равна сумме кинетических энергий поступательного
При таком движении модуль угловой скорости w, модуль линейной скорости u и радиус диска R связаны соотношением
Из закона сохранения следует, что полная энергия маятника в верхнем и нижнем положениях должна быть одинакова, т.е.
Отсюда, учитывая соотношение (4), момент инерции маятника
Для равнопеременного движения связь между расстоянием h, пройденным телом, величиной скорости u и временем t имеет вид
Подставляя последнее выражение в формулу (7.6), получим зависимость для определения экспериментального значения момента инерции
Формулу (7.8) можно вывести и на основе уравнений динамики для поступательного и вращательного движения (см. лаб. работа 5).
Описание установки
Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на двух нитях 4 (бифилярный подвес). На диск можно насаживать сменные кольца 12, изменяя, таким образом, момент инерции системы. Маятник удерживается в верхнем положении электромагнитом 10. Фотоэлектрические датчики 3 и 11 соединены с электронным секундомером 2. Верхний электронный датчик фиксирует момент начала движения маятника, а нижний - окончания движения (опускания) маятника. Порядок выполнения работы
8. Повторить пп.1-7 еще десять раз.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.159.163 (0.006 с.) |

 В данной лабораторной работе момент инерции твёрдых тел определяется экспериментально с помощью маятника Максвелла.
В данной лабораторной работе момент инерции твёрдых тел определяется экспериментально с помощью маятника Максвелла.
 =
= 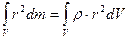 (7.1)
(7.1) (7.2)
(7.2) ;
;
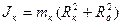 ;
; и вращательного
и вращательного  движений
движений (7.3)
(7.3) (7.4)
(7.4) (7.5)
(7.5) (7.6)
(7.6)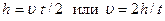 (7.7)
(7.7) (7.8)
(7.8)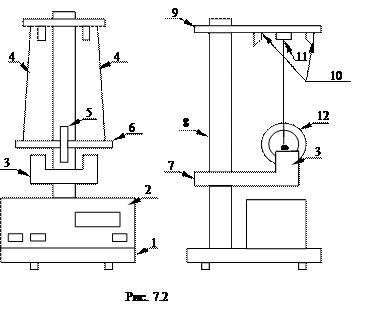 Общий вид установки представлен на рис.7.2. В основании 1 закреплена колонка с электронным секундомером 2, к которой прикреплен неподвижно верхний кронштейн 9 и подвижный нижний кронштейн 7. На верхнем кронштейне находится электромагнит 10 и фотоэлектрический датчик 11, а на нижнем кронштейне – фотоэлектронный датчик 3.
Общий вид установки представлен на рис.7.2. В основании 1 закреплена колонка с электронным секундомером 2, к которой прикреплен неподвижно верхний кронштейн 9 и подвижный нижний кронштейн 7. На верхнем кронштейне находится электромагнит 10 и фотоэлектрический датчик 11, а на нижнем кронштейне – фотоэлектронный датчик 3.


