
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 15. Физический и математический маятникСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
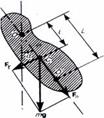
Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела (рисунок 1.55).
Рисунок 1.55 Если маятник отклонен из положения равновесия на некоторый угол α, то в соответствии с уравнением динамики вращательного движения твердого тела (1.48) момент М возвращающей силы можно записать в виде
где J – момент инерции маятника относительно оси, проходящей через точку подвеса О, l – расстояние между ней и центром масс маятника, Ft= -mgsina ≈ -mga – возвращающая сила (знак минус обусловлен тем, что направления Ft и a всегда противоположны; sinα ≈ α соответствует малым колебаниям маятника, т. е. малым отклонениям маятника из положения равновесия). Уравнение (1.106) можно записать в виде
или
Принимая
получим уравнение
идентичное с (1.100), решение которого (1.81) известно:
Из выражения (1.111) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 (см. (1.109)) и периодом
где L=J/(ml) – приведенная длина физического маятника. Точка О' на продолжении прямой ОС, отстоящая от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рисунок 1.55). Применяя теорему Штейнера (1.44), получим
т. е. OO' всегда больше ОС. Точка подвеса О маятника и центр качаний О' обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса станет новым центром качаний, и период колебаний физического маятника не изменится. 3. Математический маятник – это идеализированная система, состоящая из материальной точки массой т, подвешенной на невесомой нерастяжимой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника
где / – длина маятника. Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся его масса сосредоточена в одной точке – центре масс, то, подставив выражение (1.114) в формулу (1.112), получим выражение для периода малых колебаний математического маятника
Сравнивая формулы (1.112) и (1.115), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника. Вопрос 16 Идеальный газ Для вывода основного уравнения молекулярно-кинетической теории рассмотрим идеальный одноатомный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку S (рисунок 2.5) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс
где m0 – масса молекулы, v – ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой v t (рисунок 2.5). Число этих молекул равно n Sv t (n – концентрация молекул). Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул. Половина этих молекул (т.е. 1/6 часть) движется вдоль данного направления в одну сторону, а вторая половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет 1/6 n Sv t. При столкновении с площадкой эти молекулы передадут ей импульс
Тогда давление газа, оказываемое им на стенку сосуда,
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2,..., vN, то целесообразно рассматривать среднюю квадратичную скорость
характеризующую всю совокупность молекул газа. Уравнение (2.23) с учетом (2.24) примет вид
Выражение (2.25) называется основным уравнением молекулярно-кинетической теории идеальных газов.
Уравнению удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона – Менделеева. В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;2) между молекулами газа отсутствуют силы взаимодействия;3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно использовать при изучении реальных газов в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |



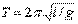
 ,
,



