
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ускорения силы тяжести оборотным маятникомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: изучение гармонических колебаний на примере колебаний физического маятника. Задачи работы: экспериментально определить ускорение силы тяжести. Приборы и принадлежности: оборотный маятник, секундомер, линейка, опорная призма.
Теория метода и описание установки Оборотный маятник представляет собой физический маятник. Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести относительно горизонтальной оси, не проходящей через его центр тяжести. Докажем, что при небольших углах отклонения
О
С
На маятник действует сила тяжести
Момент этой силы относительно оси, проходящей через точку О равен:
где
Вращающий момент
где
Приравнивая правые части уравнений (1) и (2), получим:
или, так как угол
Уравнение (3) является дифференциальным уравнением колебаний физического маятника. Сравнив это уравнение (3) с дифференциальным уравнением гармонических колебаний Т.е. физический маятник совершает гармонические колебания, и период Т колебаний его можно определить по формуле:
где
Величину Момент инерции
где
Подставив (5) в (4), получим:
Прибор состоит из горизонтальной планки, прикрепленной к стене. Наверху планки находится подушка ножевых опор для установки физического маятника. Оборотный маятник представляет собой цилиндрический стержень, на котором закреплены две треугольные ножевые опоры (опорные призмы
Выполним математические преобразования:
Вычтем из первого уравнение второе:
Отсюда найдем ускорение силы тяжести
Так как
Порядок выполнения работы 1. Подвесить маятник на призму 2. Снять маятник и подвесить на призму 3. Определить периоды 4. Определить центр тяжести маятника и измерить расстояния 5. По формуле (7) рассчитать ускорение силы тяжести. 6. Повторить опыты, смещая одну из чечевиц на 2 – 3 см. 7. Результаты измерений и вычислений занести в таблицу.
Контрольные вопросы 1. Что называется физическим маятником? 2. Запишите дифференциальное уравнение колебаний физического маятника. 3. Запишите формулу для периода колебаний физического маятника. 4. Что называется приведенной длиной физического маятника? 5. От чего зависит ускорение силы тяжести?
Литература 1. Яворский Б.М., Детлаф А.А. и др. Курс физики, т.1. 2. Шубин А.С. Курс общей физики. 3. Савельев И.В. Курс общей физики, т.1. 4. Зисман Г.А., Тодес О.М. Курс общей физики, т.1.
ЛАБОРАТОРНАЯ РАБОТА № 3 ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 759; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.143 (0.006 с.) |

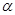 от положения равновесия физический маятник будет совершать гармонические колебания.
от положения равновесия физический маятник будет совершать гармонические колебания.




 разложим на две составляющие, одна из которых
разложим на две составляющие, одна из которых  маятник совершает колебания.
маятник совершает колебания. , (1)
, (1) - расстояние от оси качания до центра тяжести.
- расстояние от оси качания до центра тяжести. в соответствии с основным уравнением динамики вращательного движения равен:
в соответствии с основным уравнением динамики вращательного движения равен: , (2)
, (2) - момент инерции маятника;
- момент инерции маятника;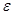 - угловое ускорение.
- угловое ускорение.
 ,
,
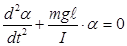 (3)
(3) , видим, что если заменить
, видим, что если заменить  и обозначить
и обозначить  , то они совпадают.
, то они совпадают. , (4)
, (4) - масса маятника.
- масса маятника. называют приведенной длиной физического маятника. Под приведенной длиной физического маятника понимают длину такого математического маятника, период колебаний которого равен периоду колебаний физического маятника.
называют приведенной длиной физического маятника. Под приведенной длиной физического маятника понимают длину такого математического маятника, период колебаний которого равен периоду колебаний физического маятника. , (5)
, (5) - момент инерции маятника относительно оси, проходящей через центр тяжести.
- момент инерции маятника относительно оси, проходящей через центр тяжести. (6)
(6) и
и  ) и две массивные чечевицы
) и две массивные чечевицы 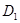 и
и  , которые можно смещать.
, которые можно смещать. Подвешивая маятник поочередно на призмы
Подвешивая маятник поочередно на призмы 
 и
и  :
: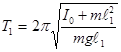




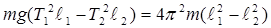
 :
:
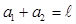 - расстояние между опорными призмами, последнюю формулу можно переписать в виде:
- расстояние между опорными призмами, последнюю формулу можно переписать в виде: (7)
(7) 100 полных колебаний маятника.
100 полных колебаний маятника.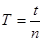 .
. и
и  .
.

















 3
3




