Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование переходных процессовСодержание книги Поиск на нашем сайте
ПРИ РАЗРЯДЕ КОНДЕНСАТОРА Цель работы: ознакомиться с процессом разряда конденсатора в различных цепях с разными параметрами. Задачи работы: 1. Определить постоянную времени 2. Определить период Т, частоту собственных колебаний напряжения и коэффициент затухания колебаний.
Приборы и принадлежности: электронный осциллограф, батарея аккумуляторов (12 В), магазин сопротивлений, батарея конденсаторов, поляризационное реле, катушка индуктивности, ключ, соединительные провода.
Теоретическое введение Разряд конденсатора через сопротивление Рассмотрим электрическую цепь, состоящую из конденсатора емкостью С и сопротивления R, соединенных с источником тока как показано на рис. 1.
С R Е
Рис. 1
С помощью ключа К конденсатор присоединяется к источнику напряжения и заряжается. Обозначим напряжение на обкладках конденсатора Такой процесс, когда при замыкании цепи величина тока устанавливается не сразу, а постепенно, называется переходным. Запишем второй закон Кирхгофа для цепи, содержащей конденсатор С и сопротивление R:
Так как Подставив выражение (2) в уравнение (1), получим дифференциальное уравнение первого порядка:
Решение этого уравнение имеет вид:
где
Тогда уравнение (4) перепишется:
Уравнение (5) выражает закон изменения напряжения со временем на обкладках конденсатора при его разряде. Выясним физический смысл постоянной Следовательно, постоянная времени Величина, обратная Коэффициент затухания
Разряд конденсатора в цепи, состоящей из сопротивления И катушки индуктивности На рис. 2 изображена схема электрической цепи, состоящей из конденсатора С, сопротивления R и катушки индуктивности L. Соединив ключом клеммы 1 – 3, зарядим конденсатор до напряжения
L
Е С
R
Рис. 2
Запишем второй закон Кирхгофа для данной цепи:
Заменив в этом уравнении
Решение этого уравнения имеет вид:
График этой функции имеет вид:
Анализируя это выражение, можно прийти к следующим заключениям: 1. При разряде конденсатора в цепи, содержащей R, L и C, величина напряжения на обкладках конденсатора совершает затухающие колебания. 2. Величина 3. Амплитуда затухающих колебаний напряжения изменяется по закону 4. Циклическая частота 5. Период затухающих колебаний:
С увеличением сопротивления R контура период Т возрастает, а при Если Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим. Значение критического сопротивления определяется условием: Если Затухание колебаний принято характеризовать логарифмическим декрементом затухания
Логарифмический декремент затухания обратен по величине числу колебаний N, совершенных за время, в течение которого амплитуда уменьшится в
Если вторичное измерение амплитуды напряжения производится через
Задание 1.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.145 (0.006 с.) |

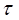 и емкость С конденсатора.
и емкость С конденсатора. 1 К 2
1 К 2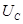 . Если теперь ключ К повернуть в положение (2), то конденсатор начнет разряжаться через сопротивление R, напряжение на обкладках конденсатора постепенно спадает до нуля. Ток в цепи, начиная от нуля, быстро достигает максимального значения
. Если теперь ключ К повернуть в положение (2), то конденсатор начнет разряжаться через сопротивление R, напряжение на обкладках конденсатора постепенно спадает до нуля. Ток в цепи, начиная от нуля, быстро достигает максимального значения  , а затем уменьшается до нуля. Весь этот процесс длится небольшой промежуток времени (доли секунды), величина которого зависит от величины сопротивления R и емкости C конденсатора.
, а затем уменьшается до нуля. Весь этот процесс длится небольшой промежуток времени (доли секунды), величина которого зависит от величины сопротивления R и емкости C конденсатора.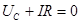 (1)
(1) , а
, а 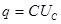 , то
, то 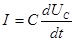 (2)
(2)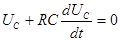 или
или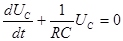 (3)
(3)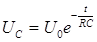 , (4)
, (4)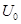 - напряжение на обкладках конденсатора в начальный момент времени (
- напряжение на обкладках конденсатора в начальный момент времени (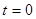 ). Произведение
). Произведение 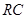 , стоящее в показателе степени имеет размерность времени и называется постоянной времени цепи с
, стоящее в показателе степени имеет размерность времени и называется постоянной времени цепи с  и С, обозначается
и С, обозначается 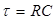
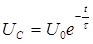 (5)
(5)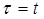 , то
, то 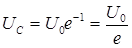 или
или  .
.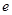 раз.
раз. называется коэффициентом затухания.
называется коэффициентом затухания.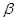 характеризует скорость уменьшения напряжения при разряде конденсатора. Чем больше R и С, тем меньше
характеризует скорость уменьшения напряжения при разряде конденсатора. Чем больше R и С, тем меньше  , т.е. тем медленнее происходит разряд конденсатора.
, т.е. тем медленнее происходит разряд конденсатора.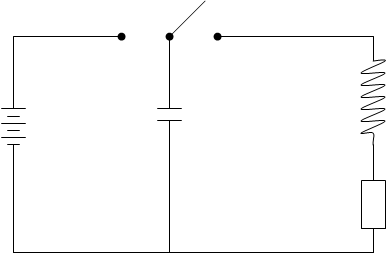 1 2
1 2
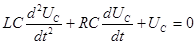 (6)
(6)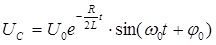 (7)
(7)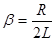 называется коэффициентом затухания.
называется коэффициентом затухания.
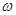 затухающих колебаний меньше собственной частоты
затухающих колебаний меньше собственной частоты 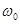 и равна:
и равна: 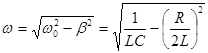
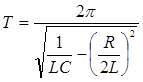
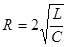 обращается в бесконечность.
обращается в бесконечность. , то изменение напряжения на обкладках не носит колебательный характер, и напряжение монотонно уменьшается до нуля. Такой разряд конденсатора называется апериодическим, т.к. в этом переходном процессе не происходит перезарядки конденсатора.
, то изменение напряжения на обкладках не носит колебательный характер, и напряжение монотонно уменьшается до нуля. Такой разряд конденсатора называется апериодическим, т.к. в этом переходном процессе не происходит перезарядки конденсатора.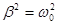 , т.е.
, т.е. 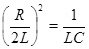 , отсюда
, отсюда 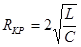
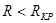 , то разряд конденсатора в цепи будет представлять собой колебательный процесс, связанный с периодической перезарядкой пластин конденсатора. Как величина напряжения на конденсаторе, так и величина тока в цепи будут совершать затухающие колебания.
, то разряд конденсатора в цепи будет представлять собой колебательный процесс, связанный с периодической перезарядкой пластин конденсатора. Как величина напряжения на конденсаторе, так и величина тока в цепи будут совершать затухающие колебания.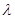 . Логарифмический декремент затухания равен натуральному логарифму отношения амплитуд двух колебаний, измеренных через промежуток времени, равный периоду Т:
. Логарифмический декремент затухания равен натуральному логарифму отношения амплитуд двух колебаний, измеренных через промежуток времени, равный периоду Т: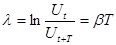
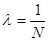
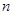 периодов после первого измерения, то
периодов после первого измерения, то