
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический и математический маятникСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
(26)
(27)
Из сравнения формул (26) и (27) следует, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Для малых колебаний математического маятника второй закон Ньютона записывается в виде Таким образом, тангенциальное ускорение aτ маятника пропорционально его смещению x, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты: Эта формула выражает собственную частоту малых колебаний математического маятника. Следовательно, Физический маятник Физический маятник ‑ это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку A, не совпадающую с центром масс С тела. Если маятник отклонен на угол α, то момент возвращающей силы можно записать в виде (22) где J ‑ момент инерции маятника, относительно оси, проходящей через точку подвеса A, l ‑ расстояние от точки A до центра масс маятника, возвращающая сила. Упругие и неупругие столкновения Процессы столкновения делятся на упругие и неупругие в соответствии с характером изменения внутренней энергии частиц при их взаимодействии. Если внутренняя энергия частиц при этом изменяется, то столкновение называется неупругим, если не изменяется - упругим.
Потенциальная энергия тел, находящихся в поле тяготения. Потенциальная энергия ‑ механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Пусть взаимодействие осуществляется посредством силовых полей. Если работа по перемещению тела во внешнем поле зависит только от начального и конечного положения тела, но не зависит от траектории, то поле потенциальное, а силы ‑ консервативные. Если работа зависит от траектории движения тела ‑ сила диссипативная. Пример диссипативной силы ‑ сила трения.
В выражении использован знак «-», т.к. работа совершается за счет убыли потенциальной энергии.
Уравнения плоской и сферической волн. Волновое уравнение. Уравнение плоской волны
Волновое уравнение
,где -оператор Лапласа
и
Энергия упругой волны. Вектор Умова-Пойтинга.
Вектор Умова-Пойтинга
Из формулы видно, что среднее значение потока энергии пропорционально значению площади ΔS. Поэтому вводят плотность среднего значения потока энергии, или коротко, интенсивность I волны, которая численно равна потоку энергии через единичную площадку, т.е.
- вектор Умова-Пойтинга, т.к. впервые введен профессором Московского университета Умовым (1845 – 1915) и профессором университета Бирмингема Пойтингом (John Henry Poynting 1852-1914).
Формула Пуазейля.
Приборы, служащие для определения вязкости по этому методу, называются вискозиметрами.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.27.41 (0.007 с.) |

 Математический маятник ‑ это идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой, невесомой нити, и колеблющаяся под действием силы тяжести. Математический маятник –это частный случай физического маятника. Хорошее приближение – тяжелый шарик на тонкой нити. Момент инерции математического маятника
Математический маятник ‑ это идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой, невесомой нити, и колеблющаяся под действием силы тяжести. Математический маятник –это частный случай физического маятника. Хорошее приближение – тяжелый шарик на тонкой нити. Момент инерции математического маятника где l ‑ длина маятника. Период колебаний математического маятника задается выражением:
где l ‑ длина маятника. Период колебаний математического маятника задается выражением: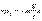
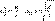


 Работа консервативных сил при бесконечно малом изменении системы равна изменению потенциальной энергии
Работа консервативных сил при бесконечно малом изменении системы равна изменению потенциальной энергии
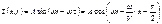
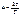 Это уравнение показывает, что колебательный процесс в упругой среде является периодическим не только во времени, но и в пространстве при изменении координаты x и фиксированном моменте времени t (рис.)
Это уравнение показывает, что колебательный процесс в упругой среде является периодическим не только во времени, но и в пространстве при изменении координаты x и фиксированном моменте времени t (рис.)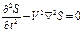 Волновое уравнение
Волновое уравнение
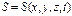
 Энергия упругой волны
Энергия упругой волны

 Т.к. скорость есть вектор, то плотность потока энергии следует также рассматривать как вектор, который направлен по скорости распространения волны
Т.к. скорость есть вектор, то плотность потока энергии следует также рассматривать как вектор, который направлен по скорости распространения волны Формула Пуазейля используется при определении коэффициента η для вязких сред путем измерения объема V вытекшей жидкости за некоторое время t при заданном перепаде давлений Δ р=р1 —р2
Формула Пуазейля используется при определении коэффициента η для вязких сред путем измерения объема V вытекшей жидкости за некоторое время t при заданном перепаде давлений Δ р=р1 —р2


