
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Бернулли и её следствия.Содержание книги
Поиск на нашем сайте
30-31 Сложение гармонических колебаний одинаковой частоты. x1=A1cos(wt+j1), x2=A2cos(wt+j2). Представим в комплексной форме: x=x1+x2=A1ei(wt+j1)+ A2ei(wt+j2)=eiwt(A1eij1+A2eij2), A1eij1+A2eij2=Aeij, A2=A12+A22+2 A1A2cos(j1–j2,), tg j=(A1sinj1+A2sinj2)/(A1cosj1+A2cosj2) Þ x=x1+x2=Aei(wt+j) Þ x=Acos(w t–j). Сложения гармонических колебаний с близкими частотами. x1=A1cos(w1t+j1), x2=A2cos(w2t+j2). Каждое из колебаний представим в комплексной форме, а сложение будем производить векторно. Пусть A1>A2. Cуммой двух колебаний с близкими частотами является колебание с изменяющейся амплитудой (от А1–А2 до А1+А2) и с частотой |w1–w2|. Колебания амплитуды с частотой W=|w1–w2| называются с биениями, а частота W – частотой биения. Законы Кеплера и закон всемирного тяготения. Первый закон Кеплера (1609 г.): Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце. Второй закон Кеплера (1609 г.): Радиус-вектор планеты описывает в равные промежутки времени равные площади. Третий закон Кеплера (1619 г.): Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит. Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью выше 1 %. Закон всемирного тяготения
47. Движение тел в поле центральных гравитационных сил. Константы (интегралы) движения. Связь момента импульса материальной точки с секториальной скоростью.Любые два тела (материальные точки) притягиваются друг к другу с силами, пропорциональными произведению их масс и обратно пропорциональными квадрату расстояния между ними. Такие силы называются гравитационными или силами всемирного тяготения. F=GMm/R2. Принцип суперпозиции гравитационных полей: гравитационное поле, возбуждаемое какой-либо массой, совершенно не зависит от наличия других масс. Гравитационное поле, создаваемое несколькими телами, равно геометрической сумме гравитационных полей, возбуждаемых этими телами в отдельности. Момент импульса, в частности, сохраняется для замкнутой системы материальных точек. Особый интерес представляют случаи центральных сил – их линии действия проходят через начало и, следовательно, суммарный момент относительно начала равен нулю, а следовательно, L=const. S’=sigma – секториальная скорость. L=m[rv]=const. |[rv]|dt=rv sin f dt=2*1/2 rv sin f dt=2dS.dS/dt=|L|/2m. sigma=|L|/2m.
Космические скорости
Условие неразрывности струи утверждает, что при ламинарном течении жидкости произведение площади сечения участка, через который она протекает, на ее скорость является постоянной величиной для данной трубки тока.Sv = const. При описании физических законов течения крови по сосудам вводится допущение, что количество циркулирующей крови в организме постоянно. Отсюда следует формулировка условия неразрывности струи для реальной гемодинамики:В любом сечении сердечно-сосудистой системы объемная скорость. кровотока постоянна:Q = const.Под площадью сечения сосудистой системы понимают суммарную площадь сечения кровеносных сосудов одного уровня ветвления. Например, в большом круге кровообращения первое (наименьшее по площади) сечение проходит через аорту, второе - через все артерии, на которые непосредственно разветвляется аорта, и т.д. Наибольшую площадь имеет сечение, соответствующее капиллярной сети.Из условия неразрывности струи следует,что с увеличением площади сечения сосудистой системы скорость кровотока в ее соответствующих участках уменьшается.
36. Скорость распостранения волн
Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле: где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.
33. Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так: , или Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.009 с.) |


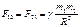 Между двумя телами, массы которых равны m1 и m2, находящимися на расстоянии R друг от друга, действуют силы взаимного притяжения и, направленные от одного тела к другому, причем величина силы тяготения пропорциональна произведению масс обоих тел и обратно пропорциональна квадрату расстояния между ними:
Между двумя телами, массы которых равны m1 и m2, находящимися на расстоянии R друг от друга, действуют силы взаимного притяжения и, направленные от одного тела к другому, причем величина силы тяготения пропорциональна произведению масс обоих тел и обратно пропорциональна квадрату расстояния между ними:



 , а поперечной:
, а поперечной: 
 , т.е.
, т.е.
 . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой.
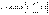 .
.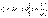 .
.


