
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы описания движения М.Т.Содержание книги
Поиск на нашем сайте
Способы описания движения М.Т. Векторный При таком способе описания движения на теле отсчета выбирается точка О (начало отсчета), из которой в направлении движущейся точки М проводят радиус-вектор (рис.). При движении точки М значение и направление радиуса-вектора r изменяются, т. е. он является функцией времени. Если вид функции r = r (t) известен, то уравнение движения точки М задано в векторной форме. Конец радиуса-вектора r (t) описывает в пространстве кривую, которая называется траекторией движущейся точки. Координатный В этом случае с телом отсчета связывается система координат, которая позволяет каждой точке пространства сопоставить три числа, называемые координатами точки этого пространства. Наиболее распространенными системами являются прямоугольная декартова, цилиндрическая и сферическая системы координат. Будем пользоваться в основном прямоугольной декартовой системой координат (рис.), в которой положение материальной точки М определяется тремя координатами х, у и z. При движении точки эти координаты изменяются во времени и, следовательно, ее движение описывается тремя уравнениями. Естественный(траекторный) Если точка М движется по некоторой заданной траектории, то для описания движения достаточно выбрать на траектории начало отсчета, положительное и отрицательное направления отсчета длины дуги которую называют дуговой координатой. Зависимость S(t) задает движение точки в естественном способе описания движения.
Тангенциал., нормал. и полное ускорение
Угловые кинематические величины
Связь между лин скоростью и угловой: Если ω=const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2π. Так как промежутку времени ∆t = Т соответствует ∆φ= 2π, то ω = 2π/ T, откуда T =2π /ω Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения: ν=1/T=ω/(2π), откуда
ω=2πν.
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору со (см рис.), при замедленном — противонаправлен ему. Таким образом, связь между линейными и угловыми величинами выражается следующими формулами: s=Rφ, v=Rω, аt=Rε, аn= ω2R В случае равнопеременного движения точки по окружности (ε=const) ω=ω0± εt, φ=ω0± εt2/2 где ω0 – начальная угловая скорость.
Законы Ньютона
Деформации. Силы упругости. Закон Гука Деформация – изменение размера или формы. При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости. При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации: Fx = Fупр = –kx. закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ: Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах.
Момент инерции. Теорема Штейнера.
Главные оси
Плоское движение Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:
Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений(теорема Кёнига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения. Физический маятник Физический маятник ‑ это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку A, не совпадающую с центром масс С тела. Если маятник отклонен на угол α, то момент возвращающей силы можно записать в виде (22) где J ‑ момент инерции маятника, относительно оси, проходящей через точку подвеса A, l ‑ расстояние от точки A до центра масс маятника, возвращающая сила. Волновое уравнение
,где -оператор Лапласа
и
Формула Пуазейля.
Приборы, служащие для определения вязкости по этому методу, называются вискозиметрами. 30-31 Сложение гармонических колебаний одинаковой частоты. x1=A1cos(wt+j1), x2=A2cos(wt+j2). Представим в комплексной форме: x=x1+x2=A1ei(wt+j1)+ A2ei(wt+j2)=eiwt(A1eij1+A2eij2), A1eij1+A2eij2=Aeij, A2=A12+A22+2 A1A2cos(j1–j2,), tg j=(A1sinj1+A2sinj2)/(A1cosj1+A2cosj2) Þ x=x1+x2=Aei(wt+j) Þ x=Acos(w t–j). Сложения гармонических колебаний с близкими частотами. x1=A1cos(w1t+j1), x2=A2cos(w2t+j2). Каждое из колебаний представим в комплексной форме, а сложение будем производить векторно. Пусть A1>A2. Cуммой двух колебаний с близкими частотами является колебание с изменяющейся амплитудой (от А1–А2 до А1+А2) и с частотой |w1–w2|. Колебания амплитуды с частотой W=|w1–w2| называются с биениями, а частота W – частотой биения. Космические скорости
Условие неразрывности струи утверждает, что при ламинарном течении жидкости произведение площади сечения участка, через который она протекает, на ее скорость является постоянной величиной для данной трубки тока.Sv = const. При описании физических законов течения крови по сосудам вводится допущение, что количество циркулирующей крови в организме постоянно. Отсюда следует формулировка условия неразрывности струи для реальной гемодинамики:В любом сечении сердечно-сосудистой системы объемная скорость. кровотока постоянна:Q = const.Под площадью сечения сосудистой системы понимают суммарную площадь сечения кровеносных сосудов одного уровня ветвления. Например, в большом круге кровообращения первое (наименьшее по площади) сечение проходит через аорту, второе - через все артерии, на которые непосредственно разветвляется аорта, и т.д. Наибольшую площадь имеет сечение, соответствующее капиллярной сети.Из условия неразрывности струи следует,что с увеличением площади сечения сосудистой системы скорость кровотока в ее соответствующих участках уменьшается.
36. Скорость распостранения волн
Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле: где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.
33. Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так: , или Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:
Способы описания движения М.Т. Векторный При таком способе описания движения на теле отсчета выбирается точка О (начало отсчета), из которой в направлении движущейся точки М проводят радиус-вектор (рис.). При движении точки М значение и направление радиуса-вектора r изменяются, т. е. он является функцией времени. Если вид функции r = r (t) известен, то уравнение движения точки М задано в векторной форме. Конец радиуса-вектора r (t) описывает в пространстве кривую, которая называется траекторией движущейся точки. Координатный В этом случае с телом отсчета связывается система координат, которая позволяет каждой точке пространства сопоставить три числа, называемые координатами точки этого пространства. Наиболее распространенными системами являются прямоугольная декартова, цилиндрическая и сферическая системы координат. Будем пользоваться в основном прямоугольной декартовой системой координат (рис.), в которой положение материальной точки М определяется тремя координатами х, у и z. При движении точки эти координаты изменяются во времени и, следовательно, ее движение описывается тремя уравнениями. Естественный(траекторный) Если точка М движется по некоторой заданной траектории, то для описания движения достаточно выбрать на траектории начало отсчета, положительное и отрицательное направления отсчета длины дуги которую называют дуговой координатой. Зависимость S(t) задает движение точки в естественном способе описания движения.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.85.189 (0.011 с.) |



 Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: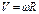 Единица измерения угловой скорости — радиан в секунду (рад/с).
Единица измерения угловой скорости — радиан в секунду (рад/с).
 Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:



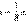 Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.



 где v0 – скорость центра масс тела, ui – скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:
где v0 – скорость центра масс тела, ui – скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим: Так как
Так как  (суммарный импульс частиц в системе центра масс равен нулю).
(суммарный импульс частиц в системе центра масс равен нулю).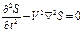 Волновое уравнение
Волновое уравнение
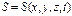
 Формула Пуазейля используется при определении коэффициента η для вязких сред путем измерения объема V вытекшей жидкости за некоторое время t при заданном перепаде давлений Δ р=р1 —р2
Формула Пуазейля используется при определении коэффициента η для вязких сред путем измерения объема V вытекшей жидкости за некоторое время t при заданном перепаде давлений Δ р=р1 —р2

 , а поперечной:
, а поперечной: 
 , т.е.
, т.е.
 . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой.
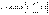 .
.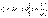 .
.


