
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос2. Криволинейное движениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопрос2. Криволинейное движение Тангенциальная составляющая ускорения
т. е., определяет быстроту изменения скорости по модулю. Вторая составляющая ускорения, равная называется нормальной составляющей ускорения и направлена по нормали к траектории к центру се кривизны (поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 1.5): тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения – быстроту изменения скорости по направлению (направлена к центру кривизны траектории). Равнопеременное движение
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом: 1) 2) 3) 4) 5) 6) 7) Вопрос3 Кинематика вращательного движения Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: Тангенциальная составляющая ускорения Нормальная составляющая ускорения
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение В случае равнопеременного движения точки по окружности (
Вопрос 4 Законы динамики Ньютона Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Свойство тела сохранять свое состояние называется инертностью. Поэтому первый закон Ньютона называют законом инерции. Инерционная система отсчёта – система отсчёта, относительно которой тело при отсутствии внешних воздействий движется прямолинейно и равномерно. Масса тела – физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. Сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. Основной закон динамики поступательного движения – это второй закон Ньютона, он определяет, как изменяется механическое движение материальной точки или тела под действием приложенных сил. Второй закон Ньютона: ускорение, приобретаемое материальной точкой или телом, пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:
Вопрос 6 Работа, мощность. . Элементарной работой силы F на перемещении dr называется скалярная величина dA = F d r = F cos ds = Fsds, где – угол между векторами F и d r; ds =| d r | – элементарный путь; F s – проекция вектора F на вектор d r
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути, а в пределе интегралу
Единица работы – джоуль (Дж): 1 Дж – работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Нм). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности
За время dt сила F совершает работу F d r, и мощность, развиваемая этой силой, в данный момент времени т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N – величина скалярная. Единица мощности – ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт=1 Дж/с).
Вопрос 7 Энергия Кинетическая энергия механической системы – это энергия ее механического движения этой системы. Таким образом, тело массой т, движущееся со скоростью v, обладает кинетической энергией
потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Если работа, совершаемая под действием силовых полей при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений, то поля называются потенциальными, а силы, действующие в них, – консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; например сила трения. Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при бесконечно малом изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
Вопрос 16 Идеальный газ Для вывода основного уравнения молекулярно-кинетической теории рассмотрим идеальный одноатомный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку S (рисунок 2.5) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс
где m0 – масса молекулы, v – ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой v t (рисунок 2.5). Число этих молекул равно n Sv t (n – концентрация молекул). Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул. Половина этих молекул (т.е. 1/6 часть) движется вдоль данного направления в одну сторону, а вторая половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет 1/6 n Sv t. При столкновении с площадкой эти молекулы передадут ей импульс
Тогда давление газа, оказываемое им на стенку сосуда,
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2,..., vN, то целесообразно рассматривать среднюю квадратичную скорость
характеризующую всю совокупность молекул газа. Уравнение (2.23) с учетом (2.24) примет вид
Выражение (2.25) называется основным уравнением молекулярно-кинетической теории идеальных газов.
Уравнению удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона – Менделеева. В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;2) между молекулами газа отсутствуют силы взаимодействия;3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно использовать при изучении реальных газов в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах.
Вопрос 20 Теплоемкость Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Единица удельной теплоемкости – джоуль на килограмм-кельвин (Дж/(кг×К)). Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К:
где v=m/M – количество вещества. Единица молярной теплоемкости – джоуль на моль-кельвин (Дж/(моль×К)). Удельная теплоемкость с связана с молярной Сm соотношением
где М – молярная масса вещества. Если в процессе нагревания вещества его объем или давление поддерживается постоянными, то получают теплоемкости при постоянном объеме и постоянном давлении. Запишем выражение первого начала термодинамики (2.79) для 1 моль газа с учетом значений dQ и dА:
Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (см. (2.80)) и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:
т. е. молярная теплоемкость газа при постоянном объеме СV равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1 К. Подставим
Если газ нагревается при постоянном давлении, то выражение (2.85) можно записать в виде
Учитывая, что
Выражение (2.89) называется уравнением Майера; оно показывает, что CP, всегда больше СV на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа. Использовав (2.87), выражение (2.89) можно записать в вид
Характеристикой для каждого газа является отношение СP к СV:
Молярные теплоемкости одноатомных газов определяются числом степеней свободы и не зависят от температуры в широком интервале температур. У двухатомных газов число степеней свободы зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными и одной колебательной степенями свободы. Из экспериментальной зависимости молярной теплоемкости СV водорода (рисунок 2.21) следует, что при низкой температуре (»50 К) СV=3/2R, при комнатной – СV=5/2R и при очень высокой – СV=7/2R. Следовательно, при низких температурах наблюдается только поступательное движение молекул, при комнатных – добавляетсяих вращение, а при высоких – к этим двум видам движения добавляются еще колебания молекул.
Рисунок 2.21 При вычислении теплоемкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определенный дискретный ряд значений энергий). Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания «замораживается» и не вносят своего вклада в теплоемкос
Закон Кулона Точечным называется заряд, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует. Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними:
где k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной. В случае разноименных зарядов возникает притяжение (F<0), в случае одноименных зарядов - отталкивание (F>0). Эта сила называется кулоновской силой. В векторной форме закон Кулона имеет вид:
где F В СИ коэффициент пропорциональности равен k=
Величина
Формула (3.7) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
Вопрос 28 Потенциал Работа консервативны сил совершается за счет убыли потенциальной энергии. Работу сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q в начальной и конечной точках поля заряда Q:
Отношение U/Q Потенциал Потенциал поля, создаваемого точечным зарядом Q, равен Работа, совершаемая силами электростатического поля при перемещении заряда Q
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля при перемещении положительного единичного заряда из точки 1 в точку 2.
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения. Если перемещать заряд Q A откуда
Таким образом, потенциал — физическая величина, определяемая работой по перемещению положительного единичного заряда при удалении его из данной точки поля в бесконечность. Единица потенциала — вольт (В): 1 В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В= 1 Дж/Кл). Если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов. Элементарная работа сил электростатического поля переноса положительного единичного точечного заряда на пути dl равна E d l = E Интеграл Формула справедлива только для электростатического поля.
Вопрос 62 Эффект Комптона Наиболее полно корпускулярные свойства света проявляются в эффекте Комптона. Американский физик А. Комптон (1892—1962), исследуя в 1923 г. рассеяние монохроматического рентгеновского излучения веществами с легкими атомами (парафин, бор), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также более длинноволновое излучение. Опыты показали, что разность Δλ=λ'-λ=2λcsin2(θ/2), Где Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и Объяснение эффекта Комптона дано на основе квантовых представлений о природе света. Если считать, как это делает квантовая теория, что излучение имеет корпускулярную природу, т. e. представляет собой поток фотонов, то эффект Комптона — результат упругого столкновения рентгеновских фотонов со свободными электронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон передаст электрону часть своих энергии и импульса в соответствии с законами их сохранения. Рассмотрим упругое столкновение двух частиц (рис.6.13) — налетающего фотона, обладающего импульсом Согласно закону сохранения энергии, а согласно закону сохранения импульса, где
Решая уравнения (6.21) и (6.22) совместно, получим Поскольку Выражение (6.23) есть не что иное, как полученная экспериментально Комптоном формула (6.18). Подстановка в нее значений Наличие в составе рассеянного излучения несмещенной линии (излучения первоначальной длины волны) можно объяснить следующим образом. При рассмотрении механизма рассеяния предполагалось, что фотон соударяется лишь со свободным электроном. Однако если электрон сильно связан с атомом, как это имеет место для внутренних электронов (особенно в тяжелых атомах), то фотон обменивается энергией и импульсом с атомом в целом. Tax как масса атома по сравнению с массой электрона очень велика, то атому передастся лишь ничтожная часть энергии фотона. Поэтому в данном случае длина волны Из приведенных рассуждений следует также, что эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон нельзя считать свободным. Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например протонах, однако из-за большой массы протона его отдача «просматривается» лишь при рассеянии фотонов очень высоких энергий. Как эффект Комптона, так и фотоэффект на основе квантовых представлений обусловлены взаимодействием фотонов с электронами. В первом случае фотон рассеивается, во втором — поглощается. Рассеяние происходит при взаимодействии фотона со свободным электроном, а фотоэффект - со связанными электронами. Можно показать, что при столкновении фотона со свободным электроном не может произойти поглощения фотона, так как это находится в противоречии с законами сохранения импульса и энергии. Поэтому при взаимодействии фотонов со свободными электронами может наблюдаться только их рассеяние, т. е. эффект Комптона. Вопрос 66 Волновая функция. Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противоречие целого ряда экспериментов с применяемыми в начале XX в. теориями, привели к новому этапу развития квантовой теории - созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств.Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX в.; оно связано прежде всего с работами австрийского физика Э. Шредингера (1887—1961), немецкого физика В. Гсйзенберга и английского физика П. Дирака (1902—1984). На данном этапе развития возникли новые принципиальные проблемы, в частности проблема физической природы волн де Бройля. Для выяснения этой проблемы сравним дифракцию световых волн и микрочастиц. Дифракционная картина, наблюдаемая для световых волн, характеризуется тем, что в результате наложения дифрагирующих волн друг на друга в различных точках пространства происходит усиление или ослабление амплитуды колебаний. Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. По представлениям фотонной теории, интенсивность определяется числом фотонов, попадающий в данную точку дифракционной картины. Следовательно, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды определяет вероятность попадания фотона в ту или иную точку. Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков микрочастиц, рассеянных или отраженных по различным направлениям, - в одних направлениях наблюдается большее число частиц, чем в других. Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. С другой стороны, интенсивность волн де Бройля оказывается больше там, где имеется большее число частиц, т.е. интенсивность волн де Бройля в данной точке пространства определяет число частиц, попавших в эту точку. Таким образом, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая. Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Можно ли волны де Бройля истолковывать как волны вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла. Чтобы устранить эти трудности, немецкий физик М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая ( Итак, в квантовой механике состояние ми
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 541; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.104.36 (0.011 с.) |







 ,
,  – прямолинейное равномерное движение;
– прямолинейное равномерное движение;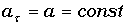 ,
, 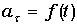 ,
,  . При
. При  – равномерное криволинейное движение;
– равномерное криволинейное движение; ,
, 
 Вектор
Вектор  так же, как и вектор
так же, как и вектор  . Размерность угловой скорости
. Размерность угловой скорости 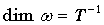 , а ее единица – радиан в секунду (рад/с).
, а ее единица – радиан в секунду (рад/с).
 и
и  .
. .
. нормальное ускорение
нормальное ускорение  ) и угловыми величинами (угол поворота
) и угловыми величинами (угол поворота  , угловая скорость
, угловая скорость  , угловое ускорение
, угловое ускорение  ) выражается следующими формулами:
) выражается следующими формулами:  ,
,  ,
,  ,
, 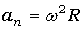 .
. ,
,  где
где 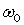 – начальная угловая скорость.
– начальная угловая скорость.



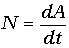

 А=Fs=ma(V22-V21)/2a=(mV22/2)-(mV21/2)
Т=mV2/2
A=T2-T1
А=Fs=ma(V22-V21)/2a=(mV22/2)-(mV21/2)
Т=mV2/2
A=T2-T1
 ,
,




 , тогда
, тогда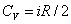

 не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна СV (см. (2.86)), и дифференцируя уравнение Клапейрона – Менделеева pVm=RT (2.16) пo T (p = const), получаем
не зависит от вида процесса (внутренняя энергия идеального газа не зависит ни от p, ни от V, а определяется лишь температурой Т) и всегда равна СV (см. (2.86)), и дифференцируя уравнение Клапейрона – Менделеева pVm=RT (2.16) пo T (p = const), получаем
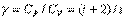


 F
F  =
= 
 со стороны заряда Q
со стороны заряда Q  , r
, r 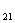 = - F
= - F  Тогда закон Кулона запишется в окончательном виде:
Тогда закон Кулона запишется в окончательном виде: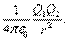
 относится к числу фундаментальных физических постоянных и называется электрической постоянной:
относится к числу фундаментальных физических постоянных и называется электрической постоянной:  =9109 м/Ф.
=9109 м/Ф.
 = U
= U  не зависит от Q
не зависит от Q 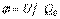
 в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией положительного единичного заряда, помещенного в эту точку.
в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией положительного единичного заряда, помещенного в эту точку.
 ), не зависит от траектории перемещения
), не зависит от траектории перемещения
 =
= 
 = Q
= Q  dl, где E
dl, где E  — проекция вектора Е на направление элементарного перемещения.
— проекция вектора Е на направление элементарного перемещения.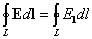 называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю, следовательно, линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и заканчиваются на зарядах или же уходят в бесконечность.
называется циркуляцией вектора напряженности. Циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю, следовательно, линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и заканчиваются на зарядах или же уходят в бесконечность.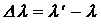 не зависит от длины волны
не зависит от длины волны 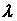 падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния
падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния 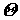 θ:
θ: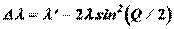 (6.18)
(6.18)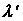 - длина волны рассеянного излучения,
- длина волны рассеянного излучения, 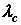 комптоновская длина волны (при рассеянии фотона на электроне
комптоновская длина волны (при рассеянии фотона на электроне 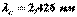 ).
).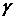 - излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.
- излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.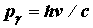 и энергией
и энергией 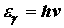 , с покоящимся свободным электроном (энергия покоя
, с покоящимся свободным электроном (энергия покоя 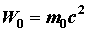 ;
; 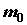 - масса покоя электрона). Фотон, столкнувшись с электроном, передаетему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы сохранения энергии и импульса.
- масса покоя электрона). Фотон, столкнувшись с электроном, передаетему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы сохранения энергии и импульса.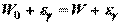 (6.19)
(6.19)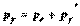 (6.20)
(6.20)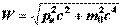 - энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значительна),
- энергия электрона после столкновения (используется релятивистская формула, так как скорость электрона отдачи в общем случае значительна), 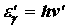 - энергия рассеянного фотона. Подставив в выражение (6.19) значения величин и представив (6.20) в соответствии с рис.6.13, получим
- энергия рассеянного фотона. Подставив в выражение (6.19) значения величин и представив (6.20) в соответствии с рис.6.13, получим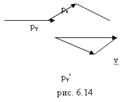
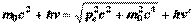 (6.21)
(6.21)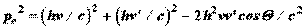 (6.22)
(6.22)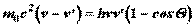
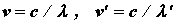 и
и 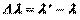 , получим
, получим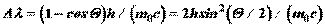 (6.23)
(6.23)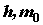 и
и 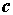 даст комптоновскую длину волны электрона
даст комптоновскую длину волны электрона 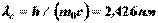 .
.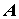 падающего излучения.
падающего излучения. Эту величину называют. также волновой функцией (или
Эту величину называют. также волновой функцией (или  - функцией). Амплитуда вероятности может быть комплексной, и вероятность
- функцией). Амплитуда вероятности может быть комплексной, и вероятность  пропорциональна квадрату ее модуля:
пропорциональна квадрату ее модуля: (6.46)
(6.46) ,
,  - функция, комплексно сопряженная с
- функция, комплексно сопряженная с 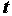 ,в области с координатами
,в области с координатами  и
и  ,
,  и
и 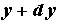 ,
,  и
и 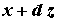 .
.


