Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторный способ описания движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В этом случае положение частицы задается её радиус-вектором Зависимость радиус-вектора частицы от времени Изменение радиус-вектора Скоростью частицы называется векторная величина, определяемая равенством Из определения следует, что скорость
Таким образом, зная кинематический закон движения, можно простым дифференцированием по времени найти скорость и ускорение в любой Наоборот, зная ускорение частицы, а также начальные условия, т.е. положение
Координатный способ описания движения Если с телом отсчета жестко связать какую-нибудь координатную систему (например, декартову), то положение частицы в любой момент времени определяется тремя ее координатами x,y,z.Проектируя радиус-вектор на координатные оси, получим три зависимости координат частицы от времени Модули скорости и ускорения будут
Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
Рис. 1.19. Траектория и вектор перемещения при криволинейном движении. При движении по криволинейной траектории вектор перемещения
Рис. 1.20. Мгновенная скорость при криволинейном движении. Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:
или
Где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0 соответственно. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему. Нормальное ускорение - это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости. Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности. Полное ускорение при равнопеременном криволинейном движении тела равно:
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).
Движение точки по окружности может быть очень сложным (рис. 17). Рассмотрим подробно движение точки по окружности, при котором v = const. Такое движение называется равномерным движением по окружности. Естественно, вектор скорости не может быть неизменным (v не равно const), так как направление скорости постоянно меняется. Время, за которое траектория точки опишет окружность, называется периодом обращения точки (Т). Число оборотов точки в одну секунду называется частотой обращения (v). Период обращения можно найти по формуле:
Естественно, перемещение точки за один оборот будет равно нулю. Однако пройденный путь будет равен 2ПиR, а при числе оборотов п путь будет равен 2ПиRn или 2ПиRt/T, где t - время движения. Ускорение при равномерном движении точки по окружности направлено к ее центру и численно равно а = v2/R. Это ускорение называется центростремительным (или нормальным). Вывод этого равенства может быть следующим. Приведем векторы скорости к одной точке хотя бы за - Т (можно и за Т/2 или Т) (рис. 18).
Тогда сумма изменений векторов скоростей за малые промежутки времени будет равна длине дуги АВ, которая равна модулю | v2 - v1 | за время t = 1/4*Т. Определим длину дуги. Поскольку радиусом для дуги будет модуль вектора v1=v2=v, то длина дуги l может быть вычислена как длина четверти окружности с радиусом v:
После сокращения получим:
Если же движение равнопеременное, то v Ф const, тогда рассматривают другую составляющую ускорения, обеспечивающую изменение модуля скорости. Это ускорение называется тангенциальным:
Тангенциальное ускорение направлено по касательной к траектории, оно может совпадать по направлению со скоростью (движение равноускоренное) или быть противоположно направленным (движение равнозамедленное).
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.209.178 (0.007 с.) |

 . Геометрическое место концов радиус-вектора представляет кривую,
. Геометрическое место концов радиус-вектора представляет кривую, называется кинематическим уравнением движения. С геометрической
называется кинематическим уравнением движения. С геометрической . Длина дуги траектории между этими точками ∆l назывется путем.
. Длина дуги траектории между этими точками ∆l назывется путем.  ,
, направлена по касательной к траектории. Величина скорости
направлена по касательной к траектории. Величина скорости  ,
,

 и скорость
и скорость  частицы в начальный момент времени,
частицы в начальный момент времени, (обратная задача кинематики).
(обратная задача кинематики).
 и
и 
 и
и 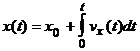
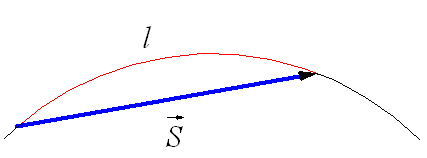
 направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).