
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неинерциональные системы отсчета .Силы инерции. Центробежная сила инерции .Кориолисова сила инерции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью. Для согласования сил и ускорений в неинерциальной системе отсчёта, перечень действующих на тела сил можно дополнить силами инерции. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. СИЛА ИНЕРЦИИ - векторная величина, численно равная произведению массы т материальной точки на её ускорение w и направленная противоположно ускорению. При криволинейном движении С. и. можно разложить на касательную, или тангенциальную, составляющую Центробе́жная си́ла [1] — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил. Сила Кориолиса (по имени французского ученого Г. Г. Кориолиса) – одна из сил инерции, существующая в системе отсчета, вращающейся и проявляется при движении в направлении под углом к оси вращения. Причина появления силы Кориолиса в кориолисовым ускорении. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где а – кориолисово ускорения. Соответственно, тело действует согласно третьему закону Ньютона с силой противоположной направленности. F K =-ma. Сила, действующая со стороны тела, и будет называться силой Кориолиса. При вращении диска, далеки от центра точки движутся с тем большей касательной скоростью, чем менее далекие. Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе, то нам придется увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчета вращается вместе с диском, то мы почувствуем, что тело «не хочет» оставаться на радиусе, а «норовит» сместиться – это и есть сила Кориолиса.
В инерциальных системах отсчета действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что для того чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем больше должна быть касательная скорость вращения. Это означает, что с точки зрения системы отсчета, вращающейся некая сила будет пытаться сместить тело с радиуса. Если вращение происходит по часовой стрелке, то тело, движется от центра вращения, стремится сойти с радиуса влево. Если вращение происходит против часовой стрелки – то вправо. В системе координат, которая вращается вокруг оси с угловой скоростью, Тело, движущееся с линейной скоростью, Имеет ускорение
. Соответствующая сила, которая заставляет тело двигаться с таким ускорением должна равняться
где m – масса тела. Кориолисова сила перпендикулярна оси вращения и к скорости тела. Если тело движется вдоль оси вращения, кориолисовым силы не возникает. Наибольшее значение Кориолисова сила тогда, когда тело движется перпендикулярно оси вращен
14. Закон всемирного тяготения. Энергия гравитационного взаимодействия. закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними:
Векторы сил всемирного тяготения направлены вдоль прямой, соединяющей тела. Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением
15.
|
|||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 750; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.224 (0.01 с.) |

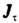 , направленную противоположно касат. ускорению, и на нормальную, или центробежную, составляющую, направленную вдоль гл. нормали траектории от центра кривизны; численно
, направленную противоположно касат. ускорению, и на нормальную, или центробежную, составляющую, направленную вдоль гл. нормали траектории от центра кривизны; численно  ,,
,,  где v - скорость точки,
где v - скорость точки,  - радиус кривизны траектории. При изучении движения по отношению к инерциальной системе отсчёта С. и. вводят для того, чтобы иметь формальную возможность составлять ур-ния динамики в форме более простых ур-ний статики
- радиус кривизны траектории. При изучении движения по отношению к инерциальной системе отсчёта С. и. вводят для того, чтобы иметь формальную возможность составлять ур-ния динамики в форме более простых ур-ний статики






