
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система отсчета. Траектория, длина пути, вектор перемещения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Система отсчета. Траектория, длина пути, вектор перемещения.
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом отсчета. При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями
эквивалентными векторному уравнению r = r(t). (1.2) Уравнения (1.1) (соответственно (1.2)) называются кинематическими уравнениями движения материальной точки.
Cкорость. Средняя и мгновенная скорости. Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени. Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0 (рис. 3). В течение малого промежутка времени Dt точка пройдет путь As и получит элементарное (бесконечно малое) перемещение Dr. Вектором средней скорости <v > называется отношение приращения Dr радиуса-вектора точки к промежутку времени Dt:
Направление вектора средней скорости совпадает с направлением Dr. При неограниченном уменьшении Dt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:
По мере уменьшения Dt путь Ds все больше будет приближаться к |Dr|, поэтому модуль мгновенной скорости Таким образом, модуль мгновенной скорости равен первой производной пути по времени:
При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной (v) — средней скоростью неравномерного движения:
В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид
Длина пути, пройденного точкой за промежуток времени от t 1до t 2, дается интегралом
Работа силы. Мощность. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол а с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = Fcosa), умноженной на перемещение точки приложения силы: A = Fss = Fs cosa. (11.1) В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным. Элементарной работой силы F на перемещении d r называется скалярная величина dА = F d r = F cosa• ds=Fsds, где а — угол между векторами F и d r; ds = |d r | — элементарный путь; Fs — проекция вектора F на вектор d r (рис. 13). Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
Для вычисления этого интеграла надо знать зависимость силы Fs от пути s вдоль траектории 1 — 2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графике площадью закрашенной фигуры. Если, например, тело движется прямолинейно, сила F=const и a=const, то получим
где s — пройденный телом путь (см. также формулу (11.1)). Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой в 1 Н на пути в 1 м (1 Дж = 1 Н•м). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности: N=da/dt. (11.3) За время dt сила F совершает работу F d r, и мощность, развиваемая этой силой, в данный момент времени N= F d r /dt= Fv т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная. Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа в 1 Дж (1 Вт = 1 Дж/с).
10. Преобразования Галилея. Механический принцип относительности. Преобразова́ния Галиле́я — в классической механике преобразования координат и времени при переходе от одной инерциальной системы отсчета к другой. Пусть система к – инерциальная система отсчета и к’. к’ движется равномерно и прямолинейно со скоростью u. Тогда
x=x’+
a= Таким образом система отсчета к’, движущийся равномерно и прямолинейно относительно инерциальной системы отсчета к, также будет инерциальной. Во всех инерциальных системах отсчета равенство ускорений а и а’ означает, что законы классической динамики имеют одинаковую формулу.
Система отсчета. Траектория, длина пути, вектор перемещения.
Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Понятие материальной точки — абстрактное, но его введение облегчает решение практических задач. Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводится к изучению системы материальных точек. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками (или точнее между двумя частицами) этого тела остается постоянным. Поступательное движение — это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета — совокупность системы координат и часов, связанных с телом отсчета. При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями
эквивалентными векторному уравнению r = r(t). (1.2) Уравнения (1.1) (соответственно (1.2)) называются кинематическими уравнениями движения материальной точки.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.132.107 (0.009 с.) |


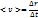


 (2.2)
(2.2)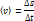
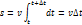

 (11.2)
(11.2)

 t
t t
t y=y’++
y=y’++  z=z’++
z=z’++  t=t’
t=t’ =
=  =
= 
 =
=  ’ a=a’; если а=0, то и а’=0
’ a=a’; если а=0, то и а’=0


