
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силы инерции во вращающейся системе отсчета и их применение. Сила кориолиса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При движении тела относительно вращающейся системы отсчета, кроме центростремительной и центробежной сил, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции
Здесь Сила Кориолиса вызывает кориолисово ускорение. Выражение для этого ускорения имеет вид
Ускорение направлено перпендикулярно векторам Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу. Таким образом, Влияние кориолисовых сил необходимо учитывать в ряде случаев при истолковании явлений, связанных с движением тел относительно земной поверхности. Если тело удаляется от оси вращения, то сила С учетом всех сил инерции, уравнение Ньютона для неинерциальной системы отсчета примет вид:
17. Преобразование координат Галилея. Механический принцип относительности. Закон сложения скоростей. Инварианты преобразования.
Дифференцируя эти уравнения по времени и учитывая, что
Таким образом, если в системе К тело имеет ускорение а, то такое же ускорение оно имеет и в системе К’. Согласно второму закону Ньютона:
т.е. второй закон Ньютона одинаков в обоих случаях. При Механический принцип относительности 1. Координаты и время в двух произвольных инерциальных системах отсчета связаны преобразованием Галилея: где r и r' - раднус-векторы движущейся точки в первой и второй системах отсчета, ve - скорость равномерного и прямолинейного движения второй системы по отношению к первой, а r0 - радиус-вектор, проведенный из начала первой системы в начало второй системы в момент времени t = 0. Второе условие (t' = t) выражает абсолютный характер времени в классической механике, т. е. одинаковость его течения во всех инерциальных системах отсчета. a' = dv'/dt = dv/dt = a Ускорение какой-либо материальной точки во всех инерциальных системах одинаково. Поэтому одинаковы и силы, действующие на движущуюся материальную точку: Следовательно т.е. уравнения движении материальной точки и систем этих точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованию Галилея. Закон сложения скоростей Рассмотрим две инерциальные системы отсчета k и k '. Система k ' движется относительно k со скоростью v = const вдоль оси x. Точка М движется в двух системах отсчета (рис. 8.1).
Найдем связь между координатами точки M в обеих системах отсчета. Отсчет начнем, когда начала координат систем совпадают, то есть t = t '. Тогда:
Совокупность уравнений (8.1.1) называется преобразованиями Галилея. В уравнениях (8.1.1) время t = t ', т.е. в классической механике предполагалось, что время течет одинаково в обеих системах отсчета независимо от скорости. («Существует абсолютное время, которое течет всегда одинаково и равномерно», – говорил Ньютон). В векторной форме преобразования Галилея можно записать так:
Продифференцируем это выражение по времени, получим (рис. 8.2):
Выражение (8.1.3) определяет закон сложения скоростей в классической механике. Из него следует, что скорость движения точки М (сигнала) Инвариа́нт в физике — физическая величина, значение которой в некотором физическом процессе не изменяется с течением времени.[1] Примеры: энергия, компоненты импульса и момента импульса в замкнутых системах. Также инвариантами называются величины, независимые от условий наблюдения, в особенности — от системы отсчета — например интервал в теории относительности инвариантен в этом смысле. Промежуток времени между двумя событиями, а также расстояние между ними (местами событий) для наблюдателей, движущихся в различных направлениях с разными скоростями, будут разными, однако интервал между этими событиями для всех наблюдателей будет один. К этой же категории относится, например скорость света в вакууме. Такие величины, в зависимости от класса систем отсчета, при переходе между которыми сохраняется инвариантность данной величины, называют лоренц-инвариантными (инвариантами группы Лоренца) или инвариантами группы общекоординатных преобразований (рассматриваемыми в общей теории относительности); для ньютоновской физики может иметь смысл также рассматривать инвариантность относительно преобразований Галилея (инвариантными относительно таких преобразований являются компоненты ускорения и силы). Понятие инвариантности (инвариантов) в физике лежит в русле принятого в математике понятия «инвариант преобразований (группы преобразований)» (той или иной конкретной группы преобразований — сдвигов времени, преобразований Лоренца и т. п.). 18. Постулаты специальной теории относительности. Преобразования Лоренца. Относительность одновременности. Постулаты СТО. Классическая механика Ньютона прекрасно описывает движение макротел, движущихся с малыми скоростями (υ << c). В нерелятивистской физике принималось как очевидный факт существование единого мирового времени t, одинакового во всех системах отсчета. В основе классической механики лежит механический принцип относительности (или принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета. Этот принцип означает, что законы динамики инвариантны (т. е. неизменны) относительно преобразований Галилея, которые позволяют вычислить координаты движущегося тела в одной инерциальной системе (K), если заданы координаты этого тела в другой инерциальной системе (K'). Итак, на рубеже XIX и XX веков физика переживала глубокий кризис. Выход был найден Эйнштейном ценой отказа от классических представлений о пространстве и времени. Наиболее важным шагом на этом пути явился пересмотр используемого в классической физике понятия абсолютного времени. Классические представления, кажущиеся наглядными и очевидными, в действительности оказались несостоятельными. Многие понятия и величины, которые в нерелятивистской физике считались абсолютными, т. е. не зависящими от системы отсчета, в эйнштейновской теории относительности переведены в разряд относительных. Так как все физические явления происходят в пространстве и во времени, новая концепция пространственно-временных закономерностей не могла не затронуть в итоге всю физику. В основе специальной теории относительности лежат два принципа или постулата, сформулированные Эйнштейном в 1905 г. Принцип относительности: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму. Таким образом, принцип относительности классической механики обобщается на все процессы природы, в том числе и на электромагнитные. Этот обобщенный принцип называют принципом относительности Эйнштейна. Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую. Эти принципы следует рассматривать как обобщение всей совокупности опытных фактов. Следствия из теории, созданной на основе этих принципов, подтверждались бесконечными опытными проверками. СТО позволила разрешить все проблемы «доэйнштейновской» физики и объяснить «противоречивые» результаты известных к тому времени экспериментов в области электродинамики и оптики. В последующее время СТО была подкреплена экспериментальными данными, полученными при изучении движения быстрых частиц в ускорителях, атомных процессов, ядерных реакций и т. п.
Преобразования Лоренца. Классические преобразования Галилея несовместимы с постулатами СТО и, следовательно, должны быть заменены. Эти новые преобразования должны установить связь между координатами (x, y, z) и моментом времени t события, наблюдаемого в системе отсчета K, и координатами (x', y', z') и моментом времени t' этого же события, наблюдаемого в системе отсчета K'. Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:
Относительность одновременности. Два любых события в точках А и В, одновременные в системе К1 не одновременны в системе К. Но в силу принципа относительности системы К1 и К совершенно равноправны. Ни одной из этих систем нельзя отдать предпочтение. Поэтому мы вынуждены прийти к заключению, что одновременность пространственно разделенных событий относительна. Причиной относительности одновременности является, как мы видим, конечность скорости распространения сигналов.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.015 с.) |


 – сила Кориолиса, также являющаяся силой инерции,
– сила Кориолиса, также являющаяся силой инерции,  – угловая скорость вращения диска.
– угловая скорость вращения диска.
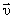 и
и 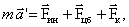
 – сила инерции, обусловленная поступательным движением неинерциальной системы отсчета;
– сила инерции, обусловленная поступательным движением неинерциальной системы отсчета; 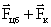 – две силы инерции, обусловленные вращательным движением системы отсчета;
– две силы инерции, обусловленные вращательным движением системы отсчета;  – ускорение тела относительно неинерциальной системы отсчета:
– ускорение тела относительно неинерциальной системы отсчета: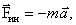

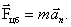

 (K’). Координаты тела М в системе К x:y:z, а в системе К’ - x’:y’:z’. Эти координаты связаны между собой соотношениями, которые называються преообразованием Галилея
(K’). Координаты тела М в системе К x:y:z, а в системе К’ - x’:y’:z’. Эти координаты связаны между собой соотношениями, которые называються преообразованием Галилея
 , найдем соотношения между скоростями и ускорениями:
, найдем соотношения между скоростями и ускорениями: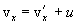

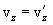


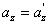

 движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея. Этот результат называется механическим принципом относительности (принцип относительности Галилея), и формулируется следующим образом: равномерное и прямолинейное движение (относительно какой-либо инерциальной системы отсчета) замкнутой системы не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Поэтому никакими механическими опытами внутри системы нельзя обнаружить движется ли система равномерно и прямолинейно или покоится.
движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки, а также для произвольной системы материальных точек одинаковы во всех инерциальных системах отсчета - инвариантны по отношению к преобразованиям Галилея. Этот результат называется механическим принципом относительности (принцип относительности Галилея), и формулируется следующим образом: равномерное и прямолинейное движение (относительно какой-либо инерциальной системы отсчета) замкнутой системы не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Поэтому никакими механическими опытами внутри системы нельзя обнаружить движется ли система равномерно и прямолинейно или покоится.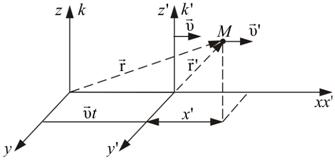


 или
или 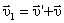 .
.

 в системе k ' и
в системе k ' и  в системе k различна.
в системе k различна. β = υ / c.
β = υ / c.



