Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отступление от законов идеальных газов. Реальные газы. Силы и потенциальная энергия межмолекулярного взаимодействия. Эффективный диаметр молекул.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Отступление от законов идеальных газов. Законы идеальных газов - приближенные законы. Отступления от них носят как количественный, так и качественный характер. Количественные отступления проявляются в том, что уравнение Менделеева-Клапейрона соблюдается для реальных газов лишь приближенно. Реальные газы могут быть переведены в жидкое и твердое состояние. Отступления от законов идеальных газов связаны с тем, что между молекулами газа действуют силы, которые в теории идеальных газов во внимание не принимаются. Это силы: Химические - приводят к образованию химических соединений. Молекулярные - силы взаимодействия между атомами и молекулами, если новые соединения не образуются. Силы кулоновского притяжения и отталкивания между ионами, если газ ионизован.
Реальные газы. Уравнение состояния идеального газа pV = m/M RT годится для описания реальных газовых систем лишь в узкой области температур и давлений: а именно при высоких температурах T, малых давлениях p и, следовательно, для малых плотностей. Вне этого интервала наблюдаются существенные отклонения от поведения, предсказываемого этим уравнением. Так, например, само произведение pV, стоящее в левой части уравнения состояния, становится само зависящим от давления p. Эксперимент показывает следующее. При низких давлениях сжать реальный газ легче, чем идеальный, а при высоких давлениях - реальный газ сжимается труднее идеального. Т.е. опыт показывает, что между молекулами газа существуют силы притяжения и отталкивания. Их необходимо учитывать, чтобы описать поведение газа в более широком интервале. Так, идеальный газ не превращается в жидкость или в твердое тело, а реальные газы испытывают такие превращения, и причина тому - взаимодействие между молекулами Силы и энергия межмолекулярного взаимодействия.
Реальные газы – газы, свойства которых зависят от взаимодействия молекул. В обычных условиях, когда средняя потенциальная энергия межмолекулярного взаимодействия много меньше средней кинетической энергии молекул, свойства реальных и идеальных газов отличаются незначительно. Поведение этих газов резко различно при высоких давлениях и низких температурах, когда начинают проявляться квантовые эффекты. Ван–дер–Ваальс, объясняя свойства реальных газов и жидкостей, предположил, что на малых расстояниях между молекулами действуют силы отталкивания, которые с увеличением расстояния сменяются силами притяжения. Межмолекулярные взаимодействия имеют электрическую природу и складываются из сил притяжения (ориентационных, индукционных) и сил отталкивания. Ориентационные силы действуют между полярными молекулами – молекулами, обладающими дипольными или квадрупольными моментами. Сила притяжения между молекулами зависит от их взаимной ориентации, поэтому они и называются ориентационными. Хаотическое тепловое движение непрерывно меняет ориентацию полярных молекул, но среднее по всем ориентациям значение силы не равно нулю (рис. 7.1).
Среднее значение потенциальной энергии ориентационного межмолекулярного взаимодействия равно Uор(r) ~ p1 p2 r-6, где p1,p2 – дипольные моменты взаимодействующих молекул. Сила ориентационного взаимодействия Fор = – dU/dr ~ r-7 убывает с расстоянием значительно быстрее, чем кулоновская сила взаимодействия заряженных частиц Fкул ~ r– 2. Индукционные (поляризационные) силы действуют между полярной и неполярной молекулами, а также между полярными молекулами. Полярная молекула создает электрическое поле, которое поляризует другую молекулу – индуцирует в ней дипольный момент. Потенциальная энергия межмолекулярного взаимодействия в этом случае пропорциональна дипольному моменту p1 полярной молекулы и поляризуемости α2 второй молекулы: Uинд ~ p1α2 r– 6. Индукционные силы убывают по тому же закону, что и ориентационные Fинд ~ r–7. Дисперсионное молекулярное взаимодействие возникает благодаря виртуальному нарушению электронейтральности молекулы в отдельные моменты времени. Мгновенный диполь поляризует соседние молекулы – возникает взаимодействие мгновенных диполей. Данное взаимодействие называется дисперсионным, его энергия определяется поляризуемостью молекул α1, α2: U(r) ~ α1α2 r–6, а сила убывает по закону Fдисп ~ r–7. Обычно дисперсионные силы превосходят ориентационные и индукционные. Например, при взаимодействии таких полярных молекул, как СО, НI, HBr и др., Fдисп в десятки и сотни раз превосходят все остальные. Отметим, что все три силы и энергии одинаковым образом убывают с расстоянием: F = Fор + Fинд + Fдисп ~ r–7, U = Uор + Uинд + Uдисп ~ r–6. Силы отталкивания действуют между молекулами на очень малых расстояниях, когда происходит взаимодействие электронных оболочек атомов, входящих в состав молекул. Принцип Паули запрещает проникновение заполненных электронных оболочек друг в друга. Возникающие при этом силы отталкивания зависят в большей степени, чем силы притяжения от индивидуальных особенностей молекул. К хорошему согласию с данными экспериментов приводит допущение, что потенциальная энергия сил отталкивания возрастает с уменьшением расстояния по закону Uот(r) ~ r–12, а, соответственно, сила отталкивания растет как Fот ~ r–13. Полагаем, что U(r = ¥) = 0 – при больших расстояниях потенциальная энергия взаимодействия равна нулю. В этом случае кривая взаимодействия описывается потенциалом Леннарда – Джонса (рис. 7.2) U(r) = – ar–6 + br–12.
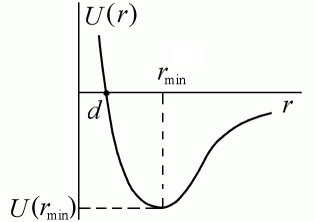
Глубина потенциала равна U(rmin) = –a2/4b при rmin = (2b/a)1/6 – расстоянии, соответствующем наибольшей энергии связи молекул. Отметим, что в данном потенциале не учтены ориентационные взаимодействия, существенные для многоатомных молекул и кристаллов. Эффективный диаметр молекул. Как мы знаем из основных положений молекулярно-кинетической теории молекулы на близких расстояниях отталкиваются друг от друга. Движение двух молекул, летящих навстречу друг другу, проще проанализировать, если использовать закон сохранения механической энергии применительно к этим молекулам. Потенциальная энергия взаимо-действия двух молекул Wn(r) изображена на рис.6.1. На расстоянии r0 потенциальная энергия достигает минимума, а силы взаимодействия обращаются в ноль.
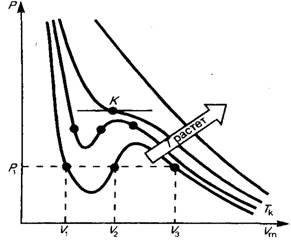
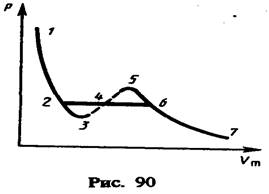
Рис. 6.1 При большом расстоянии между молекулами (r >>r0) Wn = 0, в этом случае их полная энергия W является суммой их кинетических энергий. При сближении молекул сначала, до точки r0, действуют силы притяжения, затем - силы отталкивания. За счет работы сил отталкивания кинетическая энергия молекул уменьшается, и при некотором расстоянии молекулы на мгновение останавливаются. В этот момент времени полная энергия молекул W равна потенциальной энергии их взаимодействия Wn(r). Ясно, что с увеличением полной энергии минимальное расстояние, на которое могут сблизиться молекулы, уменьшается. Так на приведенном рисунке полная энергия W1 больше полной энергииW2. Поэтому расстояние r1, на которое могут сблизиться молекулы с энергией W1, меньше, чем расстояние r2, на которое сближаются молекулы с энергией W2. В случае соударения двух одинаковых шаров минимальное расстояние между центрами шаров равно их диаметру. Поэтому эффективным диаметром молекулы d называют минимальное расстояние, на которое сближаются при соударении центры двух молекул. Ясно, что эффективный диаметр молекулы зависит от скорости их сближения (кинетической энергии на большом расстоянии), а значит - от температуры. Уравнение Ван-дер-Вальса Изотермы Ван-дер-Ваальса и их анализ
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 2609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |


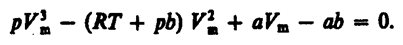
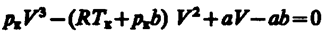 (62.2)
(62.2)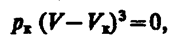 (62.3)
(62.3)