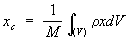Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы кинематики вращательного движения. Угловая скорость и угловое ускорение их связь с линейными скоростями и ускорениями точек вращающегося тела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 6). Ее положение через промежуток времени D t зададим углом D Тангенциальная составляющая ускорения
5. Динамика материальной точки и поступательного движения твёрдого тела. Сила. Закон инерции и инерциальные системы отсчета. Закон динамики материальной точки (2 и 3 законы Ньютона) Динамика рассматривает закон движения тел и причины, вызывающие или изменяющие это движение. Изменение движения тел или изменение их формы происходит в результате взаимодействия по меньшей мере двух тел. Силой называется физическая величина, характеризующая взаимодействие тел; она определяет изменение движения тела или изменение формы тела, или то и другое вместе. Сила – величина векторная. Две силы, действующие на тело, складываются по правилу параллелограмма. Первый закон Ньютона (закон инерции). Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к телу силы не вызовут изменения его состояния. Свойство тел сохранять величину и направление скорости, когда на него не действуют силы или действие сил скомпенсировано, называется инерцией (или инертностью). Инерциальная система отсчёта, система отсчёта, в которой справедлив закон инерции. Всякая система отсчёта, движущаяся по отношению к ИСО поступательно, равномерно и прямолинейно, есть также ИСО. Следовательно, теоретически может существовать сколько угодно равноправных ИСО, обладающих тем важным свойством, что во всех таких системах законы физики одинаковы (так называемый принцип относительности). Помимо закона инерции, в любой ИСО справедливы также 2-й закон Ньютона и законы сохранения количества движения, момента количества движения и движения для замкнутых, т. е. не подверженных внешним воздействиям, систем. Второй закон Ньютона. Ускорение тела в результате действия на него силы F пропорционально величине этой силы и обратно пропорционально массе тела m. Направление силы совпадает с направлением ускорения:
В системе СИ за единицу силы принимают силу, которая телу массой в 1 кг сообщает ускорение 1 м/c2. Эту единицу называют ньютоном (Н) Третий закон Ньютона. Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.
Закон сохранения импульса и его применение при воздействии на систему материальных точек только внутренних сил; только внешних сил. Центр масс механической системы. Координаты центра масс и закон его движения. Закон сохранения импульса и его применение. Если сумма внешних сил, действующих на систему, равна нулю, то равно нулю и изменение импульса системы: Центр масс механической системы. Координаты центра масс и закон его движения. Центр масс- геометрическая точка, положение которой характеризует распределение масс в телеили механической системе. Координаты Ц. м. определяются формулами
или для тела при непрерывном распределении масс
где mк — массы материальных точек, образующих систему, xk, ук, zk — координаты этих точек, М =Σ mк— масса системы, ρ — плотность, V — объём. Понятие о Ц. м. отличается от понятия о центре тяжести тем, что последнее имеет смысл только для твёрдого тела, находящегося в однородном полетяжести; понятие же о Ц. м. не связано ни с каким силовым полем и имеет смысл для любой механическойсистемы. Для твёрдого тела положения Ц. м. и центра тяжести совпадают. При движении механической системы её Ц. м. движется так, как двигалась бы материальная точка,имеющая массу, равную массе системы, и находящаяся под действием всех внешних сил, приложенных ксистеме. Кроме того, некоторые уравнения движения механической системы (тела) по отношению к осям,имеющим начало в Ц. м. и движущимся вместе с Ц. м. поступательно, сохраняют тот же вид, что и длядвижения по отношению к инерциальной системе отсчёта.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 2589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 . Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются
. Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются 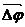 или
или 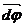 ). Модуль вектора
). Модуль вектора 

 направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор
направлен вдоль оси вращения по правилу правого винта, т.е. так же, как и вектор 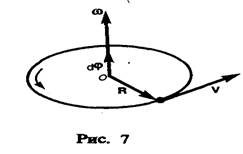
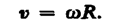


 , а направление совпадает с направлением поступательного движения правого винта при его вращении от
, а направление совпадает с направлением поступательного движения правого винта при его вращении от  = const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени D t = T соответствует
= const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени D t = T соответствует  = 2p, то
= 2p, то 



 сонаправлен вектору
сонаправлен вектору 



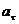 , нормальное ускорение
, нормальное ускорение  ) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами:
) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами: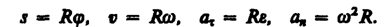
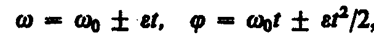


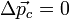 . Это означает, что, какой бы интервал времени мы ни взяли, суммарный импульс в начале этого интервала
. Это означает, что, какой бы интервал времени мы ни взяли, суммарный импульс в начале этого интервала 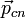 и в его конце
и в его конце  один и тот же:
один и тот же:  . Импульс системы остается неизменным, или, как говорят, сохраняется:
. Импульс системы остается неизменным, или, как говорят, сохраняется: . (10)
. (10)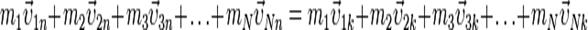 . (11)
. (11)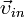 — скорости тел в начальный момент времени, а
— скорости тел в начальный момент времени, а  — в конечный. Так как импульс — величина векторная, то уравнение (11) представляет собой компактную запись трех уравнений для проекций импульса системы на координатные оси.
— в конечный. Так как импульс — величина векторная, то уравнение (11) представляет собой компактную запись трех уравнений для проекций импульса системы на координатные оси.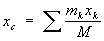 ,
,