Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механическое движение как простейшая форма движения материи. Преставления о формах пространства и времени, лежащие в основе классической механики. Границы применимости классической механики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Механическое движение как простейшая форма движения материи. Преставления о формах пространства и времени, лежащие в основе классической механики. Границы применимости классической механики. Простейшей формой движения материи является механическое движение, которое состоит в перемещении тел или их частей друг относительно друга. Совокупность тел, выделенная для рассмотрения, называется механической системой. Какие тела следует включить в систему, зависит от характера решаемой задачи. Если мы собираемся изучать движение какого-либо тела, то обязательно нужно указать, по отношению к каким другим телам происходит данное движение. Движение происходит как в пространстве, так и во времени (пространство и время — неотъемлемые формы существования материи). Поэтому для описания движения необходимо также определять время. Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образует систему отсчета. Описать движение тела означает указать для каждого момента времени положение в пространстве и скорость тела. Для того чтобы задать состояние механической системы, нужно указать положения и скорости всех тел, образующих систему. Тело, размерами которого в условиях данной задачи, можно пренебречь, называется материальной точкой. Абсолютно твердым телом называется тело, деформациями которого можно в условиях данной задачи пренебречь. Всякое движение твердого тела можно разложить на два основных вида движения — поступательное и вращательное. Поступательное движение — это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе (рис. 1.1).
Ось вращения может находиться вне тела (см. рис. 1.2, б).
Однородность пространства состоит в том, что одинаковые физические явления в одних и тех же условиях совершаются одинаково в различных частях пространства. Все точки пространства, таким образом, совершенно неразличимы, равноправны и любая из них может быть принята за начало системы координат. Однородность пространства проявляется в законе сохранения импульса. Пространство обладает еще и изотропностью: одинаковостью свойств во всех направлениях. Изотропность пространства проявляется в законе сохранения момента импульса Однородность времени проявляется в законе сохранения энергии. Механику, изучающую движение макротел со скоростями намного меньшими скорости света в вакууме, называют классической. Пространство, имеющее три измерения, подчиняется эвклидовой геометрии, то есть является плоским. Все инерциальные системы отсчета эквивалентны друг другу в механическом отношении. В классической механике соблюдается принцип дальнодействия: взаимодействия тел, распространяются мгновенно, то есть с бесконечно большой скоростью. Классическая механика Ньютона изучает медленное движение(<<с) макроскопических тел. Элементы кинематики материальной точки. Скорость и ускорение точки, как производные радиуса вектора по времени. Кинематика изучает движение тел, не рассматривая причин, вызывающих это движение. Простым движущимся телом является материальная точка. Материальной точкой называется тело, размерами которого можно пренебречь при описании его движения. Например, годичное движение Земли вокруг солнца можно представить, как движение материальной точки, а суточное движение Земли вокруг своей оси - уже нельзя. Всякое твёрдое тело можно рассматривать как систему жёстко связанных тел друг с другом материальных точек. Линия, описываемая движущейся материальной точкой, называется траекторией. Движения разделяются по виду траекторий на прямолинейные и криволинейные. По своему характеру движение может быть равномерным и переменным. Закон сохранения импульса и его применение при воздействии на систему материальных точек только внутренних сил; только внешних сил. Центр масс механической системы. Координаты центра масс и закон его движения. Закон сохранения импульса и его применение. Если сумма внешних сил, действующих на систему, равна нулю, то равно нулю и изменение импульса системы: Центр масс механической системы. Координаты центра масс и закон его движения. Центр масс- геометрическая точка, положение которой характеризует распределение масс в телеили механической системе. Координаты Ц. м. определяются формулами
или для тела при непрерывном распределении масс
где mк — массы материальных точек, образующих систему, xk, ук, zk — координаты этих точек, М =Σ mк— масса системы, ρ — плотность, V — объём. Понятие о Ц. м. отличается от понятия о центре тяжести тем, что последнее имеет смысл только для твёрдого тела, находящегося в однородном полетяжести; понятие же о Ц. м. не связано ни с каким силовым полем и имеет смысл для любой механическойсистемы. Для твёрдого тела положения Ц. м. и центра тяжести совпадают. При движении механической системы её Ц. м. движется так, как двигалась бы материальная точка,имеющая массу, равную массе системы, и находящаяся под действием всех внешних сил, приложенных ксистеме. Кроме того, некоторые уравнения движения механической системы (тела) по отношению к осям,имеющим начало в Ц. м. и движущимся вместе с Ц. м. поступательно, сохраняют тот же вид, что и длядвижения по отношению к инерциальной системе отсчёта. Потенциальная энергия. Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил. Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное. ЕП1 - ЕП2 = ЕП = А12конс, Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.
Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень. Применение законов сохранения к абсолютно неупругому удару. Энергия идущая на деформацию. Примеры неупругого удара. Абсолютно неупругий удар, характеризуется тем, что потенциальной энергии деформации не возникает; кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса, закон же сохранения механической энергии не соблюдается: имеет место закон сохранения суммарной энергии различных видов — механической и внутренней. В силу закона сохранения суммарный импульс частиц после удара должен быть таким же, как и до удара:
где v - скорость движения шаров после удара. Тогда
Абсолютно неупругий удар - это пример потери механической энергии под действием диссипативных сил. Релятивистский импульс Он равен произведению релятивистской массы на скорость
Основное уравнение релятивистской динамики имеет вид
В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: "релятивистский импульс замкнутой системы сохраняется". Из этого закона следует закон сохранения релятивистской массы: "полная релятивистская масса замкнутой системы сохраняется". Закон сложения скоростей
В случае движения частицы параллельно осям ОХ и O'X- в направлении скорости
Эта формула выражает закон сложения скоростей в релятивистской механике. При Или пусть
Идеальный газ как модель. Основное уравнение мкт идеального газа для давления и его сравнение с уравнение Менделеева-Клайперона. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование температуры. Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура). В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Это уравнение связывает макропараметры системы – давление p и концентрацию молекул
Вывод этого уравнения основан на представлениях о том, что молекулы идеального газа подчиняются законам классической механики, а давление – это отношение усредненной по времени силы, с которой молекулы бьют по стенке, к площади стенки. Пропорциональность силы, с которой молекулы воздействуют на стенку, их концентрации, массе и скорости каждой молекулы качественно понятны. Квадратичный рост давления со скоростью связан с тем, что от скорости зависит не только сила отдельного удара, но и частота соударений молекул со стенкой. Учитывая связь между концентрацией молекул в газе и его плотностью ( = nm 0), можно получить еще одну форму основного уравнения МКТ идеального газа:
Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа) В результате экспериментальных исследований многих ученых было установлено, что макропараметры реальных газов не могут изменяться независимо. Они связаны уравнением состояния: pV = vRT где R = 8,31 Дж/(K·моль) – универсальная газовая постоянная,
Температура, как мера средней кинетической энергии молекул Попробуем получить нетривиальные результаты, используя уравнение Клайперона-Менделеева и основное уравнение МКТ. Введем понятие средней кинетической энергии молекул:
Преобразуем основное уравнение МКТ с учетом формулы (1):
Воспользуемся уравнением К.-М. в таком виде:
Сравним уравнения (2) и (3) и получим, что
Как понимать формулу (4)? Мы выяснили, что от температуры зависит величина средней кинетической энергии молекул. Поэтому говорят, что температура - мера средней кинетической энергии молекул. Это утверждение мы доказали на для идеального газа, но оказывается оно справедливо и для других агрегатных сосятояний вещества. Молекулярно – кинетическое толкование абсолютной температуры. C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия <εk>хаотического движения молекул (T~<εk>). Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой <εk>=3/2kT где k - постоянная Больцмана, k=1.38*10-23 (Дж/К). Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы. Формула позволяет выяснить смысл абсолютного нуля: T=0, если < εk > =0. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул. Рис.1 Относительное число молекул dN(ν)/N, со скоростями, лежащими в интервале от ν до ν +d ν, рассчитывается как площадь заштрихованной полоски на рис. 1. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция f(ν) удовлетворяет условию нормировки
Скорость, при которой максимальна функция распределения молекул идеального газа по скоростям, называется наиболее вероятной скоростью, значение которой можно найти продифференцировав выражение (1) (постоянные множители опускаем) по аргументу ν, при этом приравняв результат нулю и используя условие для максимума выражения f(ν):
Значения ν =0 и ν =∞ соответствуют минимумам выражения (1), а значение ν, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость ν B:
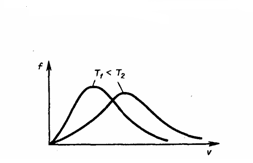
Из формулы (2) мы видим, что при возрастании температуры максимум функции распределения молекул по скоростям (рис. 2) движется вправо (при этом становится больше значение наиболее вероятной скорости). Однако площадь, которая ограничена кривой, не меняется, поэтому кривая распределения молекул по скоростям при повышении температуры будет растягиваться и понижаться.
Рис.2
Подставляя сюда f(ν) и интегрируя, получаем
Скорости, которые характеризуют состояние газа: 1) наиболее вероятная
найдем распределение молекул газа по значениям кинетической энергии ε. С этой целью перейдем от переменной ν к переменной ε=m0v2/2. Подставив в (4)
где dN(ε) — число молекул, которые имели кинетическую энергию поступательного движения, заключенную в интервале от ε до ε + dε. Значит, функция распределения молекул по энергиям теплового движения
Средняя кинетическая энергия <ε> молекулы идеального газа
т. е. получили результат, совпадающий с формулой о средней кинетической энергии движения одной молекулы идеального газа, выводимой из молекулярно-кинетической теории.
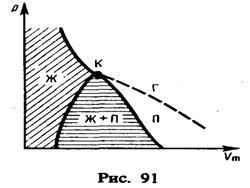
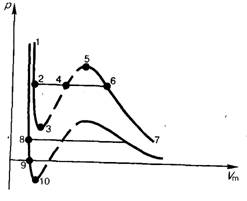
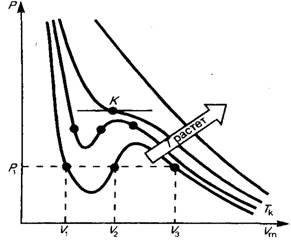
Изображение щели получается размытым. Исследуя толщину осаждённого слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению. Уравнение Ван-дер-Вальса Изотермы Ван-дер-Ваальса и их анализ
Механическое движение как простейшая форма движения материи. Преставления о формах пространства и времени, лежащие в основе классической механики. Границы применимости классической механики. Простейшей формой движения материи является механическое движение, которое состоит в перемещении тел или их частей друг относительно друга. Совокупность тел, выделенная для рассмотрения, называется механической системой. Какие тела следует включить в систему, зависит от характера решаемой задачи. Если мы собираемся изучать движение какого-либо тела, то обязательно нужно указать, по отношению к каким другим телам происходит данное движение. Движение происходит как в пространстве, так и во времени (пространство и время — неотъемлемые формы существования материи). Поэтому для описания движения необходимо также определять время. Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образует систему отсчета. Описать движение тела означает указать для каждого момента времени положение в пространстве и скорость тела. Для того чтобы задать состояние механической системы, нужно указать положения и скорости всех тел, образующих систему. Тело, размерами которого в условиях данной задачи, можно пренебречь, называется материальной точкой. Абсолютно твердым телом называется тело, деформациями которого можно в условиях данной задачи пренебречь. Всякое движение твердого тела можно разложить на два основных вида движения — поступательное и вращательное. Поступательное движение — это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе (рис. 1.1).
Ось вращения может находиться вне тела (см. рис. 1.2, б).
Однородность пространства состоит в том, что одинаковые физические явления в одних и тех же условиях совершаются одинаково в различных частях пространства. Все точки пространства, таким образом, совершенно неразличимы, равноправны и любая из них может быть принята за начало системы координат. Однородность пространства проявляется в законе сохранения импульса. Пространство обладает еще и изотропностью: одинаковостью свойств во всех направлениях. Изотропность пространства проявляется в законе сохранения момента импульса Однородность времени проявляется в законе сохранения энергии.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 2807; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.047 с.) |

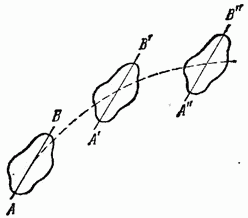 При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения (рис. 1.2).
При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения (рис. 1.2).
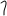 Пространство однородно и изотропно, а время - однородно.
Пространство однородно и изотропно, а время - однородно.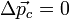 . Это означает, что, какой бы интервал времени мы ни взяли, суммарный импульс в начале этого интервала
. Это означает, что, какой бы интервал времени мы ни взяли, суммарный импульс в начале этого интервала 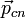 и в его конце
и в его конце  один и тот же:
один и тот же:  . Импульс системы остается неизменным, или, как говорят, сохраняется:
. Импульс системы остается неизменным, или, как говорят, сохраняется: . (10)
. (10)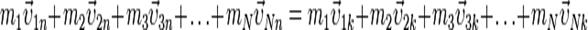 . (11)
. (11)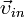 — скорости тел в начальный момент времени, а
— скорости тел в начальный момент времени, а  — в конечный. Так как импульс — величина векторная, то уравнение (11) представляет собой компактную запись трех уравнений для проекций импульса системы на координатные оси.
— в конечный. Так как импульс — величина векторная, то уравнение (11) представляет собой компактную запись трех уравнений для проекций импульса системы на координатные оси.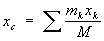 ,
, 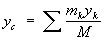
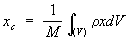
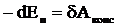 .
.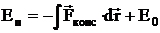 .
.
 (15.10)
(15.10) 


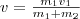

 . (18)
. (18)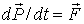 или
или 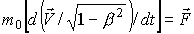 . (19)
. (19)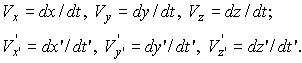
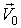
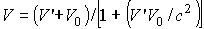 . (16)
. (16)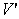 =c, из (16) найдем, что
=c, из (16) найдем, что 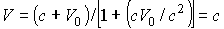 .
. , где
, где 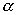 - малая величина, то
- малая величина, то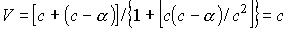 .
. с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:
с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:
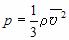
 , где m – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:
, где m – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:
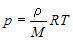
 (1)
(1)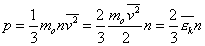 т.е. основное уравнение МКТ запишем так
т.е. основное уравнение МКТ запишем так  (2)
(2) (3)
(3) или
или  (4)
(4)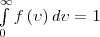
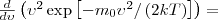

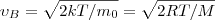 (2)
(2)

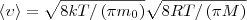 (3)
(3)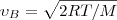 2) средняя
2) средняя 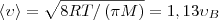 3) средняя квадратичная
3) средняя квадратичная 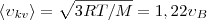 (рис. 1). Исходя из распределения молекул по скоростям
(рис. 1). Исходя из распределения молекул по скоростям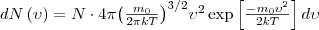 (4)
(4) и
и 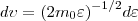 , получим
, получим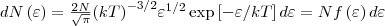
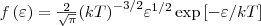
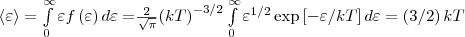
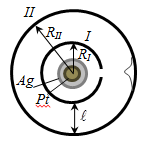 Вдоль оси внутреннего цилиндра с целью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током. При нагревании серебро испаряется, атомы серебра вылетают через щель и попадают на внутреннюю поверхность второго цилиндра. Если оба цилиндра неподвижны, то все атомы независимо от их скорости попадают в одно и то же место В. При вращении цилиндров с угловой скоростью ω атома серебра попадут в точки В’, B’’ и так далее. По величине ω, расстоянию? и смещению х = ВВ’ можно вычислить скорость атомов, попавших в точку В’.
Вдоль оси внутреннего цилиндра с целью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током. При нагревании серебро испаряется, атомы серебра вылетают через щель и попадают на внутреннюю поверхность второго цилиндра. Если оба цилиндра неподвижны, то все атомы независимо от их скорости попадают в одно и то же место В. При вращении цилиндров с угловой скоростью ω атома серебра попадут в точки В’, B’’ и так далее. По величине ω, расстоянию? и смещению х = ВВ’ можно вычислить скорость атомов, попавших в точку В’.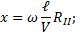
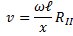
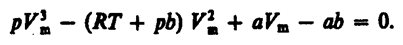
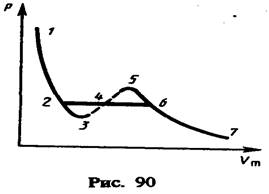
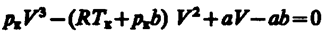 (62.2)
(62.2)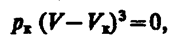 (62.3)
(62.3)