
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Термодинамический и молекулярно-кинетический методы исследования. Термодинамические параметры. Равновесные состояния и процессы, и их изображение на термодинамической диаграмме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Термодинамические и молекулярно-кинетический методы исследования. Для исследования физических свойств макроскопических систем, связанных с огромным числом содержащихся в них атомов и молекул, применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (или молекулярно-кинетический) и термодинамический. Статистический метод — это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними (усредненными) значениями физических величин, характеризующих всю систему. Этот метод лежит в основе молекулярной физики — раздела физики, изучающего строение и свойства вещества исходя из молекулярно- кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении. В дальнейшем мы будем использовать термин "молекула" имея ввиду мельчайшую структурную единицу (элемент) данного вещества. Термодинамический метод — это метод исследования систем из большого числа частиц, оперирующий величинами, характеризующими систему в целом (например, давление, объем, температура) при различных превращениях энергии, происходящих в системе, не учитывая при этом внутреннего строения изучаемых тел и характера движения отдельных частиц. Этот метод лежит в основе термодинамики — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.
Термодинамические параметры. Параметры состояния, термодинамические параметры — физические величины, характеризующие состояние термодинамической системы: температура, давление, удельный объём, намагниченность,электрическая поляризация и др. Различают экстенсивные параметры состояния, пропорциональныемассе системы: объём, внутренняя энергия, энтропия, энтальпия, энергия Гиббса, энергия Гельмгольца (свободная энергия), и интенсивные параметры состояния, не зависящие от массы системы: давление, температура, концентрация, магнитная индукция и др. Не все параметры состояния независимы, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния.
Равновесные состояния и процессы, и их изображение. Равновесные состояния и процессы, их изображение на термодинамических диаграммах. Равновесные процессы: T-const-изотермический процесс.
P=const-изобарный. V=const-изохорный. Идеальный газ как модель. Основное уравнение мкт идеального газа для давления и его сравнение с уравнение Менделеева-Клайперона. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование температуры. Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура). В результате каждого столкновения между молекулами и молекул со стенками скорости молекул могут изменяться по модулю и по направлению; на интервалах времени между последовательными столкновениями молекулы движутся равномерно и прямолинейно. В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, т. е. подчиняются законам механики Ньютона.
Это уравнение связывает макропараметры системы – давление p и концентрацию молекул
Вывод этого уравнения основан на представлениях о том, что молекулы идеального газа подчиняются законам классической механики, а давление – это отношение усредненной по времени силы, с которой молекулы бьют по стенке, к площади стенки. Пропорциональность силы, с которой молекулы воздействуют на стенку, их концентрации, массе и скорости каждой молекулы качественно понятны. Квадратичный рост давления со скоростью связан с тем, что от скорости зависит не только сила отдельного удара, но и частота соударений молекул со стенкой. Учитывая связь между концентрацией молекул в газе и его плотностью ( = nm 0), можно получить еще одну форму основного уравнения МКТ идеального газа:
Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа) В результате экспериментальных исследований многих ученых было установлено, что макропараметры реальных газов не могут изменяться независимо. Они связаны уравнением состояния: pV = vRT где R = 8,31 Дж/(K·моль) – универсальная газовая постоянная,
Температура, как мера средней кинетической энергии молекул Попробуем получить нетривиальные результаты, используя уравнение Клайперона-Менделеева и основное уравнение МКТ. Введем понятие средней кинетической энергии молекул:
Преобразуем основное уравнение МКТ с учетом формулы (1):
Воспользуемся уравнением К.-М. в таком виде:
Сравним уравнения (2) и (3) и получим, что
Как понимать формулу (4)? Мы выяснили, что от температуры зависит величина средней кинетической энергии молекул. Поэтому говорят, что температура - мера средней кинетической энергии молекул. Это утверждение мы доказали на для идеального газа, но оказывается оно справедливо и для других агрегатных сосятояний вещества. Молекулярно – кинетическое толкование абсолютной температуры. C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия <εk>хаотического движения молекул (T~<εk>). Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой <εk>=3/2kT где k - постоянная Больцмана, k=1.38*10-23 (Дж/К). Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы. Формула позволяет выяснить смысл абсолютного нуля: T=0, если < εk > =0. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |




 с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:
с ее микропараметрами – массой молекул, их средним квадратом скорости или средней кинетической энергией:
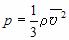
 , где m – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:
, где m – масса газа и M – молярная масса газа. Уравнение Менделеева – Клапейрона называют уравнением состояния, поскольку оно связывает функциональной зависимостью параметры состояния. Его записывают и в других видах:
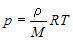
 (1)
(1)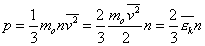 т.е. основное уравнение МКТ запишем так
т.е. основное уравнение МКТ запишем так  (2)
(2) (3)
(3) или
или  (4)
(4)


