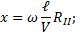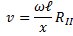Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон максвелла для распределения молекул идеального газа по скоростям. Наиболее вероятная квадратичная и средняя арифметическая скорости молекул. Опытное подтверждение.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте При выводе основного уравнения молекулярно-кинетической теории полагалось, что молекулы имеют различные скорости. После многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Но из-за хаотического движения молекул все направления движения равновероятны, т. е. в любом направлении в среднем движется равное число молекул. Согласно молекулярно-кинетической теории, как бы ни изменялись при столкновениях скорости молекул, средняя квадратичная скорость молекул массой m0 в газе, который находится в состоянии равновесия при Т= const, остается неизменно и равной Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем статистическое распределение молекул по скоростям, подчиняющаяся вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом. При выводе закона распределения молекул по скоростям Максвелл сделал предположение, что газ состоит из огромного числа N тождественных молекул, которые находятся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют. Закон Максвелла описывается некоторой функцией f(ν), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν +d ν, т. е.
откуда
Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям:
Из (1) видно, что конкретный вид функции зависит от вида газа (от массы молекулы) и от параметра состояния (от температуры Т). График функции (1) приведен на рис. 1. Так как при возрастании ν множитель exp[–m0 ν 2/(2kT)] уменьшается быстрее, чем увеличивается множитель ν 2, то функция f(ν), начинаясь от нуля, достигает максимума при ν B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно ν B.
Рис.1 Относительное число молекул dN(ν)/N, со скоростями, лежащими в интервале от ν до ν +d ν, рассчитывается как площадь заштрихованной полоски на рис. 1. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция f(ν) удовлетворяет условию нормировки
Скорость, при которой максимальна функция распределения молекул идеального газа по скоростям, называется наиболее вероятной скоростью, значение которой можно найти продифференцировав выражение (1) (постоянные множители опускаем) по аргументу ν, при этом приравняв результат нулю и используя условие для максимума выражения f(ν):
Значения ν =0 и ν =∞ соответствуют минимумам выражения (1), а значение ν, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость ν B:
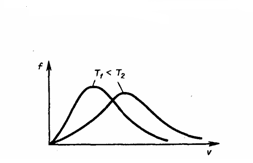
Из формулы (2) мы видим, что при возрастании температуры максимум функции распределения молекул по скоростям (рис. 2) движется вправо (при этом становится больше значение наиболее вероятной скорости). Однако площадь, которая ограничена кривой, не меняется, поэтому кривая распределения молекул по скоростям при повышении температуры будет растягиваться и понижаться.
Рис.2
Подставляя сюда f(ν) и интегрируя, получаем
Скорости, которые характеризуют состояние газа: 1) наиболее вероятная
найдем распределение молекул газа по значениям кинетической энергии ε. С этой целью перейдем от переменной ν к переменной ε=m0v2/2. Подставив в (4)
где dN(ε) — число молекул, которые имели кинетическую энергию поступательного движения, заключенную в интервале от ε до ε + dε. Значит, функция распределения молекул по энергиям теплового движения
Средняя кинетическая энергия <ε> молекулы идеального газа
т. е. получили результат, совпадающий с формулой о средней кинетической энергии движения одной молекулы идеального газа, выводимой из молекулярно-кинетической теории.
Изображение щели получается размытым. Исследуя толщину осаждённого слоя, можно оценить распределение молекул по скоростям, которое соответствует максвелловскому распределению.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1255; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |



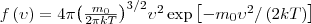 (1)
(1)
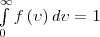
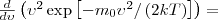

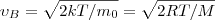 (2)
(2)

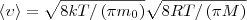 (3)
(3)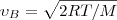 2) средняя
2) средняя 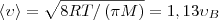 3) средняя квадратичная
3) средняя квадратичная 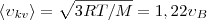 (рис. 1). Исходя из распределения молекул по скоростям
(рис. 1). Исходя из распределения молекул по скоростям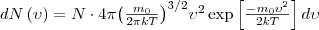 (4)
(4) и
и 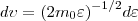 , получим
, получим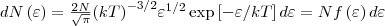
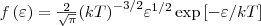
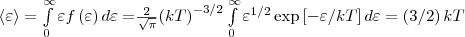
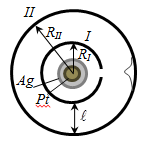 Вдоль оси внутреннего цилиндра с целью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током. При нагревании серебро испаряется, атомы серебра вылетают через щель и попадают на внутреннюю поверхность второго цилиндра. Если оба цилиндра неподвижны, то все атомы независимо от их скорости попадают в одно и то же место В. При вращении цилиндров с угловой скоростью ω атома серебра попадут в точки В’, B’’ и так далее. По величине ω, расстоянию? и смещению х = ВВ’ можно вычислить скорость атомов, попавших в точку В’.
Вдоль оси внутреннего цилиндра с целью натянута платиновая проволока, покрытая слоем серебра, которая нагревается током. При нагревании серебро испаряется, атомы серебра вылетают через щель и попадают на внутреннюю поверхность второго цилиндра. Если оба цилиндра неподвижны, то все атомы независимо от их скорости попадают в одно и то же место В. При вращении цилиндров с угловой скоростью ω атома серебра попадут в точки В’, B’’ и так далее. По величине ω, расстоянию? и смещению х = ВВ’ можно вычислить скорость атомов, попавших в точку В’.