
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема № 4 Молекулярная физика.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
4.1 Молекулярно-кинетическая теория
Идея об атомном строении вещества возникла в глубокой древности, однако молекулярно-кинетическая теория (МКТ) в окончательном виде была построена в XIX веке. Обоснованием этой теории послужили закон кратных отношений в химии, работы Авогадро, Ломоносова, Максвелла, Больцмана и др. Убедительным доказательством МКТ является броуновское движение открытое английским ботаником Броуном в 1827 г., которое заключается в том, что все мельчайшие частицы, взвешенные в жидкости, находятся в непрерывном дрожании. Взвешенными называются макроскопические тела, которые падают в вязкой среде со скоростью, практически незаметной для человеческого глаза. Будем считать для простоты, что частица имеет форму шара радиусом а, с плотностью ρ, которая больше плотности среды ρ0. На неё действуют сила тяжести, сила Архимеда и сила сопротивления среды. Сила тяжести направлена вниз, остальные две силы – вверх. Сумму сил тяжести и Архимеда называют кажущимся весом P* = mg ̶ ρ0gm/ρ = mg(1 ̶ ρ0/ρ) (4.1) Т.к. сила сопротивления среды зависит от скорости частицы. То через определенный промежуток времени движение частицы становится равномерным. Скорость установившегося движения частицы зависит от её радиуса а. Если считать, что сила сопротивления пропорциональна площади сечения частицы (~ а 2) и её скорости v, а масса пропорциональна а 3. то скорость установившегося движения частицы пропорциональна её радиусу, т.е. чем меньше размеры частицы, тем медленнее она падает. Броуновское движение никогда не прекращается. Оно было обнаружено в жидких включениях кварца, которым тысячи лет. Интенсивность броуновского движения возрастает при увеличении температуры и уменьшении вязкости жидкости. Теория броуновского движения была разработана в начале ХХ века Эйнштейном и Смолуховским. Наиболее простым агрегатным состоянием вещества является газообразное. Для описания состояния газа используются такие физические величины, как давление, объём и температура. Давление в механике определяется как отношение модуля силы, действующей перпендикулярно некоторой площадке к площади S этой площадки:
Р = Fn/S (4.2)
Единицей измерения давления в системе СИ является паскаль (Па). Давление атмосферы было измерено в начале XVII Э.Торричелли по высоте поднятия ртути в вертикальной трубке, введённая тогда единица измерения давления – мм рт. ст. используется и в настоящее время. 1 мм рт. ст. Для выяснения молекулярно- кинетического смысла давления рассмотрим очень упрощенную модель газа. Будем считать, что все молекулы имеют одинаковую скорость v и могут двигаться только вдоль трех координатных осей в положительном и отрицательном направлениях. Кроме этого, будем считать, что молекулы сталкиваются только со стенками сосуда, а друг с другом не сталкиваются. Силы притяжения между молекулами учитывать не будем. В этом приближении в положительном направлении.например, оси Х, перпендикулярной одной из стенок, будет перемещаться 1/6 часть всех молекул. Выделим на этой стенке площадку ΔS, за промежуток времени Δt об эту площадку ударится 1/6 ΔS v Δt n молекул (n-концентрация молекул), каждая из которых сообщит площадке импульс 2 mv (m-масса одной молекулы). Тогда давление равно отношению суммарного импульса, сообщенного площадке ΔS к Δt и ΔS
Р = 1/3 n m v2 (4.3)
Т.к. кинетическая энергия одной молекулы εк = mv2/2, то формула (4.3) примет вид:
Р = 2/3 n εк (4.4)
Соотношение (4.4) называют иногда основным уравнением молекулярно-кинетической теории. Если учесть, что молекулы имеют разные скорости и сталкиваются друг с другом, то получается такая же формула, только под εк понимается средняя кинетическая энергия поступательного движения одной молекулы. Это обстоятельство, конечно, не оправдывает простоту рассматриваемой модели газа. Если в этих же предположениях определить число ударов молекул z об единицу площади стенки в единицу времени, то получится формула
z = 1/6n v (4.5)
В точной формуле, полученной с учётом того, что все молекулы имеют разные скорости и сталкиваются друг с другом, численный множитель равен 1/4. Выясним теперь молекулярно-кинетический смысл температуры. Для этого умножим (4.4) на объём V:
P V = 2/3 N Ек (4.6) Таким образом произведение давления на объём пропорционально средней кинетической энергии поступательного движения молекул газа. С другой стороны. Для идеального газа справедливо уравнение Клапейрона –Менделеева:
Р V = ν RT (4.7)
Сравнивая формулы (4.6) и (4.7) можно сделать однозначный вывод о том, что произведение давления и объёма для данной массы газа определяется с одной стороны температурой газа, а с другой стороны – кинетической энергией поступательного движения молекул, поэтому кинетическую энергию 1. Температура –макроскопический параметр, характеризующий термодинамическую систему в состоянии термодинамического равновесия, т. Е. нет смысла спрашивать о температуре одной молекулы или температуре кипятка, в котором плавает кусок льда. 2. С точки зрения МКТ температура характеризует интенсивность теплового движения молекул, например для идеального газа она пропорциональна кинетической энергии поступательного движения молекул. 3. Для количественного измерения температуры используются температурные шкалы. Шкала Цельсия строится по двум реперным точкам – нормальной точке плавления льда и нормальной точке кипения воды. Нормальная точка плавления льда – равновесная температура чистого льда и насыщенной воздухом воды при нормальном давлении (760 мм рт. ст.). Вторая точка – температура кипения воды при нормальном давлении. Первой точке присваивается температура 0 0С, - второй – 100 0С. Удобно за меру температуры взять величину
Θ = 2/3
При этом формула (4.6) принимает вид
PV = N Θ, (4.9)
напоминающий уравнение Клапейрона-Менделеева. Величина Θ называется энергетической температурой и должна измеряться в джоулях, однако о историческим причинам для измерения температуры в термодинамике используется кельвин (К). Отношение Θ/T называется постоянной Больцмана k=1,38 10‒23 Дж/К. Основное уравнение МКТ теперь принимает вид:
P = n kT (4.10)
4.2 Статистические распределения.
При тепловом движении в состоянии термодинамического равновесия все направления скоростей молекул равновероятны, но модули всех скоростей молекул не могут быть одинаковыми, т.к. молекулы часто сталкиваются друг с другом. Задача о распределении молекул газа по скоростям была решена в 1859 г. Максвеллом. Примем произвольную точку пространства О за начало координат, отложим от неё в некоторый момент времени векторы скоростей всех молекул газа. Концы векторов образуют пространство скоростей. Возьмём в пространстве скоростей малый элемент объёма, имеющий, например, форму прямоугольного параллелепипеда с рёбрами dvх, dvу, dvz и с центром в точке vх, vу, vz. Объём этого параллелепипеда равен dω = dvх dvу dvz, число скоростных точек в нём обозначим через dN. Среднее значение
Величина f(v) называется функцией распределения молекул по скоростям. Если
Приведём без вывода вид функции распределения, полученный Максвеллом:
f(v) = 4π (m/(2πkT))3/2 v2 exp (‒ mv2/(2kT)) (4.13)
Прямое измерение скоростей молекул в атомном пучке впервые было проведено в 1920 г. О. Штерном в опытах, ставших классическими. Упрощённая схема опыта изображена на рис.4.2. Платиновая нить А, покрытая серебром, располагалась вдоль оси цилиндра С. Пространство внутри цилиндра D1 откачивалось до давления порядка 10-5 мм рт. ст. При С пропускании электрического тока нить А разогрева- А. D лась, серебро испарялось и его атомы через узкую щель В В двигались равномерно и прямолинейно к цилиндру С и при конденсации на его поверхности образовывали узкую полоску D. При вращении системы с большой скоростью на цилиндре С появлялось размытое изобра- Рис.4.2 жение щели D1, что указывает на то, что атомы серебра Двигаются с различными скоростями. Полученные при обработке результатов значения скорости в пределах погрешностей совпадали с результатами вычислений по формулам Максвелла.
Pассмотрим идеальный газ в однородном поле тяжести при постоянной температуре. Рассмотрим вертикально расположенный цилиндрический столб h газа площадью S. В этом цилиндре выделим объём толщиной dh, находящийся на высоте h. Для его равновесий необходимо, чтобы разность давлений снизу и сверху уравновешивала вес газа в выделеном dh объёме, т.е. ‒ dP S = n mg S dh, где n – концентрация молекул на высоте h. При постоянной температуре g S из (4.10) dP = kT dn и после разделения переменных получаем
dn/n = ‒mg dh/kT (4.14)
После интегрирования с начальными условиями n = n0 при h = 0 получаем:
ln(n/n0) = ‒ mgh/kT (4.15)
и после потенциирования получаем распределение Больцмана:
n = n0 exp (‒ mgh/kT) (4.16)
Для изменения давления из (4.16) получаем барометрическую формулу:
P = P0 exp (‒ Мgh/RT) (4.17)
Применим распределение Больцмана к уединенной планете, окружённой изотермической газовой атмосферой. Потенциальная энергия молекулы с учётом закона всемирного тяготения на расстоянии r равна Еп =
Распределение Больцмана принимает вид
n = n0 exp (GMm/(rkT)) (4/.19)
Как видно из (4.19) на бесконечном расстоянии от планеты Концентрация не равна нулю. Это является следствием того, что атмосфера не равновесна. Молекулы, имеющие скорости большие второй космической скорости, могут покидать атмосферу. Для массивных планет процесс рассеивания атмосферы происходит крайне медленно В учебнике Д. В. Сивухина подробно исследован этот процесс., в частности там приводятся результаты расчёта температуры газа (К), при которой концентрация молекул различных газов уменьшается в e раз за время τ = 1010 лет, которое больше чем в 2 раза превышает возраст Земли.
Из таблицы видно, что Земля надёжно удерживает в атмосфере все газы, кроме водорода и гелия, а Луна практически лишена атмосферы. Рассмотрим явления переноса в газах. В эту группу явлений включают внутреннее трение. диффузию и теплопроводность. Объединяет эти явления механизм передачи каких-либо микроскопических характеристик молекул, - через столкновения\ молекул друг с другом. Для количественного описания этих явлений Клаузиус ввёл понятие средней длины свободного пробега, т.е. среднего расстояния, которое пролетает молекула от одного столкновения до следующего. Для упрощения задачи предположим, что движется только одна молекула с постоянной скоростью v, а остальные молекулы неподвижны Назовём эффективным диаметром молекулы d минимальное расстояния между центрами масс сталкивающихся молекул. Вообразим, что с движущейся молекулой жестко связана сфера радиуса d, эта сфера при движении молекулы описывает ломаный цилиндр, очевидно, что движущаяся молекула столкнётся со всеми другими молекулами, центры которых находятся внутри цилиндра. Объём цилиндра за единицу времени равен πd2v. Если концентрация молекул равна n, то в единицу времени произойдёт
z = nπd2 v
столкновений, а среднее расстояние между столкновениями равно
λ = 1/n πd2 (4.20)
Строгий расчёт, проведённый Максвеллом с учётом распределения молекул по скоростям, даёт
λ = 0,71/n πd2 (4.21)
Рассмотрим две параллельные пластинки, между которыми находится газ. Одна из пластин неподвижна, а вторая двигается со скоростью u. Чтобы поддерживать эту скорость постоянной, к движущейся пластинке необходимо прикладывать силу F. Если расстояние между пластинами равно l, а площадь одной пластины – S, то, как это экспериментально установлено Ньютоном,
F = η S u/ll (4.22)
Коэффициент η в этой формуле называется коэффициентом внутреннего трения или вязкостью. Если направить ось х перпендикулярно пластинам, то формулу (4.22) можно записать так F = η S du/dх (4.23)
Как показала МКТ, вязкость газа связана с микроскопическими величинами, характеризующими движение молекул, формулой
η = 1/3 ρ v λ (4.24)
1Явление теплопроводности описывается экспериментально установленным законом Фурье. Плотность потока тепла пропорциональна в одномерном случае производной температуры по координате q = ‒ æ dТ/dх, (4.25)
где коэффициент теплопроводности æ выражается через микроскопические величины следующим образом: æ = 1/3 ρ v λ сV (4.26)
Диффузией называется проникновение молекул одного газа среди молекул другого газа. Если молекулы обоих газов мало отличаются друг от друга, то диффузию принято называть самодиффузией. Для наблюдения самодиффузии нужно как-то «пометить» часть молекул. Если Концентрация «меченых»молекул равна n1, то для одномерной самодиффузии выполняется закон Фика, диффузионный поток (количество «меченных» молекул через единичную площадку в единицу времени) пропорционален производной концентрации по координате Г1 = ‒ D dn1/dх, (4.27)
а коэффициент диффузии D = 1/3 v λ (4.28)
Расчет взаимной диффузии для газов, молекулы которых сильно отличаются друг от друга, представляет собой непростую задачу.
Тема № 5 Термодинамика
5.1 Первое начало термодинамики
В основе термодинамики лежат так называемые начала, которые являются обобщением большого числа опытов. Термодинамика, в отличии от молекулярной физики, опирается на макроскопические параметры, характеризующие термодинамическую систему в состоянии равновесия. При рассмотрении изменения состояния систем широко используются квазистатические роцессы, состоящие из непрерывно следующих друг за другом состояний равновесия.Такие процессы, строго говоря, никогда не реализуются в природе они являются физическими абстракциями. Однако многие реальные процессы, идущие с конечными скоростями, часто могут считаться приблизительно квазистатическими. В термодинамике часто используются следующие квазистатические процессы: 1) изотермический процесс, происходящий при постоянной температуре (Т = const); 2) изобарический процесс (Р = const); 3) изохорический процесс (V = const). Рассмотрим газ в цилиндре под поршнем площадью S. Если давление газа равно Р. то при перемещении поршня на расстояния dl совершается элементарная работа δА = РS dl. Поскольку изменение объёма в этом случае равно dV = S dl, то газ совершает работу
δА = Р dV (5.1)
Чтобы от элементарной работы перейти к работе для конечного процесса, надо вычислить интеграл А = ∫ Р dV
Так как давление зависит не только от объёма, но и от температуры, то работа зависит не только от начального и конечного состояния, но и от пути перехода. Про величины такого рода говорят, что они являются функциями состояния. Из геометрического смысла интеграла следует, что работа численно равна площади фигуры под графиком процесса в переменных V, Р. Важным понятием термодинамики является адиабатическая оболочка. Состояние системы, заключённой в адиабатическую оболочку, остаётся неизменным при любых изменениях температур окружающих тел, если только значения внешних параметров поддерживаются постоянными. В опытах Джоуля по определению механического эквивалента теплоты было доказано, что работа внешних сил, совершенная над системой, заключенной в адиабатическую оболочку, не зависит от пути перехода системы из начального состояния в конечное. Внутренней энергией U системы называется функция состояния, приращение которой во всяком процессе, совершаемой системой в адиабатической оболочке, равно работе внешних сил над системой при переводе её из начального состояния в конечное. Внутренняя энергия идеального одноатомного газа определяется кинетической энергией его молекул. Как следует из формулы (4.8),
U = 3/2 ν RТ (5.2)
Внутреннюю энергию системы можно изменить не только производством работы, но и путём теплообмена. Процесс обмена внутренними энергиями между телами, не сопровождающийся совершением макроскопической работы, называется теплообменом.\Энергия, переданная телу окружающей средой в результате теплообмена, называется количеством тепла. Сформулируем теперь первое начало термодинамики. Оно утверждает, что теплота Q, полученная системой, идёт на приращение её внутренней энергии и на производство внешней работы Q = ΔU + А (5.3)
Для элементарных процессов первое начало записывают в виде
δQ = dU + δА (5.4)
Такая запись подчёркивает, что только внутренняя энергия является функцией состояния. Из первого начала термодинамики следует, что невозможно совершить работу большую, чем полученная теплота, невозможно построить вечный двигатель первого рода, имеющий коэффициент полезного действия, большим единицы. Теплоёмкостью тела С называется отношение бесконечно малого количества тепла δQ, полученного телом,к соответствующему приращению dТ его температуры: С = δQ/dТ (5.5)
Особое значение имеют теплоёмкости при постоянном объёме СV и постоянном давлении СР. При постоянном объёме dV = 0 и СV = (∂U/∂Т)V (5.6)
При постоянном давлении СР = (∂Q/∂Т)Р (5.7)
Для идельного газа внутренняя энергия зависит только от температуры, поэтому
СР = СV + Р dV/dT,
Тогда СР ‒ СV = νR (5.8)
Полученная формула называется уравнением Майера. Получим уравнение адиабатического процесса. Так как δQ = 0, тодля одного моля
СV dТ + Р dV = 0 . Из уравнения Клапейрона - Менделеева
dT = (P dV + V dP)/R,
отсюда с учётом уравнения Майера
СV V dP + CP P dV = 0
Разделим полученное соотношение на СP P V и обозначим γ = СР/СV
dP/P + γ dV/V = 0
Отсюда после интегрирования и потенциирования получаем
Р Vγ = const (5.9)
Полученное соотношение называется уравнением Пуассона или уравнением адиабаты, а показатель степени при V в этом уравнении – показателем адиабаты. Рассмотрим коротко классическую теорию теплоёмкостей идеального газа. В основе этой теории лежит теорема о равномерном распределении энергии по степеням свободы. Число степеней свободы системы i равно минимальному числу независимых координат, необходимых для однозначного описания системы. По этой теореме на каждую степень свободы одной молекулы приходится энергия, равная 1/2 kТ. Тогда внутренняя энергия ν молей идеального газа равна
U = i/2 ν RT, (5.10) где число степеней свободы равно: 3 для одноатомных молекул, 5 -для двухатомных молекул и 6 – когда i ≥ 3. В этом случае
СV = i/2 νR; СР = (i + 2)/2 νR; γ = (i + 2)/i. (5.11) Например для воздуха, состоящего в основном из двухатомных молекул, показатель адиабаты при расчётах по формулам (5.11) равен 1,40, а табличное значение при нормальных условиях равно 1.41.
5.2 Второе начало термодинамики
Второе начало термодинамики позволяет судить о направлении процессов, которые могут происходить в системе. Вильям Томсон (лорд Кельвин) дал такую формулировку постулата второго начала термодинамики: «Невозможен круговой процесс, единственным результатом которого быпо бы производство работы за счёт охлаждения теплового резервуара». В такой формулировке второе начало термодинамики отрицает возможность построения вечного двигателя второго рода, имеющего коэффициент полезного действиям η = 1. Клаузиус дал существенно иную формулировку второго начала термодинамики: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому». Несмотря на кажущееся различие, обе формулировки эквивалентны. В термодинамике различают обратимые и необратимые процессы. Если в результате какого-либо процесса система перешла из состояния 1 в состояние 2 и если можно хотя бы одним способом вернуть её в состояние 1 так, чтобы во всех остальных телах не произошло никаких изменений, то процесс называется обратимым. Если же обратный процесс невозможен, переход из 1 в 2 считается необратимым. Анализируя работу тепловых машин в своей знаменитой работе «Размышления о движущей силе огня и машинах, способных развивать эту силу», Сади Карно рассмотрел работу идеальной машины, работающей по знаменитому циклу Карно. Эта машина получает от первого теплового резервуара (нагревателя) количество тепла Q1 и отдает второму резервуару (холодильнику) количество тепла Q2, совершая работу А = Q1 ‒ Q2. Карно доказал две теоремы: 1) «Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т1 и Т2 нагревателя и холодильника но не зависит ни то устройства машины, ни от вида используемого рабочего вещества»; 2) «Коэффициент полезного действия всякой тепловой машины не может превосходить к.п.д. идеальной машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника». Обе теоремы Карно можно объединить неравенством
(Q1 ‒ Q2)/Q1 ≤ (T1 ‒ T2)/T1 (5.12)
Для идеальной машины Q1//Q2 = Т1/Т2 (5.13)
В 1848 г. Вильямс Томсон (лорд Кельвин) указал, что теоремой Карно можно воспользоваться для построения температурной шкалы, совершенно не зависящей от индивидуальных особенностей термометрического вещества и устройства термометра. Для этого можно приписать какой – либо реперной точке определённое значение температуры, а температуру любого другого тела определить по формуле (5.13). Построенная таким образом шкала называется абсолютной термодинамической шкалой температур. За реперную точку такой шкалы принята тройная точка воды, ей приписано значение температуры 273,16 К точно. Из такого определения температуры следует, что она не может быть отрицательной. Из неравенства (5.12) следует интересное соотношение
Q1/Т1 ‒ Q2/Т2≤ 0 (5.14)
Клаузиус обобщил это неравенство на случай произвольного числа тепловых резервуаров. Количество тепла, отданного тепловым резервуаром, считается положительным Отношение Q/Т называется приведённым количеством тепла. Тогда для кругового процесса
∮δQ/Т ≤ 0 (5.15)
Это фундаментальное соотношение называется неравенством Клаузиуса. Если круговой процесс, совершаемый системой, - квазистатический, то неравенство Клаузиуса переходит в равенство ∮ δQ/Т = 0 (5.16) квст На этом равенстве основано введение фундаментального в термодинамике понятия энтропии. Энтропия системы есть функция её состояния, убыль которой равна приведённому количеству тепла, которое необходимо сообщить системе для её перевода из начального состояния 1 в конечное состояние 2 по любому квазистатическому путии Таким образом по определению S2 ‒ S1 = ∫ δQ/Т (5.17) 1→2 Если система переходит из состояния 1 в состояние 2 по любому пути, а возвращается назад по квазистатическому, то из неравенства Клаузиуса получаем
S2 ‒ S1 ≥ ∫ δQ/Т. 1→2 Если система адиабатически изолирована, то δQ = 0, тогда
S2 ≥ S1. (5.18)
Таким образом, энтропия адиабатически изолированной системы не может убывать. Это – закон возрастания энтропии. Наряду с энтропией, в термодинамике используются множество других, связанных с ней функций состояния. Особо важное значение имеют две функции: свободная энергия или потенциал Гельмгольца Ψ, и термодинамический потенциал или потенциал Гиббса Ф. Эти функции состояния определяются выражениями
Ψ = U ‒ Т S, (5.19)
Ф = Ψ + Р V. (5.20)
Для их дифференциалов легко получить
dΨ ≤ ‒ S dT ‒ P dV (5.21)
dФ ≤ ‒ S dT + V dP (5.22)
При изотермическом процессе dТ = 0 и dΨ ≤ ‒ δА, т.е. убыль свободной энергии при изотермическом процессе даёт максимальную работу, которую может произвести система. А убыль термодинамического потенциала даёт максимальную полезную работу, которую может произвести система.
Дальнейшие исследования в этой области привели к появлению важнейшей термодинамической функции – энтропии. Энтропия системы есть функция состояния, определённая с точностью до произвольной постоянной. Разность энтропий в двух равновесных состояниях 2 и 1, по определению, равна приведённому количеству теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути. S2 – S1 = Важную роль в природе занимает играет поверхностное натяжение на поверхности жидкости. Силы поверхностного натяжения резко возрастают при увеличении кривизны повернности жидкости. В тонких цилиндричесих капиллярах при наличии смачивания вода может подниматься вверх на высоту в десятки метров. В учении о фазах выясняются условия, при которых система, состоящая и нескольких фаз, находится в равновесии, а также анализируется влияние различных факторов на фазовые превращения.
5.3 Поверхностное натяжение
На молекулу жидкости действуют силы притяжения со стороны окружающих молекул. Если молекула находится внутри жидкости, эти силы в среднем уравновешиваются, если же она находится вблизи поверхности, то появляется результирующая сила, направленная внутрь жидкости. Поэтому для извлечения молекулы из внутренних частей жидкости на её поверхность требуется затрата работы. Величина, численно равная работе, которую необходимо совершить, чтобы изотермически и квазистатически увеличить поверхность жидкости на единицу при сохранении её объёма неизменным, называется коэффициентом поверхностного натяжения σ жидкости. Изотермическая работа, как известно, равна убыли свободной энергии системы, которую можно представить в виде суммы объёмной и поверхностной составляющих
Ψ = Ψоб + Ψпов (5.23)
Так как объём не изменяется, то σ = Ψпов/F, (5.24)
где F - площадь поверхности жидкости. Таким образом,, коэффициент поверхностного натяжения можно также определить как свободную поверхностную энергию жидкости, приходящуюся на единицу её поверхности. В состоянии равновесия свободная энергия системы должна быть минимальной, т.к. при постоянных Т и V из (5.21) следует, что dΨ ≤ 0. Поэтому в отсутствии внешних полей жидкость должна принять форму шара, т.к. из всех тел данного объёма шар имеет наименьшую поверхность, а потому и наименьшую свободную энергию. Получению шаровой формы капли мешает сила тяжести. Принцип минимума свободной поверхностной энергии в применении к растворам приводит к интересному заключению. Состав поверхностного слоя может существенно отличаться от состава основной массы жидкости. Дело в том, что различные чистые вещества имеют разные коэффициенты поверхностного натяжения, поэтому минимум свободной энергии может достигаться путём укомплектования поверхностного слоя такими молекулами, чтобы Ψ была минимальной. Вещества, адсорбирующиеся на поверхности жидкости с понижением σ, называются поверхностно-активными. Наиболее известным примером поверхностно-активного вещества является мыло. Коэффициент поверхностного натяжения жидкости уменьшается также при её нагревании. Если поместить каплю жидкости на горизонтальную поверхность, то между касательной к поверхностью жидкости и поверхностью твердого тела образуется два угла. Тот угол, который заключает в себе жидкость, называется краевым углом θ. Если краевой угол острый, то говорят, что жидкость смачивает поверхность, если θ – тупой угол, то говорят, что жидкость не смачивает поверхность. Если поверхность жидкости изогнута, то давление по разные стороны её разные. Разность давлений для астигматической поверхности определяется формулой Лапласа ΔР = σ (1/R1 + 1/R2), (5.25)
где R1и R2 радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. Если поверхность жидкости – сферическая, то (5.25) переходит в
ΔР = 2σ/R (5.26)
Внутри мыльного пузыря, оболочка которого имеет две поверхности, разность давлений ΔР = 4σ/R. (5.27) Будем считать поверхность жидкости Применим формулу Лапласа для расчёта высоты h поднятия жидкости в капилляре (от лат. Capillary – волос) радиуса r. Будем считать поверхность жидкости к капилляре сферической с радиусом кривизны R = r/cos θ, где θ – краевой угол. Тогда, приравнивая ΔР и ρgh, получаем
h = 2σ cos θ/ρgr (5.28)
Если краевой угол θ тупой, величина h отрицательна, т.е. уровень жидкости в капилляре ниже, чем в жидкости.
5.4 Фазовые превращения.
Фазой называется макроскопическая, физически однородная часть вещества, отделённая от остальных частей системы границами раздела, так что она может быть извлечена из системы механическим путём. Фаза более мелкая категория, чем агрегатное состояние вещества, - в любом агрегатном состоянии, кроме газообразного, может быть многофазная система. Важнейшим вопросом в учении о фазах является выяснение условий, при которых система, состоящая из двух или нескольких фаз, находится в равновесии. Равенство давлений и температур ещё не означает, что система находится в равновесии, необходимо ещё равновесие по отношению к взаимным превращениям фаз. Как следует из (5.22) при постоянных температурах Т и давлениях Р термодинамический потенциал может только уменьшаться, т.к. dФ ≤ 0. В состоянии равновесия значение Ф должно быть минимально. Рассмотрим систему, состоящую из двух фаз 1 и 2, которые могут превращаться друг в друга. Пусть m1 и m2 массы первой и второй фаз, а φ1 и φ2 – их удельные термодинамические потенциалы. Тогда для всей системы Ф = m1φ1 + m2φ2 (5.29)
Если φ1 > φ2, то всякое превращение фазы 1 в фазу 2 сопровождается уменьшением Ф, это превращение будет происходить, пока вся фаза 1 не перейдёт в фазу 2. Наоборот, если φ1 < φ2, то фаза 2 в конце концов превратится в фазу 1. Только при условии φ1 = φ2 возможно равновесие. Таким образом, условием равновесия фаз является равенство их удельных термодинамических потенциалов. При изменении давления температура фазового равновесия также изменяется. Приерами фазовых превращений являются изменения агрегатного состояния вещества. Найдем, например, наклон кривой испарения. При смещении вдоль кривой испарения dφ1 = dφ2, т.е. v1 dP – s1 dT = v2 dP – s2 dT, или dP/dT = (s1 – s2)/(v1 – v2) (5/30)
где v и s - удельные объём и энтропия. При переходе из газообразного состояния 1 в жидкое состояние 2 выделяется количество тепла, - удельная теплота испарения q12, поэтому
s1 – s2 = q12/Т,
тогда dP/dT = q12/(T(v1 – v2)/ (5/31)
Это важное соотношение называется уравнением Клапейрона-Клаузиуса. Для кривой испарения воды dP/dT = 36 гПа/К. Процесс интенсивного испарения, происходящий по всему объёму жидкости, называется кипением. Чтобы пузырёк, находящийся внутри жидкости на глубине h, расширялся, необходимо, чтобы давление насыщенного пара превышало сумму атмосферного, гидростатического и лапласова давления РН > РА + ρgh + 2σ/r (5.32)
При кипении жидкости, в неглубоком сосуде, если в ней имеются достаточно крупные пузырьки, вторым и третьим слагаемыми в правой части (5.32) можно пренебречь. Если число фаз химически однородного вещества равно трём, то для равновесия необходимо выполнение трёх условий: φ1 = φ2; φ2 = φ3; φ3 = φ1. Эти условия не независимы, - каждое из них является следствием двух остальных. Таким образом три фазы могут находиться в равновесии друг с другом только в одной тройной точке при вполне определённых значениях давления и температуры. Тройная точка воды используется при построении термодинамической шкалы температур
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.4 (0.012 с.) |

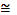 133,3 Па (4/3 гПа).
133,3 Па (4/3 гПа).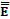 к или любую монотонную функцию её можно принять за меру температуры. попробуем суммировать наши сведения о температуре.
к или любую монотонную функцию её можно принять за меру температуры. попробуем суммировать наши сведения о температуре. к/N, (4.8)
к/N, (4.8)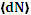 зависит от N, dω и от скорости ν, т.е.
зависит от N, dω и от скорости ν, т.е.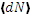 проинтегрировать по всему пространству скоростей, то, очевидно, получится полное число молекул N. Отсюда следует условие нормировки. которому должна удовлетворять функция f(v)
проинтегрировать по всему пространству скоростей, то, очевидно, получится полное число молекул N. Отсюда следует условие нормировки. которому должна удовлетворять функция f(v)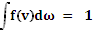 (4.12)
(4.12)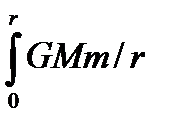 2dr = GMm/r (4.18)
2dr = GMm/r (4.18) . Энтропия адиабатически изолированной системы не может убывать; она либо возрастает, либо остаётся постоянной. Это – закон возрастании энтропии.
. Энтропия адиабатически изолированной системы не может убывать; она либо возрастает, либо остаётся постоянной. Это – закон возрастании энтропии.


