Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поле как форма материи, осуществляющая силовое взаимодействие между частицами вещества. Вес и невесомость. Потенциальная энергия тяготения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Поле как форма материи. Поля характеризуются тем, что работа, совершаемая действующими силами при перемещении м.т. из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них – Консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения м.т. из одной точки пространства в другую, то такие тела называются – Диссипативными (рассеивающими); их примером является сила трения. Вес и невесомость. Силу тяжести Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Пусть тело лежит на неподвижном относительно Земли горизонтальном столе (рис. 1.11.1). Систему отсчета, связанную с Землей, будем считать инерциальной. На тело действуют сила тяжести
Если тело неподвижно висит на пружине, то роль силы реакции опоры (подвеса) играет упругая силы пружины. По растяжению пружины можно определить вес тела и равную ему силу притяжения тела Землей. Для определения веса тела можно использовать также рычажные весы, сравнивая вес данного тела с весом гирь на равноплечем рычаге. Рассмотрим теперь случай, когда тело лежит на опоре (или подвешено на пружине) в кабине лифта, движущейся с некоторым ускорением
Сила
Пусть вектор ускорения
В этой формуле величины P, g и a следует рассматривать как проекции векторов
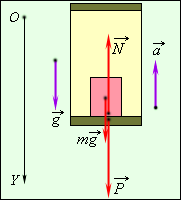
Из формулы (*) видно, что если a < g, то вес тела P в ускоренно движущемся лифте меньше силы тяжести. Если a > g, то вес тела изменяет знак. Это означает, что тело прижимается не к полу, а к потолку кабины лифта («отрицательный» вес). Наконец, если a = g, то P = 0. Тело свободно падает на Землю вместе с кабиной. Такое состояние называется невесомостью. Оно возникает, например, в кабине космического корабля при его движении по орбите при выключенными реактивных двигателями. Если вектор ускорения
Потенциальная энергия тяготения.
Применение законов сохранения к абсолютно неупругому удару. Энергия идущая на деформацию. Примеры неупругого удара. Абсолютно неупругий удар, характеризуется тем, что потенциальной энергии деформации не возникает; кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь закон сохранения импульса, закон же сохранения механической энергии не соблюдается: имеет место закон сохранения суммарной энергии различных видов — механической и внутренней. В силу закона сохранения суммарный импульс частиц после удара должен быть таким же, как и до удара:
где v - скорость движения шаров после удара. Тогда
Абсолютно неупругий удар - это пример потери механической энергии под действием диссипативных сил.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни.
с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни. направленная вертикально вниз, и сила упругости
направленная вертикально вниз, и сила упругости  с которой опора действует на тело. Силу
с которой опора действует на тело. Силу  называют силой нормального давления или силой реакции опоры. Силы, действующие на тело, уравновешивают друг друга:
называют силой нормального давления или силой реакции опоры. Силы, действующие на тело, уравновешивают друг друга: 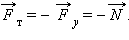 В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой
В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой 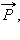 равной по модулю силе реакции опоры и направленной в противоположную сторону:
равной по модулю силе реакции опоры и направленной в противоположную сторону:  По определению, сила
По определению, сила  и называется весом тела. Из приведенных выше соотношений видно, что
и называется весом тела. Из приведенных выше соотношений видно, что  т. е. вес тела
т. е. вес тела  Но эти силы приложены к разным телам!
Но эти силы приложены к разным телам!
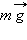 – сила тяжести,
– сила тяжести, 
 относительно Земли. Система отсчета, связанная с лифтом, не является инерциальной. На тело по-прежнему действуют сила тяжести
относительно Земли. Система отсчета, связанная с лифтом, не является инерциальной. На тело по-прежнему действуют сила тяжести 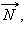 но теперь эти силы не уравновешивают друг друга. По второму закону Ньютона
но теперь эти силы не уравновешивают друг друга. По второму закону Ньютона
 Следовательно, вес тела в ускоренно движущемся лифте есть
Следовательно, вес тела в ускоренно движущемся лифте есть
 направлен по вертикали (вниз или вверх). Если координатную ось OY направить вертикально вниз, то векторное уравнение для
направлен по вертикали (вниз или вверх). Если координатную ось OY направить вертикально вниз, то векторное уравнение для  и
и 
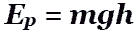 Потенциальная энергия тяготения не зависит от формы трактории, а зависит от его высоты относительно нулевого уровня.
Потенциальная энергия тяготения не зависит от формы трактории, а зависит от его высоты относительно нулевого уровня.  - работа силы тяжести и изменение потенциальной энергии тяготения.
- работа силы тяжести и изменение потенциальной энергии тяготения.

 (15.10)
(15.10)