
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 9. Реальные газы и жидкости. (4 ч.)Содержание книги
Поиск на нашем сайте
Отклонение поведения реальных газов от законов идеального газа. Силы межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса. Физический смысл постоянных в уравнении Ван-дер-Ваальса Изотермы Ван-дер-Ваальса. Критическая точка. Внутренняя энергия реального газа. Фазовые переходы 1 и 2 рода. Фазовые диаграммы. Тройная точка. Уравнение Клапейрона-Клаузиуса. Плавление и кристаллизация. Аморфные тела. Испарение и конденсация.
Вопросы для самопроверки: 1. Каковы границы применимости модели идеального газа? 2. Расскажите о силах межмолекулярного взаимодействия. 3. Запишите уравнение состояния реального газа Ван-дер-Ваальса. 4. Чем отличаются реальные газы от идеальных? Каков смысл поправок при выводе уравнения Ван-дер-Ваальса? 5. Почему перегретая жидкость и пересыщенный пар являются метастабильными состояниями? 6. Почему у всех веществ поверхностное натяжение уменьшается с температурой? Что представляют собой поверхностно-активные вещества? 7. При каком условии жидкость смачивает твердое тело? не смачивает? От чего зависит высота поднятия смачивающей жидкости в капилляре? 8. Чем отличаются монокристаллы от поликристаллов? Как можно классифицировать кристаллы? Какие тела называют аморфными? 9. Что называют фазовым переходом? 10. Чем отличается фазовый переход I рода от фазового перехода II рола? 11. Что можно «вычитать» из диаграммы состояния, используемой для изображения фазовых превращений? 12. Запишите уравнение Клапейрона-Клаузиуса.
Задачи для решения на занятии: 1. В баллоне вместимостью V= 8л находится кислород массой m =0,3кг при температуре T =300К. Найти, какую часть вместимости сосуда составляет собственный объем молекул газа. Определить отношение внутреннего давления р' к давлению р газа на стенки сосуда. 2. Углекислый газ, содержащий количество вещества v =lмоль находится в критическом состоянии. При изобарном нагревании газа его объем V увеличился в k=2 раза. Определить изменение DТ температуры газа, если его критическая температура Ткр =304К. 3. В цилиндре под поршнем находится хлор массой m =20г. Определить изменение DU внутренней энергии хлора при изотермическом расширении его от V1 =200см3 до V2 =500см3. 4. Найти добавочное давление р внутри мыльного пузыря диаметром d= 10см. Определить также работу А, которую нужно совершить, чтобы выдуть этот пузырь. 5. Определять изменение свободной энергии DЕ поверхности мыльного пузыря при изотермическом увеличении его объема от V1 =10cм3 дo V2=2V1. 6. В сосуде с глицерином падает свинцовый шарик. Определить максимальное значение диаметра шарика, при котором движение слоев глицерина, вызванное падением шарика, является еще ламинарным. Движение считать установившимся. 7. Трубка имеет диаметр d1 =0,2 см. На нижнем конце трубки повисла капля воды, имеющая в момент отрыва вид шарика. Найти диаметр d2 этой капли. 8. На какую высоту h поднимается вода между двумя параллельными друг другу стеклянными пластинками, если расстояние d между ними равно 0,2мм? 9. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость v1 воды в широкой части трубы равна 20см/с. Определить скорость v2 в узкой части трубы, диаметр d2 которой в 1,5 раза меньше диаметра d1 широкой части. 10. Медный шарик диаметром d =1см падает с постоянной скоростью в касторовом масле. Является ли движение масла, вызванное падением в нем шарика, ламинарным? Критическое значение числа Рейнольдса Reкр =0,5.
Домашнее задание: 1. В сосуде вместимостью V= 10л находится азот массой m =0,25кг. Определить: 1) внутреннее давление р' газа: 2) собственный объем V ¢ молекул. 2. Определить давление р, которое будет производить кислород, содержащий количество вещества n=lмоль, если он занимает объём V =0,5л при температуре T =300К. Сравнить полученный результат с давлением, вычисленным по уравнению Менделеева — Клапейрона. 3. В сосуде вместимостью V =0,3л находится углекислый газ, содержащий количество вещества n=lмоль при температуре Т =300К. Определить давление р газа: 1) по уравнению Менделеева — Клапейрона; 2) по уравнению Ван-дер-Ваальса. 4. Определить внутреннюю энергию U азота, содержащего количество вещества n=lмоль, при критической температуре Ткр =126К. Вычисления выполнить для четырех значений объемов V: 1) 20л; 2) 2л; 3) 0,2л; 4) Vкр. 5. Найти внутреннюю энергию U углекислого газа массой m =132г при нормальном давлении p0 и температуре T ==300К в двух случаях, когда газ рассматривают: 1) как идеальный; 2) как реальный. 6. Масса m 100 капель спирта, вытекающего из капилляра, равна 0,71г. Определить поверхностное натяжение s спирта, если диаметр d шейки капли в момент отрыва равен 1мм. 7. На сколько давление р воздуха внутри мыльного пузыря больше атмосферного давления ро, если диаметр пузыря d= 5см? 8. В широкой части горизонтально расположенной трубы нефть течет со скоростью v1 =2 м/с. Определить скорость v2 нефти в узкой части трубы, если разность Dр давлений в широкой и узкой частях ее равна 6,65кПа. 9. Латунный шарик диаметром d =0,6 мм падает в глицерине. Определить: 1) скорость v установившегося движения шарика; 2) является ли при этой скорости обтекание шарика ламинарным? 10. При движении шарика радиусом r1 =2,4мм в касторовом масле ламинарное обтекание наблюдается при скорости v1 шарика, не превышающей 10см/с. При какой минимальной скорости v2 шарика радиусом r2 =1мм в глицерине обтекание станет турбулентным?
Тема 11. Контрольная работа №2. (2 ч.) Вопросы для коллоквиума 1. 1. Молекулярная физика и термодинамика. Предмет и методы. Основные параметры состояния системы. 2. Газовые законы (Бойля-Мариотта, Гей-Люссака, Шарля, Авогадро, Дальтона). 3. Уравнение состояния идеального газа Клапейрона-Менделеева. 4. Основное уравнение МКТ. 5. Распределение молекул идеального газа по скоростям (Максвелла). 6. Барометрическая формула, распределение Больцмана. 7. Явления переноса; диффузия, теплопроводность, вязкость. 8. Средняя длина свободного пробега и среднее число столкновений молекул. 9. Внутренняя энергия идеального газа, число степеней свободы молекул. 10. Первое начало термодинамики, теплоемкость (виды, определения, связь). 11. Молярная теплоемкость идеального газа при постоянном объёме и при постоянном давлении. 12. Адиабатический и политропный процессы. 13. Круговые процессы (циклы), КПД. 14. Энтропия. Второе начало термодинамики. 15. Реальные газы, уравнение состояния. 16. Реальные газы, изотермы Ван-дер-Ваальса. 17. Жидкости и их свойства: поверхностное натяжение. 18. Жидкости и их свойства: смачивание. 19. Давление под искривленной поверхностью жидкости. 20. Капиллярные явления. 21. Твердые тела: типы и виды кристаллов. 22. Плавление, кристаллизация, сублимация твердых тел, аморфные тела. 23. Фазовые переходы I и II рода. 24. Диаграмма состояний, тройная точка.
Вопросы для самостоятельной контролируемой работы студентов 1. Температура и термодинамическое равновесие. Температурные шкалы. 2. Способы измерения температуры и виды термометров. 3. Экспериментальное обоснование молекулярно-кинетической теории: основные экспериментальные факты о строении вещества, межмолекулярных взаимодействиях, тепловом движении. 4. Экспериментальное определение средней длины свободного пробега и скорости молекул. 5. Явления в разреженных газах: внутреннее трение и теплопроводность. 6. Методы получения низких температур и сжижение газов. 7. Испарение и кипение жидкостей. Насыщенный пар. Точка росы. III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ. Основные законы и формулы.
Электричество · Закон Кулона:
· Закон сохранения зарядов. В любой замкнутой системе заряженных
где n — число заряженных тел в системе. · Напряженность Е электрического поля:
· Сила, действующая на точечный заряд q, помещенный в электрическое поле, выражается формулой
· Поток вектора напряженности электрического поля
· Теорема Остроградского — Гаусса. Поток Ф Е вектора напряженности Е через любую замкнутую поверхность, охватывающую заряды q1, q2,.... qn:
где qi — заряд, заключенный внутри поверхности (со своим знаком), n — число зарядов. · Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда, выражается формулой:
· Напряженность электрического поля, создаваемого металлической заряженной сферой радиуса R на расстоянии r от центра сферы: а) внутри сферы (r < R)
б) на поверхности сферы (r = R)
в) вне сферы (r > R)
где q — заряд сферы. · Принцип суперпозиции: напряженность Е результирующего поля равна векторной (геометрической) сумме напряженностей складываемых полей:
· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси,
где Линейная плотность заряда есть физическая величина, численно равная заряду, приходящемуся на единицу длины нити (цилиндра):
· Напряженность поля, создаваемого бесконечной равномерно
где Поверхностная плотность заряда есть физическая величина, численно равная заряду, приходящемуся на единицу площади:
· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по абсолютной величине поверхностной плотностью заряда (поле плоского конденсатора)
· Сила притяжения пластин плоского конденсатора
· Индукция D электрического поля связана с напряженностью Е электрического поля соотношением
· Потенциал
· Потенциал
· Потенциал электрического поля, создаваемого металлической заряженной сферой радиуса R на расстоянии r от центра сферы: а) внутри сферы (r<R)
б) на поверхности сферы (r=R)
в) вне сферы (r>R)
где q - заряд сферы. · Если электрическое поле создано системой п точечных зарядов, то потенциал его
· Энергия W системы точечных зарядов
где · Потенциал связан с напряженностью электрического поля соотношениями: a) в общем случае
б) в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по величине, так и по направлению,
где d — расстояние между этими эквипотенциальными поверхностями, взятое вдоль электрической силовой линии. · Электроемкость уединенного проводника
· Электроемкость С уединенной металлической сферы радиуса R, находящейся в бесконечной среде с диэлектрической проницаемостью
· Электроемкость С плоского конденсатора, площадь пластин (каждой пластины) которого S, а расстояние между ними d:
где · Электроемкость сферического конденсатора
· Электроемкость цилиндрического конденсатора
· Электроемкость С последовательно соединенных двухконденсаторов
· Электроемкость двух параллельно соединенных конденсаторов
· Энергия заряженного конденсатора:
· Сила постоянного тока I есть скалярная физическая величина, численно равная количеству электричества, прошедшему через поперечное сечение проводника в единицу времени:
где q — количество электричества, прошедшее через поперечное сечение проводника за время t. · Закон Ома для участка цепи,
Сопротивление R однородного проводника длиной l и одинаковой по всей длине площадью поперечного сечения S вычисляется по формуле
где · Зависимость удельного сопротивления проводника от температуры выражается соотношением
· Закон Ома для полной цепи
· Закон Ома для участка цепи, содержащего э. д. с.
· Законы Кирхгофа 1. Алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
2. В любом замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме э. д. с., имеющихся в этом контуре:
· Мощность тока
· Закон Джоуля — Ленца. Работа электрического тока (тепловое действие тока)
Магнетизм · Закон Био-Савара-Лапласа.
или
где · Магнитная индукция В связана с напряженностью Н магнитного поля соотношением
или в вакууме
· Магнитная индукция в центре кругового проводника с током:
· Магнитная индукция поля, создаваемая бесконечно длинным прямым проводником с током:
Магнитная индукция поля, создаваемого отрезком проводника:
· Магнитная индукция поля, создаваемая соленоидом в средней его части
где n - число витков, приходящихся на единицу длины соленоида, J - сила тока в одном витке. · Принцип суперпозиции магнитных полей
· Закон Ампера.
или
· Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами I1 и I2, находящихся на расстоянии d друг от друга, рассчитанная на отрезок проводника длиной l, выражается формулой:
· Механический момент, действующий на контур с током, помещенный в однородное магнитное поле, или
где pm — магнитный момент контура с током, равный произведению силы тока J в контуре на площадь S, охватываемую этим контуром,
· Cила Лоренца
или
· Работа перемещения замкнутого контура с током в магнитном поле определяется соотношением
· Основной закон электромагнитной индукции
· Разность потенциалов U на концах проводника длиной l, движущегося в однородном магнитном поле со скоростью ν, выражается формулой
где · Электродвижущая сила индукции
где · Электродвижущая сила самоиндукции
где L — индуктивность (коэффициент самоиндукции) контура. · Индуктивность L соленоида (тороида) пропорциональна квадрату числа витков п на единицу длины соленоида и объему V соленоида
· Энергия W магнитного поля, создаваемого соленоидом с индукцией L, определяется формулой
где J — сила тока в соленоиде.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.128.17 (0.008 с.) |

 ,
, .
. = 9·109м/Ф.
= 9·109м/Ф. ,
, .
.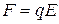 .
. .
. ,
, .
.
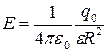

 ,
,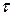 — линейная плотность заряда.
— линейная плотность заряда. .
. ,
, — поверхностная плотность заряда.
— поверхностная плотность заряда.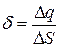
 .
. ,
, ,
,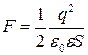 .
. .
. электрического поля
электрического поля
 .
. электрического поля, создаваемый точечным зарядом q на расстоянии r от заряда, выражается формулой
электрического поля, создаваемый точечным зарядом q на расстоянии r от заряда, выражается формулой .
.
 ,
, .
. выражается формулой
выражается формулой ,
, — потенциал поля, создаваемого всеми n -1 зарядами (за исключением 1-го) в точке, где расположен заряд
— потенциал поля, создаваемого всеми n -1 зарядами (за исключением 1-го) в точке, где расположен заряд  .
.
 ,
, и
и  — потенциалы точек двух эквипотенциальных поверхностей,
— потенциалы точек двух эквипотенциальных поверхностей, .
. :
: .
. ,
, .
. .
. .
. .
. ,
, ,
,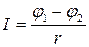 .
. ,
, — удельное сопротивление проводника.
— удельное сопротивление проводника. ,
, .
. .
. .
. .
. .
. .
.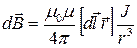
 ,
, — магнитная постоянная,
— магнитная постоянная, 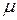 — магнитная проницаемость среды (для вакуума
— магнитная проницаемость среды (для вакуума 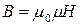
 .
. .
. .
. .
. ,
, .
.
 .
. .
.
 ,
, .
.
 ,
, ,
, ,
, ,
, - угол между направлением вектора скорости v и вектора магнитной индукции В.
- угол между направлением вектора скорости v и вектора магнитной индукции В. , возникающая в рамке, содержащей N витков площадью S, при вращении рамки с угловой скоростью
, возникающая в рамке, содержащей N витков площадью S, при вращении рамки с угловой скоростью  в однородном магнитном поле с индукцией В определяется уравнением
в однородном магнитном поле с индукцией В определяется уравнением ,
, — мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки.
— мгновенное значение угла между вектором В и вектором нормали n к плоскости рамки.
 ,
, .
. ,
,


