
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие максимумов интенсивности светаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
где φ' — приближенное значение угла дифракции. · Дифракция света на дифракционной решетке при нормальном падении лучей. Условие главных максимумов интенсивности
где d — период (постоянная) решетки; k — номер главного максимума; φ —угол между нормалью к поверхности решетки и направлением дифрагированных волн. · Разрешающая сила дифракционной решетки
где Δ λ — наименьшая разность длин волн двух соседних спектральных линий (λ и λ +Δ λ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N — число штрихов решетки; k — порядковый номер дифракционного максимума. · Угловая дисперсия дифракционной решетки
линейная дисперсия дифракционной решетки
Для малых углов дифракции
где f — главное фокусное расстояние линзы, собирающей на экране дифрагирующие волны.
Поляризация света · Закон Брюстера
где · Закон Малюса
где I — интенсивность плоскополяризованного света, прошедшего через анализатор; I0 — интенсивность плоскополяризованного света, падающего на анализатор; · Степень поляризации света
где I max и I min — максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором. · Угол поворота φ плоскости поляризации оптически активными веществами определяется соотношениями: а) в твердых телах б) в чистых жидкостях в) в растворах
Законы теплового излучения · Закон Стефана — Больцмана
где [ s = 5,67∙10-8 Вт/(м2∙К4)]. · Энергетическая светимость серого тела
где ε — коэффициент теплового излучения (степень черноты) серого тела. · Закон смещения Вина
где λm — длина волны, на которую приходится максимум энергии излучения; b— постоянная закона смещения Вина (b =2,90×10-3 м*К). · Формула Планка
где
Фотоэлектрический эффект. · Формула Эйнштейна: а) в общем случае
где б) в случае, если энергия фотона много больше работы выхода (
Максимальная кинетическая энергия фотоэлектрона в двух случаях (нерелятивистском и релятивистском) выражается различными формулами: а) если фотоэффект вызван фотоном, имеющим незначительную энергию (
где m 0 — масса покоя электрона; б) если фотоэффект вызван фотоном, обладающим большой энергией (
где · Красная граница фотоэффекта
где λ 0 — максимальная длина волны излучений ( Давление света, фотоны. · Давление, производимое светом при нормальном падении,
где Ee — облученность поверхности; с — скорость электромагнитного излучения в вакууме; w — объемная плотность энергии излучения; ρ — коэффициент отражения. · Энергия фотона
где h — постоянная Планка; · Масса и импульс фотона выражаются соответственно формулами
Радиоактивность. · Основной закон радиоактивного распада
где N — число нераспавшихся атомов в момент времени t; N 0 — число нераспавшихся атомов в момент, принятый за начальный (при t=0); е — основание натуральных логарифмов; λ — постоянная радиоактивного распада. · Период полураспада T 1/2 — промежуток времени, за который число нераспавшихся атомов уменьшается в два раза. Период полураспада связан с постоянной распада соотношением
· Число атомов, распавшихся за время t,
Если промежуток времени ∆t << T 1/2, то для определения числа распавшихся атомов можно применять приближенную формулу
Среднее время жизни
· Число атомов, содержащихся в радиоактивном изотопе,
где m — масса изотопа; М — его молярная масса; N A — постоянная Авогадро. · Активность А нуклида в радиоактивном источнике (активность изотопа) есть величина, равная отношению числа dN ядер, распавшихся в изотопе, к промежутку времени dt, за которое произошел распад. Активность определяется по формуле
или после замены N по основному закону радиоактивного распада
Активность изотопа в начальный момент времени (t=0)
Активность изотопа изменяется со временем по тому же закону, что и число нераспавшихся ядер:
· Массовая активность а радиоактивного источника есть величина, равная отношению его активности A к массе т этого источника, т. е.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1344; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.006 с.) |

 ,
,  ,
, ,
,  ,
, ,
,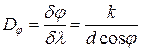 ,
, .
. ,
,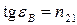 ,
,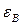 — угол падения, при котором отраженная световая волна полностью поляризована; n 21 — относительный показатель преломления.
— угол падения, при котором отраженная световая волна полностью поляризована; n 21 — относительный показатель преломления. ,
, — угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора.
— угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора. ,
, , где
, где  , где
, где  — удельное вращение; ρ — плотность жидкости;
— удельное вращение; ρ — плотность жидкости; , где С — массовая концентрация оптически активного вещества в растворе.
, где С — массовая концентрация оптически активного вещества в растворе. ,
, — энергетическая светимость черного тела; Т — термодинамическая температура; s — постоянная Стефана — Больцмана
— энергетическая светимость черного тела; Т — термодинамическая температура; s — постоянная Стефана — Больцмана
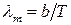 λm,
λm,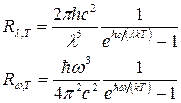
 ,
, 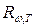 — спектральные плотности энергетической светимости черного тела; λ — длина волны; w — круговая частота; с— скорость света в вакууме; k — постоянная Больцмана; Т — термодинамическая температура; h— постоянная Планка; ħ=h/(2π) - постоянная Планка, деленная на 2π.
— спектральные плотности энергетической светимости черного тела; λ — длина волны; w — круговая частота; с— скорость света в вакууме; k — постоянная Больцмана; Т — термодинамическая температура; h— постоянная Планка; ħ=h/(2π) - постоянная Планка, деленная на 2π. , или
, или  ,
,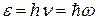 — энергия фотона, падающего на поверхность металла; А — работа выхода электрона из металла; T max — максимальная кинетическая энергия фотоэлектрона;
— энергия фотона, падающего на поверхность металла; А — работа выхода электрона из металла; T max — максимальная кинетическая энергия фотоэлектрона; ),
),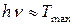 , или
, или 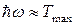 .
.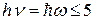 кэВ), то
кэВ), то ,
,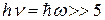 кэВ), то
кэВ), то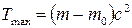 или
или 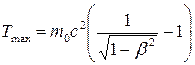 ,
,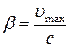 — масса релятивистского электрона.
— масса релятивистского электрона.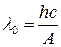 ,
, 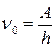 или
или  ,
, и
и 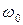 — минимальные соответственно частота и круговая частота), при которых еще возможен фотоэффект.
— минимальные соответственно частота и круговая частота), при которых еще возможен фотоэффект.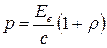 или
или 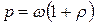 ,
,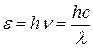 или
или  ,
, ;
; 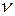 - частота света;
- частота света;  — круговая частота; λ — длина волны.
— круговая частота; λ — длина волны. ;
;  .
.
 .
.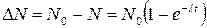 .
.
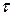 радиоактивного ядра — промежуток времени, за который число нераспавшихся ядер уменьшается в е раз:
радиоактивного ядра — промежуток времени, за который число нераспавшихся ядер уменьшается в е раз: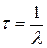
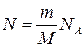
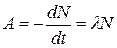 ,
,
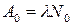 .
.
 .
.


