
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика материальной точки и тела,Содержание книги
Поиск на нашем сайте
ФИЗИКА УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
Ставрополь
Печатается по решению редакционно-издательского совета Ставропольского государственного университета
Физика: Учебно-методическое пособие. – Ставрополь: Изд-во СГУ, 2010. – 160 с.
Учебно-методическое пособие разработано в соответствии с Государственным образовательным стандартом высшего профессионального образования для специальности 060112 – «Медицинская биохимия», включает основные теоретические сведения, вопросы для самопроверки, задачи для решения в аудитории, домашние задания, вопросы для самостоятельной контролируемой работы, вопросы для коллоквиумов и экзаменов, примерные темы рефератов. Предназначено для студентов 2-3 курса специальности «Медицинская биохимия».
Авторы-составители: канд. физ.-мат. наук Беджанян М.А. канд. физ.-мат. наук Нечаева О.А.
Рецензент: кандидат физико-математических наук, доцент Копылова О.С. © Издательство Ставропольского государственного университета, 2010 Пояснительная записка ФИЗИКА – по-гречески – ПРИРОДА, это наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы ее движения. В системе подготовки специалистов по специальности 040800 – «Медицинская биохимия» Государственного образовательного стандарта высшего профессионального образования курс физики занимает значительное место. Физика изучается в 3 – 6 семестрах и является основой для изучения других предметов естественнонаучного цикла. Основными целями изучения курса являются: - освоение основных законов и положений физики; - развитие у студентов физического мышления, чтобы будущий специалист мог не только самостоятельно решать различные физические проблемы, но и перенести общие методы научной работы в работу по специальности; - овладение экспериментальными навыками и умениями и их развитие; - формирование и развитие интеллектуальных и творческих способностей, навыков самостоятельной работы при решении физических задач и научных исследованиях; - формирование физической картины мира; - воспитание трудолюбия и настойчивости в достижении поставленной цели, понимания необходимости разумного использования достижений современной науки, отношения к физике как элементу общечеловеческой культуры; Важнейшие задачи обучения курса физики – это сообщение знаний и развитие умений решать задачи, а также вести самостоятельно экспериментальную работу и проводить анализ результатов, наблюдений и экспериментов. В результате изучения дисциплины студент должен: иметь представление: - о Вселенной в целом как физическом объекте и ее эволюции; - о фундаментальном единстве естественных наук, незавершенности и возможности его дальнейшего развития; - о дискретности и непрерывности в природе; - о соотношении порядка и беспорядка в природе, упорядоченности строения объектов, переходах в неупорядоченное состояние и наоборот; - о динамических и статистических закономерностях в природе; - о вероятности как объективной характеристике природных систем; - об измерениях и их специфичности в различных разделах естествознания; - о фундаментальных константах естествознания; - о принципах симметрии и законах сохранения; - о соотношениях эмпирического и теоретического в познании; - о состояниях в природе и их изменениях со временем; - об индивидуальном и коллективном поведении объектов в природе; - о времени в естествознании; - о физическом моделировании. уметь: - использовать основные законы физики и активно применять эти знания для анализа физико-химической сущности явлений; - строить физические модели и решать конкретные задачи заданной степени сложности; - планировать, осуществлять и анализировать научный эксперимент, а также оценивать точность полученных результатов; - самостоятельно работать с литературой. Владеть методами теоретического и экспериментального исследования в физике. Иметь опыт (навык) решения прикладных задач. Физика имеет междисциплинарные связи со следующими дисциплинами: биофизика, математические дисциплины, биология, химия, концепции современного естествознания. В процессе преподавания физики на специальности 060112 – «Медицинская биохимия» используются такие традиционные виды занятий, как лекции, практические и лабораторные занятия. Чтение лекций сопровождается презентациями, подготовленными с помощью программы Power Point. Самостоятельная работа студентов предполагает: предварительную подготовку к занятиям, подбор, изучение, анализ и конспектирование рекомендованной литературы по физике, выполнение специальных учебных заданий, написание контрольных, участие в научных исследованиях, проводимых на кафедре, в университете, подготовка рефератов, презентаций, участие в студенческих олимпиадах и другие. I. МЕХАНИКА Основные законы и формулы. Кинематика. · Положение материальной точки в пространстве задается радиус-вектором r:
где Кинематические уравнения движения в координатной форме:
где t – время. · Средняя скорость
где Средняя путевая скорость
где Мгновенная скорость
где Модуль скорости
· Ускорение
где Модуль ускорения
Модули этих ускорений
где R – радиус кривизны в данной точке траектории · Кинематическое уравнение равномерного движения материальной точки вдоль оси х
где х0 - начальная координата;
· Кинематическое уравнение равнопеременного движения (
где Скорость точки при равнопеременном движении
· Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) Кинематическое уравнение вращательного движения
· Средняя угловая скорость
где ∆ Мгновенная угловая скорость
· Угловое ускорение
· Кинематическое уравнение равномерного вращения
где При равномерном движении
Частота вращения
где N – число оборотов, совершаемых телом за время · Кинематическое уравнение равнопеременного вращения (
где Угловая скорость тела при равнопеременном вращении
· Связь между линейными и угловыми величинами, характеризующие вращение материальной точки, выражается следующими формулами: путь, пройденный точкой по дуге окружности радиусом R,
скорость точки линейная
ускорение точки: тангенциальное
нормальное:
Движущегося поступательно. · Уравнение движения материальной точки (второй закон Ньютона): в векторной форме
где в координатной форме (скалярной):
или
где под знаком суммы стоят проекции сил · Сила упругости
где k – коэффициент упругости (жесткость в случае пружины); x – абсолютная деформация. · Сила гравитационного взаимодействия
где G – гравитационная постоянная; т1 и т2 – массывзаимодействующих тел, рассматриваемых как материальные точки; r – расстояние между ними. 4. Сила трения скольжения
где f – Коэффициент трения скольжения; N – сила нормального давления. · Координаты центра масс материальных точек
где mi – масса i -той материальной точки; · Закон сохранения импульса
где N – число материальных точек (или тел), входящих в систему. · Работа, совершаемая постоянной силой
где · Работа, совершаемая постоянной силой
где интегрирование ведется вдоль траектории, обозначаемой L. · Средняя мощность за интервал времени
· Мгновенная мощность
где dA – работа, совершаемая за промежуток времени · Кинетическая энергия материальной точки (или тела, движущегося поступательно)
· Потенциальная энергия тела и сила, действующая на тело в данной точке поля, связаны соотношением
где
· Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины)
· Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами т1 и т2, находящихся на расстоянии r друг от друга,
· Потенциальная энергия тела, находящегося в однородном поле силы тяжести
где h – высота тела над уровнем, принятым за нулевой для отсчета потенциальной энергии. Эта формула справедлива при условии h<<R, где R – радиус Земли. · Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде
· Применяя законы сохранения энергии и импульса к прямому центральному удару шаров, получаем формулу скорости абсолютно неупругих шаров после удара:
и формулу скорости абсолютно упругих шаров после удара:
где т1 и т2 - массы шаров; v1 и v2 – их скорости до удара.
Механика жидкостей и газов. · Расход жидкости в трубке тока:
а) объемный расход (объем жидкости, протекающей через сечение
б) массовый расход (масса жидкости, протекающей в единицу времени
где S — площадь поперечного сечения трубки тока, v — скорость жидкости, р — плотность жидкости. · Уравнение неразрывности струи
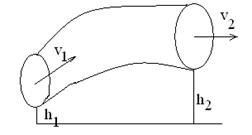
где S1 и S2 — площади поперечного сечения трубки тока в двух местах, v1 и v2 — соответствующие скорости течений. · Уравнение Бернулли: а) в общем случае
где р1 и р2 — статические давления жидкости в двух сечениях трубки тока, ν1 и v2 — скорости течения жидкости в этих сечениях, б) в случае когда оба сечения находятся на одной высоте (h1=h2):
· Скорость истечения жидкости из малого отверстия в открытом широком сосуде:
где h — глубина, на которой находится отверстие относительно уровня жидкости в сосуде. · Сила сопротивления, испытываемая шариком при падении в вязкой жидкости (формула Стокса),
где · Объем жидкости (газа), протекающей за время t через длинную трубку (формула Пуазейля),
где r— радиус трубки, l — длина трубки, · Число Рейнольдса: а) для потока жидкости в длинных трубках
где б) для движения шарика в жидкости
где ν — скорость движения шарика, d — его диаметр.
Вопросы для коллоквиума 1. 1. Предмет физики. Связь физики с другими науками. 2. Механическое движение и его виды. 3. Система отсчета. Траектория, путь, перемещение. 4. Скорость (определение, виды, направление, единицы измерения). 5. Ускорение (определение, виды, направление, единицы измерения). 6. Движение по окружности: угловой путь, угловая скорость, угловое ускорение. 7. Связь линейных и угловых величин. 8. Законы Ньютона. Масса и сила. Импульс. 9. Закон всемирного тяготения. 10. Сила тяжести, вес тела. Ускорение свободного падения. 11. Силы упругости. 12. Трение и его виды. 13. Силы инерции. 14. Момент инерции. Моменты инерции некоторых тел. 15. Теорема Штейнера. 16. Момент силы. Основной закон динамики вращения. 17. Момент импульса. 18. Работа и мощность. Энергия.
Вопросы для коллоквиума 2. 1. Кинетическая механическая энергия. 2. Потенциальная механическая энергия. 3. Полная механическая энергия. 4. Кинетическая энергия вращающегося тела, катящегося тела. 5. Закон сохранения импульса. 6. Закон сохранения момента импульса. 7. Закон сохранения и превращения энергии. 8. Механические колебания (свободные, гармонические, затухающие, вынужденные) и их уравнения. 9. Маятники (математический, физический, пружинный) 10. Сложение одинаково направленных гармонических колебаний. 11. Сложение взаимно перпендикулярных гармонических колебаний. 12. Затухающие и вынужденные колебания, резонанс. 13. Волны, механические волны, уравнение бегущей волны, основные характеристики волн. 14. Интерференция волны. Стоячие волны. 15. Эффект Доплера. Звук и его восприятие. 16. Противоречия классической механики. Создание СТО. 17. Принцип относительности и постулат скорости света. Пространство и время в теории относительности. Преобразования Лоренца. 18. Следствия из преобразований Лоренца. Относительность одновременности и причинность. Сокращение длины двигающихся отрезков и замедление темпа хода двигающихся часов. 19. Сложение скоростей. Релятивистское уравнение движения. 20. Импульс и скорость. Соотношение между массой и энергией. 21. Давление в жидкости и газе. 22. Ламинарное, турбулентное течение. 23. Уравнение Бернулли, уравнение неразрывности. 24. Движение тел в жидкостях и газах, вязкость.
Вопросы для самостоятельной контролируемой работы студентов 1. Неинерциальные системы отсчета. 2. Свободные оси. Гироскоп. 3. Законы Кеплера. 4. Космические скорости. 5. Реактивное движение. 6. Механические свойства биологических тканей. 7. Движение тел в газах. 8. Физическая модель сосудистой системы. 9. Физические основы устройства аппарата речи и слуха человека. 10. Ударные волны. 11. Ультра- и инфразвук в природе и технике.
Основные законы и формулы.
· Количество вещества где N — число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); NA — постоянная Авогадро: NA =6,02×1023 моль-1. · Молярная масса вещества
где m — масса однородного тела (системы); v — количество вещества этого тела. · Относительная молекулярная масса вещества
где ni — число атомов i -го химического элемента, входящего в состав молекулы данного вещества; A r, i — относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева. · Связь молярной массы М с относительной молекулярной массой M r вещества
где k =10-3 кг/моль. · Молярная масса смеси газов
где mi — масса i -го компонента смеси; vi — количество вещества 1-го компонента смеси; k — число компонентов смеси. · Уравнение состояния идеальных газов (уравнение Клапейрона — Менделеева)
где m — масса газа; М — его молярная масса; R — молярная газовая постоянная; Т — термодинамическая температура; v — количество вещества. · Закон Дальтона где p — давление смеси газов; pi — парциальное давление i -го компонента смеси; k — число компонентов смеси. · Концентрация частиц (молекул, атомов и т. п.) однородной системы
где V — объем системы. · Основное уравнение кинетической теории газов
где р — давление газа; · Средняя кинетическая энергия: приходящаяся на одну степень свободы молекулы
· Зависимость давления газа от концентрации молекул и температуры
· Скорость молекул: средняя квадратичная
средняя арифметическая
наиболее вероятная
где m1 — масса одной молекулы. · Распределение Больцмана (распределение частиц в силовом поле) где п — концентрация частиц; U — их потенциальная энергия; n 0 — концентрация частиц в точках поля, где U =0; k — постоянная Больцмана; T — термодинамическая температура; е — основание натуральных логарифмов. · Барометрическая формула (распределение давления в однородном поле силы тяжести)
где р — давление газа; m — масса частицы; М — молярная масса; z — координата (высота) точки по отношению к уровню, принятому за нулевой; р 0 — давление на этом уровне; g — ускорение свободного падения; R — молярная газовая постоянная. · Среднее число соударений, испытываемых одной молекулой газа в единицу времени,
где d — эффективный диаметр молекулы; п — концентрация молекул; <J> — средняя арифметическая скорость молекул. · Средняя длина свободного пробега молекул газа
· Динамическая вязкость
где r — плотность газа (жидкости); <J> — средняя скорость хаотического движения его молекул; < l > — их средняя длина свободного пробега. · Закон Ньютона
где F — сила внутреннего трения между движущимися слоями газа. · Закон Фурье
где DQ — теплота, прошедшая посредством теплопроводности через сечение площадью S за время Dt; l — теплопроводность; · Теплопроводность (коэффициент теплопроводности) газа
где cv — удельная теплоемкость газа при постоянном объеме; r — плотность газа; <J> — средняя арифметическая скорость его молекулы; <l> — средняя длина свободного пробега молекул. · Закон Фика
где Dm — масса газа, перенесенная в результате диффузии через поверхность площадью S за время Dt; D — диффузия (коэффициент Эффузии); · Диффузия (коэффициент диффузии)
· Связь между молярной (Cm) и удельной (с) теплоемкостями газа
· Молярные теплоемкости при постоянном объеме и постоянном давлении соответственно равны
где i — число степеней свободы; R — молярная газовая постоянная. · Удельные теплоемкости при постоянной объеме и постоянном давлении соответственно равны
· Уравнение Майера
· Показатель адиабаты
· Внутренняя энергия идеального газа
где · Работа, связанная с изменением объема газа, в общем случае вычисляется по формуле
где V1 — начальный объем газа; V2 — его конечный объем. Работа газа: а) при изобарном процессе (p =const)
б) при изотермическом процессе (Т =const)
в) при адиабатном процессе
· Уравнение Пуассона (уравнение газового состояния при адиабатном процессе)
· Первое начало термодинамики в общем случае записывается в виде
где Q — количество теплоты, сообщённое газу; DU — изменение его внутренней энергии; А — работа, совершаемая газом против внешних сил. Первое начало термодинамики: а) при изобарном процессе
б) при изохорном процессе (A =0)
в) при изотермическом процессе (DU =0)
г) при адиабатном процессе (Q =0)
· Термический коэффициент полезного действия (КПД) цикла в общем случае
где Q1 — количество теплоты, полученное рабочим телом (газом) от нагревателя; Q2 — количество теплоты, переданное рабочим телом охладителю. КПД цикла Карно
где T 1 — температура нагревателя; T 2 — температура охладителя. · Изменение энтропии
где A и B — пределы интегрирования, соответствующие начальному и конечному состояниям системы. Так как процесс равновесный, то интегрирование проводится по любому пути. · Уравнение Ван-дер-Ваальса для одного моля газа
для произвольного количества вещества ν газа
где a и b — постоянные Ван-дер-Ваальса (рассчитанные на один моль газа); V – объем, занимаемый газом; Vm — молярный объем; р — давление газа на стенки сосуда. Внутреннее давление, обусловленное силами взаимодействия молекул,
· Связь критических параметров – объема, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса:
· Внутренняя энергия реального газа
где СV — молярная теплоемкость газа при постоянном объеме. Тема 8. Энтропия. (2 ч.) Энтропия и ее статистическая интерпретация. Возрастание энтропии при неравновесных процессах. Неравенство Клаузиуса. Представление о термодинамике открытых систем. Границы применимости второго закона термодинамики и несостоятельность «тепловой смерти вселенной». Статистическое определение энтропии и ее связь с термодинамической вероятностью.
Вопросы для самопроверки: 1. Кто ввел понятие энтропии? Что называют энтропией? 2. Что называют термодинамической вероятностью состояния системы? 3. Как энтропия связана с термодинамической вероятностью состояния системы? 4. Как ведет себя энтропия замкнутой системы? 5. Запишите и поясните неравенство Клаузиуса. 6. Сформулируйте второе начало термодинамики. 7. Сформулируйте теорему Нернста.
Задачи для решения на занятии: 1. Найти изменение ΔS энтропии при изобарном расширении азота массой m =4 г от объема V1 =5 л до объема V2 =9 л 2. Смешали воду массой m1 =5 кг при температуре T1 =280 К с водой массой m2 =8 кг при температуре Т2 =350 К. Найти: 1) температуру θ смеси; 2) изменение ΔS энтропии, происходящее при смешивании. 3. Кусок льда массой m =200 г, взятый при температуре t1 =-10 °С, был нагрет до температуры t2 =0 °С и расплавлен, после чего образовавшаяся вода была нагрета до температуры t= 10 °С. Определить изменение ΔS энтропии в ходе указанных процессов. 4. Водород массой m =100 г был изобарно нагрет так, что объем его увеличился в n =3 раза, затем водород был изохорно охлаждён так, что давление его уменьшилось в n =3 раза. Найти изменение ΔS энтропии в ходе указанных процессов.
Домашнее задание: 1. В результате изохорного нагревания водорода массой m =l г давление р газа увеличилось в два раза. Определить изменение ΔS энтропии газа. 2. Найти изменение DS энтропии при нагревании воды массой m=100 г от температуры t1 =0°C до температуры t2 =100°С и последующем превращении воды в пар той же температуры. 3. Лед массой m1 =2 кг при температуре t1 =0 °С был превращен в воду той же температуры с помощью пара, имеющего температуру t2 =100°С. Определить массу m2 израсходованного пара. Каково изменение ΔS энтропии системы лед–пар? 4. Кислород массой m =2 кг увеличил свой объем в n =5 раз один раз изотермически, другой – адиабатно. Найти изменения энтропии в каждом из указанных процессов. Вопросы для коллоквиума 1. 1. Молекулярная физика и термодинамика. Предмет и методы. Основные параметры состояния системы. 2. Газовые законы (Бойля-Мариотта, Гей-Люссака, Шарля, Авогадро, Дальтона). 3. Уравнение состояния идеального газа Клапейрона-Менделеева. 4. Основное уравнение МКТ. 5. Распределение молекул идеального газа по скоростям (Максвелла). 6. Барометрическая формула, распределение Больцмана. 7. Явления переноса; диффузия, теплопроводность, вязкость. 8. Средняя длина свободного пробега и среднее число столкновений молекул. 9. Внутренняя энергия идеального газа, число степеней свободы молекул. 10. Первое начало термодинамики, теплоемкость (виды, определения, связь). 11. Молярная теплоемкость идеального газа при постоянном объёме и при постоянном давлении. 12. Адиабатический и политропный процессы. 13. Круговые процессы (циклы), КПД. 14. Энтропия. Второе начало термодинамики. 15. Реальные газы, уравнение состояния. 16. Реальные газы, изотермы Ван-дер-Ваальса. 17. Жидкости и их свойства: поверхностное натяжение. 18. Жидкости и их свойства: смачивание. 19. Давление под искривленной поверхностью жидкости. 20. Капиллярные явления. 21. Твердые тела: типы и виды кристаллов. 22. Плавление, кристаллизация, сублимация твердых тел, аморфные тела. 23. Фазовые переходы I и II рода. 24. Диаграмма состояний, тройная точка.
Вопросы для самостоятельной контролируемой работы студентов 1. Температура и термодинамическое равновесие. Температурные шкалы. 2. Способы измерения температуры и виды термометров. 3. Экспериментальное обоснование молекулярно-кинетической теории: основные экспериментальные факты о строении вещества, межмолекулярных взаимодействиях, тепловом движении. 4. Экспериментальное определение средней длины свободного пробега и скорости молекул. 5. Явления в разреженных газах: внутреннее трение и теплопроводность. 6. Методы получения низких температур и сжижение газов. 7. Испарение и кипение жидкостей. Насыщенный пар. Точка росы. Основные законы и формулы.
Электричество · Закон Кулона:
| ||
|
| Поделиться: |


 – единичные векторы направлений (орты), х, у, z – координаты точки.
– единичные векторы направлений (орты), х, у, z – координаты точки.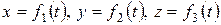
 ,
, - перемещение материальной точки за интервал времени
- перемещение материальной точки за интервал времени  .
. ,
, - путь, пройденный точкой за интервал времени
- путь, пройденный точкой за интервал времени  ,
, - проекции скорости
- проекции скорости  на оси координат
на оси координат
 ,
,
 - проекции ускорения
- проекции ускорения  на оси координат.
на оси координат.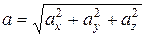
 При криволинейном движении ускорение можно представить как сумму нормальной
При криволинейном движении ускорение можно представить как сумму нормальной  и тангенциальной
и тангенциальной  составляющих.
составляющих.
 ,
, ,
, - время. При равномерном движении
- время. При равномерном движении и
и 
 ) вдоль оси х
) вдоль оси х ,
, - начальная скорость,
- начальная скорость,  - время
- время

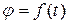
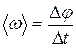 ,
,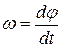

 ,
,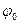 - начальное угловое перемещение;
- начальное угловое перемещение;  и
и 
 или
или  ,
, )
) ,
, - начальная угловая скорость;
- начальная угловая скорость; 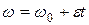
 (
( ;
; ;
;
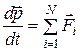 , или
, или 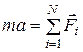 ,
, - геометрическая сумма сил, действующих на материальную точку;
- геометрическая сумма сил, действующих на материальную точку;  - масса;
- масса;  - ускорение;
- ускорение; 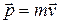 - импульс; N – число сил, действующих на точку;
- импульс; N – число сил, действующих на точку;

 на соответствующие оси координат.
на соответствующие оси координат.
 ,
,

 - ее координаты.
- ее координаты. или
или 
 или
или 
 - угол между направлениями векторов силы
- угол между направлениями векторов силы  и перемещения
и перемещения 
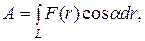


 или
или  ,
,
 или
или 
 или
или 
 - единичные векторы (орты).В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное), то
- единичные векторы (орты).В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное), то
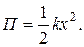

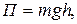



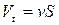
 ,
,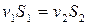 ,
,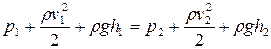 ,
, — плотность жидкости,
— плотность жидкости,  — динамические давления жидкости в двух сечениях, h1 и h2 — высоты этих сечений над некоторым уровнем, g — ускорение свободного падения,
— динамические давления жидкости в двух сечениях, h1 и h2 — высоты этих сечений над некоторым уровнем, g — ускорение свободного падения,  — гидростатические давления;
— гидростатические давления; .
. ,
,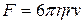 ,
,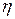 — коэффициент внутреннего трения жидкости, r — радиус шарика, v — его скорость.
— коэффициент внутреннего трения жидкости, r — радиус шарика, v — его скорость. ,
, р — разность давлений на концах трубки.
р — разность давлений на концах трубки. ,
, ,
,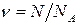
 ,
, ,
,
 ,
, , или
, или  ,
, ,
, ,
, ,
, — средняя кинетическая энергия* поступательного движения молекулы.
— средняя кинетическая энергия* поступательного движения молекулы.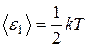 ;
; .
. , или
, или  ;
; , или
, или  ;
; , или
, или 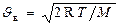 ,
, ,
, или
или  ,
, ,
, .
.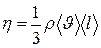

 ,
, — градиент температуры.
— градиент температуры. или
или  ,
, ,
, — градиент концентрации молекул; m1 — масса одной молекулы.
— градиент концентрации молекул; m1 — масса одной молекулы.
 ,где М — молярная масса газа.
,где М — молярная масса газа. ;
; 
 ,
,  .
. .
. или
или  .
. или
или 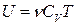 ,
,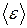 — средняя кинетическая энергия молекулы; N — число молекул газа; v — количество вещества.
— средняя кинетическая энергия молекулы; N — число молекул газа; v — количество вещества. ,
, ;
;
 или
или 
 .
. ,
,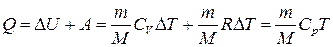
 ;
; ,
, .
. ,
, ,
,
 ,
, ,
,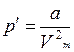 или
или  .
. ;
;  ;
;  .
. ,
, ,
, .
.


