
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ поляризованного света. Закон МалюсаСодержание книги
Поиск на нашем сайте
Анализ поляризованного света осуществляется с помощью поляризационных приборов. Если поляризационный прибор используется для получения поляризованного света, то он называется поляризатором. При использовании прибора для анализа поляризованного света его называют анализатором. Если на пути естественного света поставить поляризатор, то из него выйдет плоскополяризованный свет, интенсивность которого I о составит половину интенсивности естественного света I ест:
Рассчитаем интенсивность света на выходе из второго поляризатора (анализатора). Пусть АА’ (рис.3) – плоскость, в которой колеблется световой вектор Из рисунка видно, что
где I – интенсивность света на выходе из анализатора. Эта формула известна, как закон Малюса.
Рис.3
Интенсивность света I будет максимальной в том случае, когда Реально прохождение света через анализатор и поляризатор связано с потерями световой энергии, т.е. световой луч при выходе из них имеет интенсивность меньшую чем Если поляризатор вращать вокруг направления луча, то для частично поляризованного света наблюдается изменение интенсивности от I max до I min. Выражение
называется степенью поляризации. Для плоскополяризованного света I min = 0 и Р = 1.
Прохождение плоскополяризованного Света через кристаллическую пластинку Пусть поляризованный свет падает перпендикулярно на кристаллическую пластинку толщиной d. Пластинка вырезана из кристалла так, что оптическая ось кристалла параллельна ее поверхности. Угол между плоскостью колебаний вектора Колебания вектора Внутри кристалла падающий луч разделится на «обыкновенный» и «необыкновенный» лучи, амплитуды светового вектора в которых будут равны:
Скорости распространения лучей в пластинке различны, поэтому внутри пластинки между ними накопится дополнительная разность фаз колебаний векторов
Рис.4
Эту разность фаз можно найти следующим образом. Поскольку волны входят в кристалл перпендикулярно его оптической оси, то их геометрические пути в кристалле будут одинаковы и равны толщине кристалла. Вместе с тем оптические длины путей для «обыкновенного» и «необыкновенного» лучей из-за различия в показателях преломления будут различны. Следовательно, возникающая в кристалле оптическая разность хода волн равна
Отсюда разность фаз, накопленная внутри пластинки
где k – волновое число; l -длина волны падающего излучения в вакууме. Вид поляризации на выходе из кристаллической пластинки определяется общей разностью фаз
В общем случае возникает эллиптически поляризованный свет. Причем форма и ориентация эллипса зависят от величины угла a и разности фаз (6) при одном и том же угле a.
Описание установки приведено в приложении «Краткое описание МУК-О» Задание к работе
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 783; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.116.34 (0.005 с.) |

 .
. в волне, выходящей из первого поляризатора (плоскость главного сечения поляризатора); ВВ’ – плоскость главного сечения анализатора. Колебания
в волне, выходящей из первого поляризатора (плоскость главного сечения поляризатора); ВВ’ – плоскость главного сечения анализатора. Колебания  в луче, выходящем из анализатора, происходят в плоскости ВВ’.
в луче, выходящем из анализатора, происходят в плоскости ВВ’.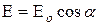 . Так как интенсивность света пропорциональна квадрату напряженности поля, получаем
. Так как интенсивность света пропорциональна квадрату напряженности поля, получаем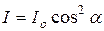 , (2)
, (2)
 (главные сечения поляризатора и анализатора параллельны). При
(главные сечения поляризатора и анализатора параллельны). При  интенсивность света на выходе из анализатора равна нулю, т.е. скрещенные поляризаторы света не пропускают.
интенсивность света на выходе из анализатора равна нулю, т.е. скрещенные поляризаторы света не пропускают. (3)
(3) этих взаимно перпендикулярных колебаний. При разности фаз
этих взаимно перпендикулярных колебаний. При разности фаз  и
и  радиан падающая на кристалл волна будет плоскополяризованной; При разности фаз
радиан падающая на кристалл волна будет плоскополяризованной; При разности фаз 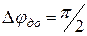 и
и  радиан – поляризованной по эллипсу.
радиан – поляризованной по эллипсу. (4)
(4) и
и  .
.
 . (5)
. (5) , (6)
, (6) .
.


