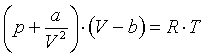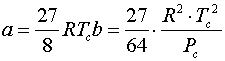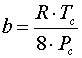Переход из газообразного состояния в жидкое. Область 2-х фазных состояний. Критическое состояние и его свойства. Экспериментальные изотермы.

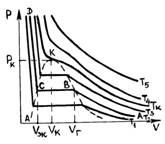
Конденса́ция паров (лат. condense — уплотняю, сгущаю) — переход вещества в жидкое или твёрдое состояние из газообразного. Максимальная температура, ниже которой происходит конденсация, называется критической. Пар, из которого может происходить конденсация, бывает насыщенным или ненасыщенным.

Конденсация насыщенных паров

При наличии жидкой фазы вещества конденсация происходит при сколь угодно малых пересыщениях и очень быстро. В этом случае возникает подвижное равновесие между испаряющейся жидкостью и конденсирующимися парами. Уравнение Клапейрона — Клаузиуса определяет параметры этого равновесия — в частности, выделение тепла при конденсации и охлаждение при испарении.

Критическое состояние и его свойства.

состояние вещества в точках фазовых переходов II рода. К. с., являющееся предельным случаем равновесия двухфазных систем, наблюдается в чистых веществах при равновесии жидкость — газ, а в растворах — при фазовых равновесиях газ — газ, жидкость — жидкость, жидкость — газ, твёрдое тело — твёрдое тело. На диаграммах состояния К. с. соответствуют предельные точки на кривых равновесия фаз (рис. 1, а и б) — т. н. критические точки.Согласно фаз правилу критическая точка изолирована в случае двухфазного равновесия чистого вещества, а, например, в случае бинарных (двойных) растворов критические точки образуют критическую кривую в пространстве термодинамических переменных (параметров состояния). Значения параметров состояния, соответствующие К. с., называются критическими — критическое давление рк, критическая температура Тк, критический объём Vк.

В двухкомпонентных системах характерные для К. с. явления наблюдаются не только в критической точке равновесия жидкость — газ, но и в так называемых критических точках растворимости, где взаимная растворимость компонентов становится неограниченной. Существуют двойные жидкие системы как с одной, так и с двумя критическими точками растворимости — верхней и нижней (рис. 2, а и б). Эти точки являются температурными границами области расслаивания жидких смесей на фазы различного состава. Аналогичной способностью к расслаиванию при определённой критической температуре обладают некоторые растворы газов и твёрдые растворы.

При приближении к К. с. физические свойства вещества резко изменяются: теоретически неограниченно возрастает теплоёмкость и восприимчивость системы к внешним воздействиям (например, изотермическая сжимаемость в случае чистых жидкостей, магнитная восприимчивость у ферромагнетиков и т. д.); наблюдается целый ряд др. особенностей в поведении вещества (см. Критические явления). Эти особенности, характерные для К. с. объектов самой различной природы, объясняются тем, что свойства вещества в К. с. определяются не столько конкретными законами взаимодействия его частиц, сколько резким возрастанием в веществе флуктуаций и радиуса их корреляции. Знание особых свойств веществ в К. с. необходимо во многих областях науки и техники: при создании энергетических установок на сверхкритических параметрах, сверхпроводящих систем, установок для сжижения газов, разделения смесей и т. д

Экспериментальные изотермы.

Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой сложными силами взаимодействия. При высоких давлениях и достаточно низких температурах реальные газы конденсируются, т. е. переходят в жидкое состояние, чего принципиально не может быть с идеальными газами.

рис. 1

 

 

58.

Уравнение Ван-дер-Вальса.Изотермы газа Ван-дер-Вальса.

Уравнение Ван-дер-Ваальса (van der Waals J.D.) является наиболее известным аналитическим уравнением состояния реального газа:

 

Обозначения

R - универсальная газовая постоянная

P - давление

Pc - критическое давление

T - температура

Tc - критическая температура

V - мольный объем

Vc - критический мольный объем