
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 4. 1 момент силы и момент инерцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Основная задача динамики вращательного движения - определение угловых координат точек вращающегося тела в любой момент времени по известным начальным угловым координатам, угловым скоростям и по заданным моментам внешних сил, действующих на тело. Твёрдое тело – тело, все части которого неизменно сохраняют своё расположение; конфигурация частей твёрдого тела не изменяется даже при действии внешних сил. В частности, неизменными остаются расстояния между его частями. Это идеальное представление об абсолютно твёрдом теле (см. определение в § I.1.1). В реальности же все существующие в природе твёрдые тела деформируются под действием сил, однако, деформации многих твёрдых тел очень малы относительно прикладываемых к ним сил и поэтому мы можем смело пользоваться упрощённой моделью абсолютно твёрдого тела. Абсолютно твёрдое тело, имеющее закреплённую ось вращения, без воздействия моментов внешних сил не изменяет угловой скорости вращательного движения. При этом в инерциальной системе отсчёта тело либо покоится ( Вращение тела вокруг оси под действием одной силы где Моментом силы относительно неподвижной точки
Момент силы является псевдовектором, его направление совпадает с направлением поступательного движения правого винта при его вращении от радиус-вектора Модуль момента силы:
За единицу вращающего момента в СИ принимается момент силы в 1Н, линия действия которой находится на расстоянии 1 м от оси вращения. Эту единицу называют ньютон – метром (Н·м). Суммарный момент нескольких сил, действующих на тело, равен алгебраической сумме моментов всех сил относительно данной оси:
Если моментам сил, вызывающим вращение тела вокруг оси по часовой стрелке, приписать положительный знак, а моментам сил, вызывающим вращение против часовой стрелки, - отрицательный знак, то условие равновесия тела, имеющего ось вращения, можно сформулировать в виде правила моментов. Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
Общее условие равновесия тел: тело находится в равновесии, если равны нулю геометрическая сумма векторов всех приложенных к нему сил и алгебраическая сумма моментов этих сил относительно оси вращения. Моментом инерции материальной точки относительно данной оси называется физическая величина
Рассматривая твёрдое тело как систему неизменно соединённых между собой материальных точек с массами
Исходя из формулы (I.100), можно дать следующее определение момента инерции тела. Моментом инерции тела (механической системы) относительно неподвижной оси называется физическая величина В случае непрерывного распределения масс эта сумма сводится к интегралу вида:
где Из формул (I.100) и (I.101) следует, что момент инерции тела зависит от: § его массы; § распределения массы относительно данной оси. Момент инерции является мерой инертности тела при вращательном движении. Он играет такую же роль, что и масса при описании поступательного движения тела. Но если масса данного тела считается величиной постоянной, то момент инерции данного тела зависит от положения оси вращения. Кроме того, на момент инерции влияют форма и размеры тела. Согласно теореме Гюйгенса – Штейнера (теореме о переносе осей инерции): момент инерции тела
Из теоремы Гюйгенса – Штейнера, следует, что: q параллельное смещение оси вращения, проходящей через центр масс, приводит к увеличению момента инерции данного тела; q момент инерции тела минимален, если ось вращения проходит через центр масс: q оси, проходящие через точку Формула (I.101), позволяет рассчитать моменты инерции тел простейшей формы относительно некоторых осей.
1. Момент инерции однородного прямого тонкого цилиндрического стержня длины
2. Момент инерции однородного сплошного цилиндра (или диска) радиуса
3. Момент инерции цилиндра радиуса
4. Момент инерции шара (тонкостенной сферы) радиуса
5. Момент инерции стержня длины
6. Момент инерции полого тонкостенного цилиндра радиуса
7. Момент инерции цилиндра с отверстием (колесо, муфта):
где
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |

 ), либо вращается с постоянной угловой скоростью, одинаковой для всех точек тела
), либо вращается с постоянной угловой скоростью, одинаковой для всех точек тела  и
и  .
. может быть остановлено действием второй силы
может быть остановлено действием второй силы  (рис.33). Если две силы
(рис.33). Если две силы  ;
;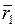 и
и  - радиус-вектор (плечо силы – кратчайшее расстояние от оси вращения до линии действия силы). Из рисунка 35следует, что
- радиус-вектор (плечо силы – кратчайшее расстояние от оси вращения до линии действия силы). Из рисунка 35следует, что 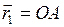 а
а  .
. называется физическая величина, определяемая векторным произведением радиус-вектора
называется физическая величина, определяемая векторным произведением радиус-вектора  , проведённого из точки
, проведённого из точки  и
и  ), на силу
), на силу  :
: (I.96)
(I.96)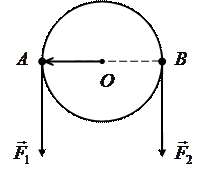
 (I.97)
(I.97)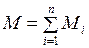 . (I.98)
. (I.98)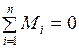 .
. , равная произведению массы точки на квадрат её расстояния
, равная произведению массы точки на квадрат её расстояния 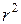 от оси:
от оси: . (I.99)
. (I.99) , расположенных на расстояниях
, расположенных на расстояниях  от оси вращения (рис.34). Каждая из этих точек имеет свой момент инерции
от оси вращения (рис.34). Каждая из этих точек имеет свой момент инерции  ; сумму моментов инерции всех точек, составляющих данное тело, будем называть
; сумму моментов инерции всех точек, составляющих данное тело, будем называть  ; или
; или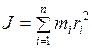 . (I.100)
. (I.100)
 материальных точек тела (системы) на квадраты их расстояний до оси.
материальных точек тела (системы) на квадраты их расстояний до оси. , (I.101)
, (I.101)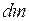 - масса малого элемента объёма тела. Пределы интегрирования определяются формой и размерами тела.
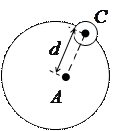
- масса малого элемента объёма тела. Пределы интегрирования определяются формой и размерами тела. (рис. 35) относительно произвольной оси равен сумме момента инерции этого тела
(рис. 35) относительно произвольной оси равен сумме момента инерции этого тела  относительно оси, проходящей через центр инерции тела (центр масс) параллельно рассматриваемой оси, и произведения массы тела
относительно оси, проходящей через центр инерции тела (центр масс) параллельно рассматриваемой оси, и произведения массы тела 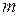 на квадрат расстояния
на квадрат расстояния  между осями:
между осями: .
.
 ;
; ), должны быть параллельны.
), должны быть параллельны. и массы
и массы 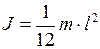 . (I.102)
. (I.102)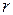 и массы
и массы 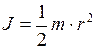 . (I.103)
. (I.103) относительно оси, перпендикулярной к его высоте и проходящей через её середину:
относительно оси, перпендикулярной к его высоте и проходящей через её середину: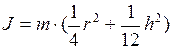 . (I.104)
. (I.104) . (I.105)
. (I.105) . (I.106)
. (I.106)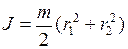 , (I.108)
, (I.108)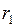 и
и  - радиусы цилиндра и отверстия в нём.
- радиусы цилиндра и отверстия в нём.


