
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 6. 4 внутреннее трение в жидкостяхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Внутреннее трение возникает в жидкости вследствие взаимодействия молекул. В отличие от внешнего трения, возникающего в месте соприкосновения двух тел, внутреннее трение имеет место внутри движущейся среды между слоями с различными скоростями движения. При скоростях выше критической скорости слои, близкие к стенкам, заметно отстают вследствие трения от средних, возникают значительные разности скоростей, что влечёт за собой образование вихрей. Итак, вязкость, или внутреннее трение в жидкостях, обусловливает не только потери энергии на трение, но ещё и новые образования – вихри. Ньютон установил, что сила вязкости, или внутреннего трения,
где Чтобы выяснить физический смысл Единица СИ динамической вязкости
Единица, допускавшаяся к применению до 1980 г.: пуаз (П), по имени французского учёного Пуазейля, который один из первых (1842 г.) начал точные исследования вязкости при течении жидкостей в тонких трубках (соотношение между единицами динамической вязкости: 1 П = 0,1 Па·с) Пуазейль, наблюдая движение жидкостей в капиллярных трубках, вывел закон, согласно которому:
где
Чем больше вязкость, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причём характер этой зависимости для жидкостей и газов различен: q динамическая вязкость жидкостей резко уменьшается с повышением температуры; q динамическая вязкость газов увеличивается с повышением температуры. Кроме понятия динамической вязкости применяются понятия текучести и кинематической вязкости. Текучестью
Единица СИ текучести Кинематической вязкостью
Единица СИ кинематической вязкости До 1980 г. к применению допускалась единица: стокс (Ст). Соотношение между единицами кинематической вязкости: 1 стокс (Ст) = 10 –4 м2/с. Когда тело шарообразной формы движется в жидкости, ему приходится преодолевать силу трения:
Формула (I.153) представляет собой закон Стокса. На законе Стокса основано определение вязкости жидкости вискозиметром Гёпплера. В трубу определённого диаметра, заполненную жидкостью, вязкость которой надо определить, опускают шарик и измеряют скорость его падения, которая и является мерой вязкости жидкости. Английский учёный О. Рейнольдс в 1883 г. в результате своих исследований пришёл к заключению, что критерием характеризующем движение жидкостей и газов, могут служить числа, определяемые безразмерной совокупностью величин, относящихся к данной жидкости и данному её движению. Состав этих отвлечённых чисел, называемых числами Рейнольдса, таков:
где
Оказалось, что именно такая совокупность величин, определяющих состояние жидкости или газа, служит надёжной характеристикой их движения. Часто используют другую, более удобную запись числа
где Итак, вычисляя числа Рейнольдса для разных жидкостей и газов, нашли, что переход от ламинарного к турбулентному движению происходит для всех них при определённом значении числа Рейнольдса, именно, если Это условие имеет смысл только тогда, когда обеспечено с самого начала спокойное течение; если же оно механически уже возмущено (например, при падении жидкости из резервуара в трубу), то к его изучению предыдущая теория неприменима.
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |

 должна быть пропорциональна градиенту скорости
должна быть пропорциональна градиенту скорости  (величина, показывающая, как быстро меняется скорость при переходе от слоя к слою в направлении
(величина, показывающая, как быстро меняется скорость при переходе от слоя к слою в направлении  , перпендикулярном направлению движения слоёв) и площади
, перпендикулярном направлению движения слоёв) и площади  , на которой обнаруживается действие этой силы. Таким образом, мы приходим к формуле Ньютона:
, на которой обнаруживается действие этой силы. Таким образом, мы приходим к формуле Ньютона: , (I.149)
, (I.149)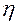 - коэффициент вязкости, или внутреннего трения, постоянное число, характеризующее данную жидкость или газ.
- коэффициент вязкости, или внутреннего трения, постоянное число, характеризующее данную жидкость или газ.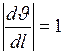 сек –1,
сек –1,  м2; тогда численно
м2; тогда численно  ; следовательно, коэффициент вязкости равен силе трения, которая возникает в жидкости между двумя площадками в
; следовательно, коэффициент вязкости равен силе трения, которая возникает в жидкости между двумя площадками в  м2, если между ними градиент скорости равен единице.
м2, если между ними градиент скорости равен единице. = паскаль - секунда (Па·с).
= паскаль - секунда (Па·с). , (I.150)
, (I.150)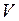 - объём жидкости, протекающий по трубке за время
- объём жидкости, протекающий по трубке за время  ;
;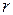 - радиус трубки (с гладкими стенками);
- радиус трубки (с гладкими стенками); - разность давлений на концах трубки;
- разность давлений на концах трубки; называется величина, обратная динамической вязкости.
называется величина, обратная динамической вязкости. . (I.151)
. (I.151) =м2/(Н·с)=1/(Па·с).
=м2/(Н·с)=1/(Па·с). называется отношение динамической вязкости к плотности среды.
называется отношение динамической вязкости к плотности среды. . (I.152)
. (I.152) м2/с.
м2/с. . (I.153)
. (I.153) , (I.154)
, (I.154) - линейный размер (например, диаметр) трубы;
- линейный размер (например, диаметр) трубы;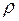 - плотность жидкости;
- плотность жидкости; - средняя по сечению трубы скорость жидкости;
- средняя по сечению трубы скорость жидкости; - динамическая вязкость;
- динамическая вязкость; - безразмерное отвлечённое число.
- безразмерное отвлечённое число. , (I.155)
, (I.155) (или
(или  ), то ламинарное движение устойчиво; если
), то ламинарное движение устойчиво; если  , то ламинарное движение может стать неустойчивым и легко переходит в турбулентное.
, то ламинарное движение может стать неустойчивым и легко переходит в турбулентное.


