
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 7. 5 релятивистская динамикаСодержание книги
Поиск на нашем сайте Все уравнения физики могут быть выражены в инвариантной форме. Этот постулат глубоко связан с дорелятивистским представлением об однородности и изотропности пространства. Что это значит? Будут ли уравнения одного и того же движения иметь одинаковый вид в двух системах координат, повёрнутых друг относительно друга? Конечно, нет. Если в старой системе уравнение было только по оси Уравнения Ньютона инвариантны по отношению к рассматриваемому так называемому галилеевскому преобразованию. Если начальные условия взять в обеих системах одинаковыми, то и движения будут одинаковы. Значит, существует бесконечное множество систем, движущихся прямолинейно и равномерно относительно исходной системы (и относительно друг друга), в которых законы механики одинаковы. Этот принцип относительности равномерного поступательного движения можно формулировать двояко: 1. уравнения Ньютона инвариантны при галилеевском преобразовании; 2. все механические явления при одинаковых начальных условиях протекают одинаково во всех системах, движущихся прямолинейно и равномерно относительно инерциальных систем. Классическая физика отождествляла оба утверждения, так как считала галилеевское преобразование единственно справедливым. До теории относительности обе формулировки просто сливались. Теория же относительности, полностью сохраняя положение 2, отрицает справедливость и уравнений Ньютона и преобразование Галилея. То, что механический принцип относительности равномерного прямолинейного движения действительно является физическим законом, видно уже из того, что он не распространяется на ускоренно движущиеся системы отсчёта. В связи с этим ещё одно замечание. Когда мы говорим, что все механические явления протекают в двух инерциальных системах одинаково, мы предполагаем, что все условия повторены в обеих системах. Принцип относительности механики, мы дали в двух формулировках. Первая чисто математическая, говорит о том, что ньютоновы уравнения инвариантны по отношению к преобразованиям Галилея. Вторая, гораздо более общая, опирается на предположение, что преобразование Галилея характеризует движение одной системы относительно другой, отображает физический процесс. Тогда принцип относительности механики означает, что существует бесчисленное множество систем, движущихся друг относительно друга прямолинейно и равномерно, в которых при одинаковых начальных условиях все механические явления протекают одинаково. Это уже физическое утверждение. Следствием его и является классический закон сложения скоростей, о котором мы говорили в §I.7.4 (С). Динамика, основанная на постулатах специальной теории относительности, инвариантная относительно преобразований Лоренца, называется релятивистской динамикой. Поскольку Основной закон релятивистской динамики – вектор результирующей силы
А. Релятивистская масса
В специальной теории относительности под массой понимают равенство:
где Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то В. Релятивистский импульс
Для релятивистского импульса
где
Частицы с массой покоя С. Преобразование энергии Закон взаимосвязи массы и энергии: полная энергия
где Наименьшей энергией
Энергия покоя тела является его внутренней энергией. Она состоит из суммы энергий покоя всех частиц тела, кинетической энергии всех частиц относительно общего центра масс и потенциальной энергии их взаимодействия. В релятивистской механике несправедлив закон сохранения массы покоя. Несохранение массы покоя не означает нарушения закона сохранения массы вообще. В теории относительности справедлив закон сохранения релятивистской массы. Он вытекает из формулы закона взаимосвязи массы и энергии (I.173). В изолированной системе тел сохраняется полная энергия. Следовательно, сохраняется и релятивистская масса. В теории относительности законы сохранения энергии и релятивистской массы взаимосвязаны и представляют собой единый закон сохранения массы и энергии. Однако из этого закона не следует возможность преобразования массы в энергию и обратно. Масса и энергия представляют собой два качественно различных свойства материи не «эквивалентных» друг другу. Превращение энергии системы из одной формы в другую сопровождается превращением массы. Кинетическая энергия
где У релятивистских частиц кинетическая энергия значительно превышает энергию покоя (
Между полной энергией тела
Для релятивистских частиц, таких, у которых
ЧАСТЬ II. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

 , то в новой может быть не только по оси
, то в новой может быть не только по оси  , но и по осям
, но и по осям  и
и  . При преобразовании значения координат изменяются, так что, если подставить числа, уравнения будут другие. Инвариантность заключается не в этом. Она состоит в том, что если поместить рассматриваемое тело относительно новой системы координат точно так же, как раньше относительно старой, то уравнения в новой системе будут тождественны уравнениям в старой. В этом и состоит однородность и изотропность пространства, наличие которых требует, чтобы один и тот же опыт мог быть воспроизведён в разных координатных системах.
. При преобразовании значения координат изменяются, так что, если подставить числа, уравнения будут другие. Инвариантность заключается не в этом. Она состоит в том, что если поместить рассматриваемое тело относительно новой системы координат точно так же, как раньше относительно старой, то уравнения в новой системе будут тождественны уравнениям в старой. В этом и состоит однородность и изотропность пространства, наличие которых требует, чтобы один и тот же опыт мог быть воспроизведён в разных координатных системах. , из классической механики следует, что в том случае, когда тело в течение достаточно длительного времени испытывает ускорение, оно может приобрести любую скорость, даже превышающую скорость света. Это противоречие разрешается, если учесть, что ускорение не инвариантно относительно преобразований Лоренца, т.к. масса (наряду с длиной и временем) также испытывает релятивистские изменения.
, из классической механики следует, что в том случае, когда тело в течение достаточно длительного времени испытывает ускорение, оно может приобрести любую скорость, даже превышающую скорость света. Это противоречие разрешается, если учесть, что ускорение не инвариантно относительно преобразований Лоренца, т.к. масса (наряду с длиной и временем) также испытывает релятивистские изменения. , приложенной к материальной точке (телу), равен изменению вектора импульса
, приложенной к материальной точке (телу), равен изменению вектора импульса  материальной точки тела (или тела) за единицу времени.
материальной точки тела (или тела) за единицу времени. . (I.170)
. (I.170) , (I.171)
, (I.171) — полная энергия свободного тела,
— полная энергия свободного тела,  — его импульс,
— его импульс,  — скорость света (
— скорость света ( м/с).
м/с). — масса определяется энергией покоя. В некоторых источниках, в основном относящихся к началу XX века, а также научно-популярных [10], введённое выше понятие массы называют «массой покоя», при этом саму массу вводят на основе классического определения импульса:
— масса определяется энергией покоя. В некоторых источниках, в основном относящихся к началу XX века, а также научно-популярных [10], введённое выше понятие массы называют «массой покоя», при этом саму массу вводят на основе классического определения импульса: 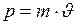 . В таком случае
. В таком случае  и говорят, что масса тела растёт с увеличением скорости. При таком определении понятие массы фактически подменяет понятие энергии, а также требуется отдельно вводить «массу покоя», измеряемую в собственной СО, и «релятивистскую массу» движущегося тела. Такой подход был распространён на заре становления СТО, так как позволял провести многочисленные аналогии с классической физикой, однако в современной науке нежелателен и не используется, так как вносит дополнительную путаницу в терминологии, не давая никаких новых результатов. Так называемая релятивистская масса оказывается аддитивной (в отличие от массы покоя системы, зависящей от состояния составляющих её частиц). Однако безмассовые частицы (например, фотоны) в такой терминологии оказываются имеющими переменную массу; кроме того, релятивистская масса ничуть не упрощает формулировку законов динамики частиц. Использование этих понятий в современной физике нежелательно.
и говорят, что масса тела растёт с увеличением скорости. При таком определении понятие массы фактически подменяет понятие энергии, а также требуется отдельно вводить «массу покоя», измеряемую в собственной СО, и «релятивистскую массу» движущегося тела. Такой подход был распространён на заре становления СТО, так как позволял провести многочисленные аналогии с классической физикой, однако в современной науке нежелателен и не используется, так как вносит дополнительную путаницу в терминологии, не давая никаких новых результатов. Так называемая релятивистская масса оказывается аддитивной (в отличие от массы покоя системы, зависящей от состояния составляющих её частиц). Однако безмассовые частицы (например, фотоны) в такой терминологии оказываются имеющими переменную массу; кроме того, релятивистская масса ничуть не упрощает формулировку законов динамики частиц. Использование этих понятий в современной физике нежелательно. . (I.172)
. (I.172) - масса покоя тела (собственная масса);
- масса покоя тела (собственная масса); - скорость тела относительно системы отсчёта;
- скорость тела относительно системы отсчёта; (
(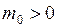 могут достичь только скорости, меньшей скорости света
могут достичь только скорости, меньшей скорости света  . Частицы с нулевой массой покоя
. Частицы с нулевой массой покоя  всегда движутся со скоростью
всегда движутся со скоростью  .
.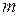 :
: , (I.173)
, (I.173) тело (частица) обладает в системе отсчёта, относительно которой оно покоится
тело (частица) обладает в системе отсчёта, относительно которой оно покоится  . Энергия
. Энергия  . (I.174)
. (I.174) свободного тела (частицы) представляет собой разность между полной энергией тела
свободного тела (частицы) представляет собой разность между полной энергией тела  , (I.175)
, (I.175) .
. . (I.176)
. (I.176)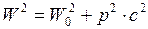 . (I.177)
. (I.177) , т.е.
, т.е.  , справедливо соотношение:
, справедливо соотношение: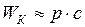 . (I.178)
. (I.178)


