
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава II. 7 элементы специальной теории относительностиСодержание книги
Поиск на нашем сайте II.7.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
1. Преобразования Лоренца
где предполагается, что система отсчёта
2. Релятивистское замедление хода часов
где
3. Релятивистское (лоренцево) сокращение длины
где
4. Релятивистский закон сложения скоростей
где предполагается, что система отсчёта 5. Масса релятивистской частицы
где
6. Релятивистский импульс частицы
7. Основной закон релятивистской динамики
где
8. Закон взаимосвязи массы и энергии
где
9. Связь между энергией и импульсом релятивистской частицы
где 10. Кинетическая энергия
II.7. 2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА № II.118 Согласуется ли с принципами специальной теории относительности представление о теле в виде шара радиуса Ответ. Нет, не согласуется. Скорость экваториальных точек такого тела ЗАДАЧА № II.119 Согласуется ли с принципами специальной теории относительности представление об электроне как о вращающемся вокруг своей оси однородном шарике массы Ответ. Нет, не согласуется, так как скорость на «экваторе» такого шарика была бы равна
ЗАДАЧА № II.120 Имеются два одинаковых стержня. Стержень 1 покоится в системе отсчёта Ответ. А)Стержень 2. Б) стержень 1.
ЗАДАЧА № II.121 При каких условиях справедливы преобразования Галилея? преобразования Лоренца? Ответ. Преобразования Галилея справедливы для скоростей, малых по сравнению со скоростью света в вакууме. Преобразования Лоренца справедливы и для скоростей, близких к скорости света в вакууме. ЗАДАЧА № II.122 Зависит ли от скорости движения системы отсчёта скорость тела? скорость света? Ответ. Скорость тела зависит от выбора системы отсчёта; скорость света в вакууме не зависит от выбора системы отсчёта и во всех инерциальных системах отсчёта одинакова.
ЗАДАЧА № II.123 Неподвижный наблюдатель 1, находившийся посредине между точками
Ответ. Нет. Для наблюдателя 2 в точку ЗАДАЧА № II.124 В тотмомент, когда середина поезда, движущегося равномерно и прямолинейно, проходит мимо наблюдателя
Ответ. Нет. Так как поезд движется в точке ЗАДАЧА № II.125 По условию задачи № II.118определить, какой фонарь для наблюдателя Ответ: 1) фонарь
ЗАДАЧА № II.126 Какой стала бы длина тела по направлению движения относительно неподвижного наблюдателя при Ответ. Из формулы ЗАДАЧА № II.127 Что можно сказать о длине стержня в различных инерциальных системах отсчёта? Имеет ли смысл понятие «длина стержня» вне связи с системой отсчёта? Ответ. Длина стержня в различных системах отсчёта неодинакова. Понятие длины стержня имеет смысл только в конкретной системе отсчёта. ЗАДАЧА № II.128 Какую скорость должно иметь тело, чтобы его продольные размеры уменьшились для неподвижного наблюдателя Дано:
Найти: Решение
Относительно наблюдателя
где Выразим из уравнения (1) скорость движения тела, предварительно возведя обе части равенства в квадрат, получим:
т.е. скорость тела должна составлять
ЗАДАЧА № II.129 Какова должна быть энергия частицы, чтобы её продольный размер стал в Дано:
Найти: Решение
Кинетическая энергия частицы определяется по формуле:
Преобразуем уравнение (1) к виду:
Относительно наблюдателя
Выразим из формулы (3)
Подставим формулу (4), в формулу (2), получим:
ЗАДАЧА № II.130 При какой относительной скорости движения релятивистское сокращение длины движущегося тела составляет 25%.
Дано: Найти: Решение
Относительно наблюдателя
По условию задачи Таким образом,
ЗАДАЧА № II.131 Ракета движется относительно неподвижного наблюдателя Дано:
Найти: Решение
Время, прошедшее по часам неподвижного наблюдателя, найдём по формуле:
где
В данной задаче время
ЗАДАЧА № II.132 Собственное время жизни частицы отличается на 1% от времени жизни по неподвижным часам. Определите Дано: Найти: Решение
Релятивистское замедление хода часов определяется по формуле:
где
Собственное время жизни частицы отличается от времени жизни по неподвижным часам на величину
Перепишем формулу (2) в виде:
Выразим
Из формулы (4), определим
ЗАДАЧА № II.133 Определите зависимость скорости частицы (масса частицы Дано: Найти: Решение
Для нахождения зависимости скорости движения частицы от времени, используем основной закон релятивистской динамики:
Релятивистский импульс частицы определяется формулой:
Приравняем формулы (1) и (2):
Выразим из полученного равенства скорость
Формула (4) и будет устанавливать зависимость скорости движения частицы от времени ЗАДАЧА № II.134 Определите релятивистский импульс и кинетическую энергию протона, движущегося со скоростью
Дано:
Найти: Решение
Релятивистский импульс протона определим по формуле:
Кинетическая энергия
ЗАДАЧА № II.135 Определите работу, которую необходимо совершить, чтобы увеличить скорость частицы от Дано:
Найти: Решение
Работу, которую необходимо совершить, для увеличения скорости частицы, найдём из уравнения:
где
Подставим формулу (2) в формулу (1), получим:
ЗАДАЧА № II.137 С какой скоростью достигают электроны анода рентгеновской трубки, работающей при напряжении 50 кВ? Решить задачу с учётом релятивистской поправки и найти процент ошибки при расчёте, произведённом по классическим формулам.
Дано: Найти:
Решение
Согласно классическим формулам, из закона сохранения энергии имеем:
Из формулы (1), найдём
Согласно релятивистским формулам, из закона сохранения энергии имеем:
Отсюда
Из равенства (3), найдём
Процент ошибки
ЧАСТЬ III. ВОПРОСЫ И ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИ
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |

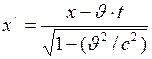 ;
;  ;
;  (I.109)
(I.109)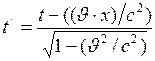 , (I.110)
, (I.110) движется со скоростью
движется со скоростью  в положительном направлении оси
в положительном направлении оси  системы отсчёта
системы отсчёта  , причём оси (
, причём оси ( и
и 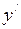 и
и  ), (
), (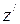 и
и  ) параллельны;
) параллельны; - скорость распространения света в вакууме.
- скорость распространения света в вакууме.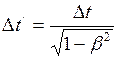 , (I.111)
, (I.111) - интервал времени, между событиями, отсчитанный движущимися вместе с телом часами;
- интервал времени, между событиями, отсчитанный движущимися вместе с телом часами;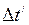 - интервал времени, между теми же событиями, отсчитанный покоящимися часами;
- интервал времени, между теми же событиями, отсчитанный покоящимися часами; .
. , (I.112)
, (I.112) - длина стержня, измеренная в системе отсчёта, относительно которой стержень покоится;
- длина стержня, измеренная в системе отсчёта, относительно которой стержень покоится; - длина стержня, измеренная в системе отсчёта, относительно которой стержень движется со скоростью
- длина стержня, измеренная в системе отсчёта, относительно которой стержень движется со скоростью 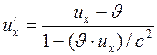 ;
;  ;
; 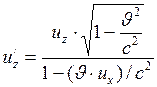 , (I.113)
, (I.113) , (I.114)
, (I.114) - масса покоя тела (собственная масса);
- масса покоя тела (собственная масса);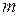 - масса тела, движущегося со скоростью
- масса тела, движущегося со скоростью  (
( м/с).
м/с).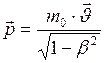 (I.115)
(I.115)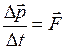 , (I.116)
, (I.116) - релятивистский импульс частицы;
- релятивистский импульс частицы; - вектор результирующей силы, приложенной к частице.
- вектор результирующей силы, приложенной к частице. , (I.117)
, (I.117) - полная энергия свободного тела (частицы);
- полная энергия свободного тела (частицы);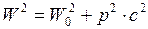 , (I.118)
, (I.118) - энергия покоя.
- энергия покоя. свободного тела (частицы)
свободного тела (частицы) (I.119)
(I.119)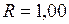 м, вращающегося вокруг своей оси с угловой скоростью
м, вращающегося вокруг своей оси с угловой скоростью  рад/с?
рад/с? м/с превышает скорость света в пустоте.
м/с превышает скорость света в пустоте.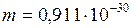 кг (массы электрона) и радиуса
кг (массы электрона) и радиуса 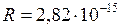 м (классический радиус электрона), обладающем собственным моментом импульса
м (классический радиус электрона), обладающем собственным моментом импульса 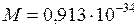 (кг ∙ м2/с) (вытекающее из квантовой теории и подтверждённое экспериментально значение собственного момента импульса электрона)?
(кг ∙ м2/с) (вытекающее из квантовой теории и подтверждённое экспериментально значение собственного момента импульса электрона)?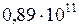 м/с, т.е. превышала бы скорость света в пустоте почти в 300 раз.
м/с, т.е. превышала бы скорость света в пустоте почти в 300 раз.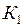 , стержень 2 покоится в системе отсчёта
, стержень 2 покоится в системе отсчёта 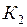 . Системы движутся друг относительно друга вдоль совпадающих осей
. Системы движутся друг относительно друга вдоль совпадающих осей  . Стержни параллельны этим осям. Какой стержень будет короче: а) в системе
. Стержни параллельны этим осям. Какой стержень будет короче: а) в системе  и
и  , увидел, что в эти точки одновременно попали молнии (рис. 87). Одновременны ли эти события для неподвижных наблюдателей 2 и 3? Для каких ещё неподвижных относительно
, увидел, что в эти точки одновременно попали молнии (рис. 87). Одновременны ли эти события для неподвижных наблюдателей 2 и 3? Для каких ещё неподвижных относительно 
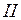 , посредине перрона, одновременно для этого наблюдателя на концах перрона зажигаются фонари
, посредине перрона, одновременно для этого наблюдателя на концах перрона зажигаются фонари 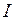 , находящегося в середине движущегося поезда?
, находящегося в середине движущегося поезда?
 ; 2) в точке
; 2) в точке  . Где должен находиться наблюдатель
. Где должен находиться наблюдатель  на таком расстоянии
на таком расстоянии 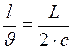 ,
, 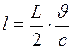 (рис.89).
(рис.89).
 ?
? ,
,  . Следовательно, при
. Следовательно, при 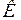 в 3 раза? До этого тело покоилось относительно данного наблюдателя.
в 3 раза? До этого тело покоилось относительно данного наблюдателя.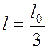 ;
; м/с.
м/с.
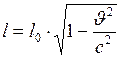 , (1)
, (1)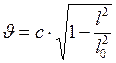 ;
;  ,
,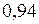 скорости света. Поперечные размеры тела при этом не меняются.
скорости света. Поперечные размеры тела при этом не меняются. раз меньше поперечного?
раз меньше поперечного?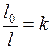 ;
;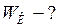
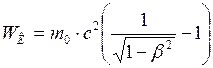 . (2)
. (2)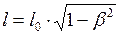 . (3)
. (3) , по условию задачи:
, по условию задачи: 
 . (4)
. (4)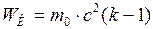 .
.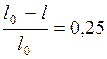
 . Отсюда, следует, что
. Отсюда, следует, что 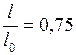 , или
, или  . Подставим это значение в формулу (1), получим:
. Подставим это значение в формулу (1), получим: 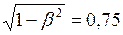 . Значит
. Значит 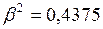 .
.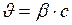 ;
;  км/с.
км/с.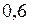 скорости света в вакууме. Какое время пройдёт по часам неподвижного наблюдателя, если по часам, движущимся вместе с ракетой, прошло 6 лет?
скорости света в вакууме. Какое время пройдёт по часам неподвижного наблюдателя, если по часам, движущимся вместе с ракетой, прошло 6 лет?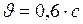 ;
;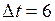 лет;
лет;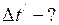
 лет.
лет.

 . (2)
. (2)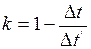 . (3)
. (3)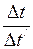 из формулы (1) и подставим в формулу (3):
из формулы (1) и подставим в формулу (3):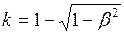 . (4)
. (4) :
: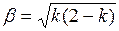 ;
; 
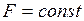 .
.
 ,
, 
 ,
, 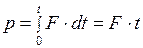 . (1)
. (1)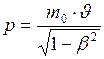 . (2)
. (2)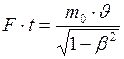 . (3)
. (3)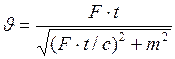 . (4)
. (4)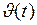 .
.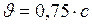 .
. кг;
кг;
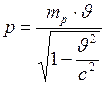 ;
;  (Н·с).
(Н·с).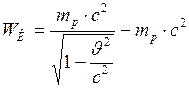 ;
; 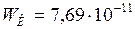 Дж.
Дж.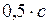 до
до  .
.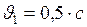 .
.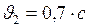

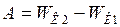 , (1)
, (1)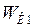 и
и  - начальная и конечная кинетическая энергия частицы. Они соответственно равны:
- начальная и конечная кинетическая энергия частицы. Они соответственно равны: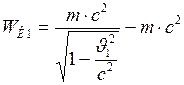 и
и 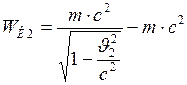 . (2)
. (2)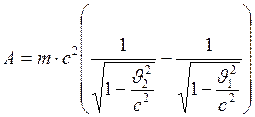 ;
;  .
. кВ.
кВ.
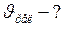
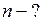
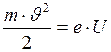 . (1)
. (1)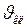 :
: ;
; 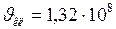 м/с.
м/с.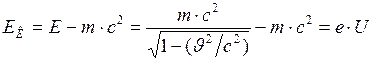 . (2)
. (2)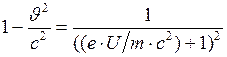 . (3)
. (3) :
: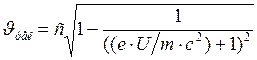 ;
; 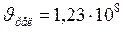 м/с.
м/с. можно определить по формуле:
можно определить по формуле: .
.


