
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава II. 1. Кинематика материальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте II.1.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ 1. Средняя скорость
где
2. Мгновенная скорость
где 3. Среднее ускорение
4. Мгновенное ускорение
5. Скорость для прямолинейного равномерного движения:
6. Путь и скорость для прямолинейного равнопеременного движения:
где В уравнениях (II.6) и (II.8) ускорение положительно при равноускоренном движении и отрицательно при равнозамедленном. 7. Полное ускорение при криволинейном движении
где
где
При вращении тела угол 8. Выражение вида 9. Средняя угловая скорость
где 10. Мгновенная угловая скорость
11. Среднее угловое ускорение
где 12. Мгновенное угловое ускорение
13. Уравнение равномерного вращения:
14. Угловая скорость при равномерном вращательном движении:
15. Угловое ускорение при равномерном вращательном движении:
16. Уравнение равнопеременного вращения:
17. Угловая скорость равнопеременного вращения:
18. Угловое ускорение равнопеременного вращения:
19. Частота вращения (число оборотов в единицу времени):
или
где
20. Связь между линейными и угловыми величинами выражается следующими формулами:
а) длина дуги, пройденная материальной точкой:
где
б) линейная скорость точки:
в) тангенциальное ускорение точки:
г) нормальное ускорение точки:
II.1.2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА № II.1 Вы сидите в одном из вагонов поезда и смотрите в окно. Соседний состав начинает отправляться, а вам кажется, что уходит ваш поезд. Почему? Наблюдалось бы такое явление, если бы вы могли одновременно видеть соседний состав и здание вокзала? Ответ. Потому что невидно тело отсчета. Если бы видели здание вокзала, то такое явление не наблюдалось бы.
ЗАДАЧА № II.2 Автомобиль и троллейбус движутся прямолинейно так, что некоторое время расстояние между ними не меняется. Относительно каких тел, каждый из них в это время находится в покое и относительно каких тел каждый из них движется? Ответ. Автомобиль и троллейбус покоятся относительно друг друга; движутся относительно дороги.
ЗАДАЧА № II.3 Во время сильного снегопада трудно понять, движется поезд или нет. Почему? Ответ. Не видно тела отсчета, относительно которого можно определить, движется поезд или покоится.
ЗАДАЧА № II.4 Летчик-спортсмен сумел посадить небольшой спортивный самолет на крышу легкового автомобиля, движущегося относительно дороги. При каком условии это возможно? Ответ. Скорости самолета и автомобиля должны быть одинаковыми относительно дороги.
ЗАДАЧА № II.5 В метро, на двух эскалаторах стоят пассажиры. Движутся они или покоятся относительно друг друга, если лестницы эскалаторов движутся в одном направлении; движутся в разных направлениях? Ответ. В первом случае пассажиры покоятся относительно друг друга, во втором — пассажиры движутся относительно друг друга.
ЗАДАЧА № II.6 Допустим, что вам нужно перейти улицу под дождем, а зонта у вас нет. Как поступить: бежать или идти шагом? Если вы побежите, то под дождем проведете меньше времени. Однако в этом случае вы можете намокнуть сильнее, чем при ходьбе шагом, так как вы сами набегаете на дождевые струи. Зависит ли ваш ответ от того, какой идет дождь: косой или вертикальный? Ответ. Если дождь идет навстречу или падает вертикально, то следует быстрее бежать к укрытию. ЗАДАЧА № II.7 В первые годы существования авиации самой летной считали погоду с сильным устойчивым ветром. Специальных взлетно-посадочных полос не существовало. Взлетали с более или менее ровного поля и на него же садились. Почему именно в таких условиях подъем и посадка самолетов сопровождались наименьшим числом поломок? Ответ. Для взлета самолета была необходима большая скорость относительно воздуха, а относительно поля, наоборот, — большая скорость была не нужна, так как встречные кочки и другие неровности могли стать причиной опасных поломок. Сильный устойчивый ветер был союзником первых авиаторов именно потому, что он помогал им взлетать и садиться при пониженных скоростях самолета относительно поля.
ЗАДАЧА № II.8 Почему парашют бесполезен при падении с небольшой высоты? Ответ. Раскрытие парашюта и превращение равноускоренного движения парашютиста при падении в равномерное требует времени, в течение которого парашютист успевает пролететь большой путь.
ЗАДАЧА № II.9 С какой целью над колесами велосипеда устанавливаются щитки? Ответ. Грязь, пристающая к колесам, отбрасывается по касательной, поэтому она может попасть в велосипедиста и запачкать велосипед.
ЗАДАЧА № II.10 Во время движения поезда с верхней полки вагона упал мяч. Будет ли он падать вертикально? Какие ответы дадут на этот вопрос наблюдатели, находящиеся в вагоне поезда и на насыпи железной дороги? Ответ. Для наблюдателя, находящегося в вагоне поезда, мяч будет падать вертикально, а для наблюдателя, находящегося на насыпи железной дороги, мяч будет падать по криволинейной траектории. ЗАДАЧА № II.11 Тело переместилось из точки с координатами (0; 2) м в точку с координатами (4; -1) м. Сделать чертёж, найти модуль вектора перемещения тела и его проекции на оси координат. Дано:
Найти: Решение
Из рисунка 48 найдём проекции перемещения на оси координат
Модуль вектора перемещения найдём из прямоугольного треугольника, используя теорему Пифагора:
ЗАДАЧА № II.12 Велосипедист ехал из одного города в другой. Половину пути он ехал со скоростью 12 км/ч. Половину оставшегося времени движения – со скоростью 6 км/ч, а затем до конца пути шёл пешком со скоростью 4 км/ч. Определить среднюю скорость на всём пути (км/ч).
Дано:
Найти:
Решение Среднюю скорость велосипедиста на всём пути определим по формуле:
Так как
Выразим из формулы (2) время
После ряда преобразований, получаем выражение для средней скорости:
ЗАДАЧА № II.13 Два тела движутся под углом Дано: Найти:
Решение
Для нахождения относительной скорости тел, воспользуемся теоремой косинусов:
Расстояние
Для определения угла
ЗАДАЧА № II.14 Из двух точек Дано:
Найти:
Решение
а) Аналитический способ решения. Выберем начало оси
Запишем уравнения движения двух тел:
где
Из уравнения (2) находим время движения тел:
Определим перемещения тел по формулам:
б) Графический способ решения. Отложим в масштабе по оси абсцисс время движения, а по оси ординат – значения координаты
Тогда зависимость координат от времени может быть изображена прямыми 1 и 2 (рис.51).
Найдём координаты их точки пересечения ЗАДАЧА № II.15 При равноускоренном движении из состояния покоя тело проходит за пятую секунду 90 см. Определить перемещение тела за седьмую секунду.
Дано:
Найти: Решение
Проведём ось
Уравнение движения тела имеет вид:
В моменты времени
Аналогичным способом получим формулу для перемещения тела за пятую секунду:
Выразим из формулы (3), ускорение движения тела и подставим его выражение в формулу (2), получим:
ЗАДАЧА № II.16 Уравнение движения тела дано в виде
Дано: Найти: Решение
Данную задачу можно решить двумя способами. 1-й способ. Запишем уравнение движения тела в общем виде:
и сравним его с уравнением движения, которое нам даётся по условию задачи. Очевидно, что Координату тела через 5 с, найдём из уравнения (1): Скорость тела через 5 с определим по формуле: 2-й способ. Координату По определению скорости:
По определению ускорения:
ЗАДАЧА № II.17 Два тела брошены вертикально вверх с земли из одной и той же точки с одинаковой начальной скоростью 19,6 м/с с промежутком времени 0,5 с (рис. 53). Через какое время после бросания второго тела и на какой высоте они встретятся? Дано:
Найти: Решение
Запишем уравнение движения тела в общем виде:
Применительно ко второму телу, оно будет иметь следующий вид:
Тогда уравнение движения первого тела:
В момент встречи двух тел их координаты совпадают, т.е.
Выразим из уравнения (4) время
Высоту
ЗАДАЧА № II.18 Как двигался мотоциклист, график скорости, движения которого изображён на рисунке 54?
Решение
Из графика (рис.54) видно, что мотоциклист начал движение из состояния покоя (точка ЗАДАЧА № II.19 Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Уравнение движения автомобиля
Дано:
Найти: Решение
Запишем общее выражение для скорости движения автомобиля:
Подставим в формулу (1) уравнение движения автомобиля, получим:
Заменим постоянные Для нахождения тангенциального ускорения, воспользуемся формулой (II.10):
Взяв производную по времени от общего уравнения скорости и подставив значения постоянной
Полученное выражение для тангенциального ускорения не содержит времени: это значит, что тангенциальное ускорение постоянно по величине, поэтому движение автомобиля является равнозамедленным. Для нахождения нормального ускорения, используем уравнение (II.11):
Подставим в формулу (4) значения скорости и радиуса кривизны траектории, получим: Полное ускорение определяется по формуле (II.9):
Направление полного ускорения можно определить, если найти угол
ЗАДАЧА № II.20 Колесо вращается по закону Дано:
Найти: Решение
Угловая скорость определяется по формуле (II.13):
Подставим в эту формулу уравнение для углового перемещения:
Используем формулу (II.24) для нахождения линейной скорости:
По определению, угловое ускорение определяется по формуле (II.15):
С учётом уравнения угловой скорости, получим:
Полное ускорение определяется уравнением (II.9):
Тогда
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.017 с.) |

 материальной точки:
материальной точки: , или
, или  , (II.1)
, (II.1) - элементарное приращение точки за промежуток времени
- элементарное приращение точки за промежуток времени  ;
; - путь, пройденный точкой за промежуток времени
- путь, пройденный точкой за промежуток времени  материальной точки:
материальной точки: , или
, или 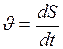 . (II.2)
. (II.2) - радиус-вектор точки.
- радиус-вектор точки. материальной точки:
материальной точки: . (II.3)
. (II.3)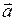 материальной точки:
материальной точки: . (II.4)
. (II.4) . (II.5)
. (II.5) ; (II.6)
; (II.6) ; (II.7)
; (II.7) , (II.8)
, (II.8) - начальная скорость.
- начальная скорость. , (II.9)
, (II.9) - тангенциальное ускорение;
- тангенциальное ускорение; - нормальное (центростремительное) ускорение.
- нормальное (центростремительное) ускорение. ; (II.10)
; (II.10)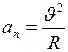 , (II.11)
, (II.11)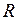 - радиус кривизны траектории в данной точке.
- радиус кривизны траектории в данной точке. есть величина переменная, зависящая от времени
есть величина переменная, зависящая от времени  .
. называется кинематическим уравнением вращения.
называется кинематическим уравнением вращения. материальной точки:
материальной точки: , (II.12)
, (II.12) - изменение угла поворота за время
- изменение угла поворота за время  материальной точки:
материальной точки: . (II.13)
. (II.13) материальной точки:
материальной точки: , (II.14)
, (II.14) - изменение угловой скорости за время
- изменение угловой скорости за время  материальной точки:
материальной точки: . (II.15)
. (II.15) . (II.16)
. (II.16) . (II.17)
. (II.17) . (II.18)
. (II.18) . (II.19)
. (II.19) . (II.20)
. (II.20) . (II.21)
. (II.21) , (II.22)
, (II.22) , (II.23)
, (II.23) - число оборотов, совершаемых за время
- число оборотов, совершаемых за время 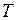 - период вращения (время одного полного оборота).
- период вращения (время одного полного оборота). , (II.24)
, (II.24) ; (II.25)
; (II.25) ; (II.26)
; (II.26) . (II.27)
. (II.27) ;
;  м;
м; м;
м;  =-1 м.
=-1 м. ;
; 
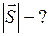

 и
и  :
: ;
; 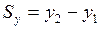 (1)
(1) м;
м;  м.
м. м.
м. км/ч;
км/ч; км/ч;
км/ч; км/ч
км/ч -?
-? . (1)
. (1)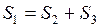 (по условию задачи). Тело движется равномерно, следовательно,
(по условию задачи). Тело движется равномерно, следовательно, 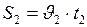 , а
, а  . По условию задачи
. По условию задачи  , значит
, значит . (2)
. (2) , получим:
, получим: . (3)
. (3) ;
;  км/ч.
км/ч. друг к другу со скоростями
друг к другу со скоростями 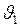 и
и  соответственно. Найти относительную скорость тел
соответственно. Найти относительную скорость тел  и расстояние
и расстояние  между ними в момент времени
между ними в момент времени  по отношению к направлению скорости первого тела
по отношению к направлению скорости первого тела 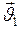 .
. Пусть
Пусть  , где
, где  - относительная скорость тел (рис.49)
- относительная скорость тел (рис.49) . (1)
. (1) . (2)
. (2) , характеризующего направление относительной скорости тел
, характеризующего направление относительной скорости тел  ,
, 
 .
. и
и  , расположенных на расстоянии 90м друг от друга, одновременно в одном направлении начали движение два тела. Тело, движущееся из точки
, расположенных на расстоянии 90м друг от друга, одновременно в одном направлении начали движение два тела. Тело, движущееся из точки  ;
; м;
м;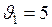 м/с;
м/с; м/с.
м/с.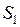 -?
-?  -?
-? 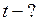
 в точке
в точке 
 ;
;  , (1)
, (1) и
и  - координаты первого и второго тел. В момент встречи двух тел (точка
- координаты первого и второго тел. В момент встречи двух тел (точка  ):
):  . С учётом формулы (1):
. С учётом формулы (1): . (2)
. (2) ;
;  с.
с. ;
;  м;
м; ;
;  м.
м. . Запишем уравнения движения тел (с учётом условия задачи):
. Запишем уравнения движения тел (с учётом условия задачи):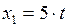 ;
;  . (3)
. (3)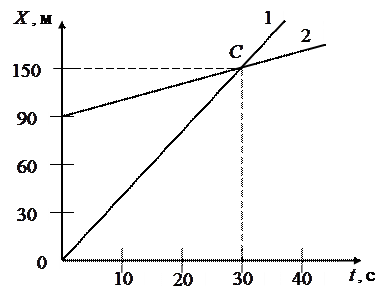

 м. Следовательно, первое тело догонит второе через 30 с. Перемещения тел соответственно равны:
м. Следовательно, первое тело догонит второе через 30 с. Перемещения тел соответственно равны:  м и
м и  м.
м. м;
м;  м/с;
м/с; с;
с;  с;
с; с;
с; 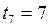 с;
с; см =
см =  м
м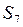 -?
-? , из которой тело начинает движение (рис.52).
, из которой тело начинает движение (рис.52).

 . (1)
. (1) ;
;  . Следовательно, перемещение тела за седьмую секунду будет равно:
. Следовательно, перемещение тела за седьмую секунду будет равно:  или
или . (2)
. (2)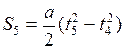 . (3)
. (3) ;
;  м.
м. . Определить начальную скорость и ускорение движения тела, а также координату и скорость тела через 5 с.
. Определить начальную скорость и ускорение движения тела, а также координату и скорость тела через 5 с. с;
с; -?
-? 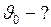


 м/с;
м/с;  м/с2.
м/с2. м.
м. ;
;  м/с.
м/с. ;
;  м/с2.
м/с2. с;
с; м/с
м/с



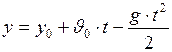 . (1)
. (1) . (2)
. (2) . (3)
. (3) , отсюда следует:
, отсюда следует:
 . (4)
. (4) ; (5)
; (5) с
с найдём, используя формулы (2) и (5):
найдём, используя формулы (2) и (5): ;
;  м.
м.
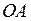 он двигался равноускоренно, на участке
он двигался равноускоренно, на участке  его движение было равномерным, а на участке
его движение было равномерным, а на участке  - равнозамедленным с большим по абсолютному значению ускорением, чем на участке
- равнозамедленным с большим по абсолютному значению ускорением, чем на участке  . Участок
. Участок  соответствует остановке. Участки
соответствует остановке. Участки  ,
,  ,
,  данного графика соответствуют движению мотоциклиста в обратном направлении: участок
данного графика соответствуют движению мотоциклиста в обратном направлении: участок  , где
, где  м,
м,  м/с,
м/с,  м/с2. Найти скорость движения автомобиля; его тангенциальное, нормальное и полное ускорения в момент времени равном 5 с. Определить направление полного ускорения.
м/с2. Найти скорость движения автомобиля; его тангенциальное, нормальное и полное ускорения в момент времени равном 5 с. Определить направление полного ускорения. м;
м;


 . (1)
. (1) . (2)
. (2) и
и  их значениями, получим:
их значениями, получим:  м/с.
м/с. м/с2.
м/с2.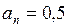 м/с2.
м/с2.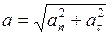 ;
;  м/с2.
м/с2. или
или  .
. . Найти угловую и линейную скорость колеса, а также полное ускорение точек, лежащих на ободе колеса в конце первой секунды вращения. Радиус колеса 20см.
. Найти угловую и линейную скорость колеса, а также полное ускорение точек, лежащих на ободе колеса в конце первой секунды вращения. Радиус колеса 20см. 0 см =
0 см =  м;
м; с.
с.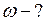
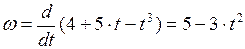 ;
; 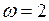 рад/с.
рад/с. м/с
м/с ;
;  рад/с2.
рад/с2. ;
;  м/с2.
м/с2.


