
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Две основные задачи динамики точки.Содержание книги
Поиск на нашем сайте
Две основные задачи динамики точки. 1. Зная массу материальной точки и уравнение ее движения определить модуль и направление равнодействующей силы, под действием которой точка движется. 2. Зная силы, действующие на материальную точку, ее массу и начальные условия движения определить траекторию. Дифференциальные уравнения движения свободной материальной точки в декартовых координатах. Метод кинетостатики: если к движущейся под действием сил точке приложить силу инерции, то геометрическая сумма всех сил будет равна нулю: Так как: Динамическая теорема Кориолиса. Переносная и Кориолисова силы инерции. Переносная сила инерции точки в ее относительном движении направлена противоположно вектору переносного ускорения точки и численно ровно произведению массы точки, на величину переносного ускорения точки: -maе=Фе - сила инерции Сила инерции Кориолиса, направлена в сторону противоположную ускорению Кориолиса, и ровно произведению массы точки на величину ускорения Кориолиса: -mak=Фk – Кориолисова сила инерции. mar=
Дифференциальные уравнения относительного движения материальной точки.
Свободные колебания материальной точки
x=x0coskt+ x=asin(kt+α) – 2-я форма уравнения гармонич. колебаний k= T= a=
Затухающие колебания мат. точки Затухающие колебания происходят в том случае, когда на точку, кроме восстанавливающей силы действует сила сопротивления. R=-µv µ - коэффициент сопротивления среды
n=
Затухающие колебания в случае малого сопротивления k k1=
Т= Д=-
Затухающие колебания в случае большого сопротивления n k1=
Вынужденные колебания без учета сопротивления среды Такие колебания происходят, если на точку, кроме восстанавливающей силы действует вынуждающая сила, изменяющаяся по гармоническому закону:
A=
Случай резонанса k=p
Вынужденные колебания с учетом сопротивления среды Такие колебания происходят, если на точку, кроме восстанавливающей и вынуждающей силы действует сила сопротивления: R=-µv µ - коэффициент сопротивления среды
13. Координаты центра масс системы материальных точек.Силы, действующие на точки механической системы. Механическая система материальных точек - совокупность точек, в которой положение и движение каждой зависит от остальных. Система с кинематическими ограничениями - несвободная. Масса механической системы - арифметическая сумма масс всех ее точек. Центр масс - геометрическая точка, положение которой определяется уравнениями: Внешние силы - силы, с которыми на механическую систему действуют другие тела, не входящие в нее. Внутренние силы - силы взаимодействия точек системы. Свойства внутренних сил: 1. главный вектор внутренних сил равен нулю; 2. главный вектор момент внутренних сил относительно любого неподвижного центра равен нулю
Теорема о моменте инерции относительно параллельных осей. Теорема: Момент инерции относительно оси равен сумме момента инерции относительно параллельной ей центральной оси и произведение массы тела на квадрат расстояния меду осями: Iz = Izc + mh2. Радиус инерции. Радиус инерции - расстояние от оси до воображаемой точки, в которой необходимо сосредоточить массу тела, чтоб момент инерции этой точки относительно заданной оси был равен моменту инерции данного тела относительно этой же оси: Работа. Работа силы - количественная мера превращения механического движения в другие виды движения. Если сила постоянна по модулю и направлению, а точка ее приложения перемещается прямолинейно, то работа равна произведению модуля силы, длинны перемещения и косинуса угла между этими векторами: Мощность - работа, выполненная за единицу времени. Теорема о работе равнодействующей силы: работа равнодействующей на некотором перемещении равна алгебраической сумме работ, составляющих ее сил на этом же перемещении. Явление удара. Явление, при котором, за ничтожно малые промежутки времени скорости точек тела изменяются на конечную величину, называется ударом. Силы, которые изменяют скорости точек в течении малого промежутка времени называются мгновенными или ударными. Фаза изменения скоростей – фаза деформации τ1 – время фазы деформации Sд= τ2 – время фазы восстановления Sв= Коэффициент восстановления при ударе K= u – скорость после удара v – скорость до удара Если К=0, то u=0 – абсолютно неупругий удар Если К=1, то u=v – абсолютно упругий удар Если
Теоремы теории удара -Теорема об изменении количества движения при ударе (Изменение количества движения системы за время удара, равно сумме всех внешних ударных импульсов действующих на систему: Q-Qi= -Теорема об изменении кинетического момента при ударе (Изменение за время удара кинетического момента системы относительно центра, ровно сумме моментов всех действующих на систему ударных импульсов: L-L0= -Теорема об изменении кинетической энергии при ударе (Т. Карно) (Кинетическая энергия потерянная системой, при абсолютно неупругом ударе, равна той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями: T-T0=
Две основные задачи динамики точки. 1. Зная массу материальной точки и уравнение ее движения определить модуль и направление равнодействующей силы, под действием которой точка движется. 2. Зная силы, действующие на материальную точку, ее массу и начальные условия движения определить траекторию.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.11.13 (0.006 с.) |

 , где Ф - сила инерции.
, где Ф - сила инерции. , то проектируя на ось координат получаю:
, то проектируя на ось координат получаю:  , так как:
, так как:  то аналогично для y и z получаю:
то аналогично для y и z получаю: 
 - динамическая теорема Кориолиса
- динамическая теорема Кориолиса , подставляя в основное уравнение динамики:
, подставляя в основное уравнение динамики:  , обозначая переносную и Кориолисову силы инерции:
, обозначая переносную и Кориолисову силы инерции:  . В проекциях на координатные оси:
. В проекциях на координатные оси: 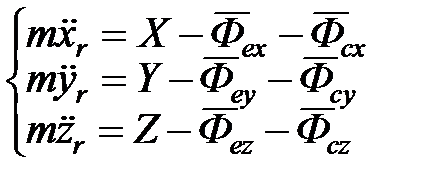
 - диф. уравнение свободных гармонич. колебаний
- диф. уравнение свободных гармонич. колебаний sinkt – 1-я форма уравнения гармонич. колебаний
sinkt – 1-я форма уравнения гармонич. колебаний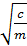 – круговая частота колебаний
– круговая частота колебаний – период
– период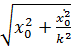 – амплитуда колебаний
– амплитуда колебаний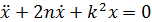 – диф. уравнение затухающих колебаний
– диф. уравнение затухающих колебаний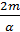 - частота затухающих колебаний
- частота затухающих колебаний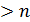
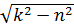 - частота
- частота - 1- я форма ур. зат. колебаний
- 1- я форма ур. зат. колебаний 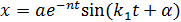 - 2- я форма ур. зат. колебаний
- 2- я форма ур. зат. колебаний – период
– период
 логарифмический дикримент затухания
логарифмический дикримент затухания
 - частота
- частота – ур-е затух. колебаний большого сопрот.
– ур-е затух. колебаний большого сопрот. случай апериодического движения
случай апериодического движения H
H диф. ур-е. вынужд. колеб. без сопр. сред
диф. ур-е. вынужд. колеб. без сопр. сред 1-я форма ур-я.
1-я форма ур-я. 2-я форма ур-я.
2-я форма ур-я. удельная амплитуда
удельная амплитуда амплитуда вынужденных колебаний
амплитуда вынужденных колебаний ур-е. колеб. р.
ур-е. колеб. р.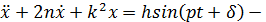 диф. ур-е. вынужд. колеб. с сопр. среды
диф. ур-е. вынужд. колеб. с сопр. среды - амплитуда вынужденных колебаний с сопр.
- амплитуда вынужденных колебаний с сопр. - ур-е вынужденных колеб.
- ур-е вынужденных колеб. Задаваемые силы и реакции связи;
Задаваемые силы и реакции связи; Ц ентробежный момент инерции:
Ц ентробежный момент инерции:  .
. . Знак работы совпадает со знаком проекции силы на ось перемещения.
. Знак работы совпадает со знаком проекции силы на ось перемещения. 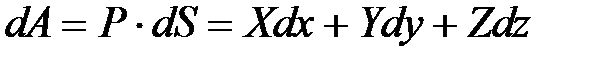 . Интегрируя для точки М получим:
. Интегрируя для точки М получим: 



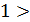 К
К  – упругий удар
– упругий удар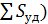
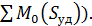
 ).
).


