
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава II. 5 всемирное тяготение. Элементы теории поляСодержание книги
Поиск на нашем сайте II.5.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ 1. Закон всемирного тяготения
где
Два шара со сферически симметричным распределением плотности вещества в каждом шаре притягивают друг друга так, как будто вся масса каждого шара сосредоточена в его центре. 2. Напряжённость гравитационного поля
где Если гравитационное поле, напряжённость которого мы определяем, само создано материальной точкой или телом со сферически симметричным распределением плотности, то
где
3. Ускорение свободного падения
где Если
4. Потенциальная энергия гравитационного взаимодействия двух материальных точек всегда отрицательна и выражается формулой
где При 5. Работа сил гравитационного поля при сближении двухматериальных точек равна уменьшению потенциальной энергии тяготения
Работа сил гравитационного поля при сближении двухвзаимодействующих материальных точек положительна и выражается формулой
где Если расстояние между материальными точками увеличивается, то работа сил поля отрицательна. Работа сил гравитационного поля при перемещении материальной точки массой
6. Потенциал гравитационного поля
где Потенциал гравитационного поля можно выразить и через работу сил тяготения
Работа в данном случае отрицательна. Если поле создано материальной точкой или телом со сферически симметричным распределением плотности, то
где 7. Связь между потенциалом поля тяготения и его напряжённостью
8. Если какое-либо тело движется в поле тяготения Земли (или другого небесного тела), то полная механическая энергия
или
где
9. Законы Кеплера § Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце. § Радиус – вектор планеты в равные времена описывают площади одинаковой величины. § Квадраты периодов обращения любых двух планет относятся как кубы больших полуосей их орбит
Законы Кеплера справедливы также для движения спутников вокруг планет. 10. Первая и вторая космические скорости
где 11. Основной закон динамики для неинерциальных систем отсчёта
где
12. Силы инерции
где
II.5.2 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ЗАДАЧА № II.78 Барон Мюнхгаузен, герой известного произведения Э. Распе, привязав конец веревки к Луне, спускался по ней на Землю. Объясните с точки зрения физики невозможность такого передвижения. Ответ. Барон Мюнхгаузен никак не мог бы скользить по веревке к Земле, так как этому препятствовала бы сила притяжения его к Луне.
ЗАДАЧА № II.79 На динамометре подвешен груз. Изменятся ли показания прибора, если его поднять на большую высоту над поверхностью Земли? Ответ. Показания прибора уменьшатся, так как сила тяжести обратно пропорциональна расстоянию от тела до поверхности Земли.
ЗАДАЧА № II.80 Почему сила тяжести зависит от широты местности? В каком случае сила тяжести в разных точках на поверхности Земли была бы одинаковой? Зависит ли масса тела от широты местности? Ответ. Так как Земля сплюснута у полюсов, то сила тяжести, зависящая от расстояния до центра Земли, будет разной на разных широтах. Масса тела не зависит от широты места.
ЗАДАЧА № II.81 Аристотель утверждал, что если на кирпич, который падает с определенной скоростью, положить сверху другой кирпич, то верхний будет давить на нижний, и поэтому два кирпича должны падать быстрее, чем один. Согласны ли вы с этим рассуждением Аристотеля? Ответ. Оба кирпича будут падать с одинаковой скоростью, поэтому дополнительного давления верхнего кирпича на нижний не будет.
ЗАДАЧА № II.82 Представим себе, что вокруг Земли построили мост из однородного материала. Вес тела в любой части моста один и тот же. Обрушится ли мост, когда из-под него удалят все опоры? Можно ли будет им воспользоваться для практических целей? Ответ. Мост должен держаться без опор, так как все его части притягиваются к центру Земли с одинаковой силой. Однако им пользоваться нельзя, так как достаточно даже небольшой мухе сесть на какую-нибудь часть моста, как нарушится равновесие, и мост рухнет.
ЗАДАЧА № II.83 С одной и той же высоты начинают одновременно падать монета и такой же по размеру кружок бумаги. Одновременно ли они упадут на поверхность Земли? Как изменится результат эксперимента, если бумажный кружок положить на монету и их отпустить? Ответ. Воздух оказывает большее сопротивление падающему кружку бумаги, чем монете. Поэтому монета окажется на поверхности Земли раньше. Если бумажный кружок положить на монету, то они будут падать как единое целое с одинаковым ускорением, поэтому окажутся на поверхности Земли одновременно.
ЗАДАЧА № II.84 Из ружья произведен одиночный выстрел. Что раньше упадет на поверхность Земли: стреляная гильза или пуля, если считать, что они вылетают одновременно в горизонтальном направлении? Сопротивление воздуха не учитывайте. Ответ. Гильза и пуля упадут одновременно.
ЗАДАЧА № II.85 Если спортсмен перед прыжком делает разбег, то дальность прыжка увеличивается. Почему? В каком состоянии находится спортсмен во время полета? Ответ. Разбег увеличивает горизонтальную составляющую скорости прыжка, поэтому увеличивается дальность полета. При этом спортсмен находится в состоянии свободного падения.
ЗАДАЧА № II.86 Известно, что в вакууме время подъема тела, брошенного вертикально вверх, равно времени его падения. Будет ли иметь место это равенство, если учитывать сопротивление воздуха? Ответ. Время подъема будет меньше времени падения. При подъеме камня сила тяжести, действующая на него, направлена так же, как и сила сопротивления воздуха, а при падении — противоположно.
ЗАДАЧА № II.87 Может ли космонавт ходить в условиях невесомости, например, по полу или стене орбитальной станции, не пользуясь поручнями? Ответ. В состоянии невесомости отсутствует сила давления человека на пол (стенки) станции, поэтому не возникает сила трения, необходимая для ходьбы.
ЗАДАЧА № II.88 Определитесреднюю плотность Земли, считая известными гравитационную постоянную, радиус Земли и ускорение свободного падения на Земле.
Дано:
Найти: Решение
Среднюю плотность Земли
где Так как масса по условию задачи нам не известна, то её можно будет выразить из закона Всемирного тяготения:
где На основании второго закона Ньютона: Выразим из последнего равенства массу Земли, получим:
Объём Земли, определим по формуле:
Подставим формулы (3) и (4) в формулу (1), получим:
ЗАДАЧА № II.89 Как известно, искусственный спутник Земли движется вокруг неё по круговой орбите. Определите, во сколько раз гравитационная потенциальная энергия спутника больше его кинетической энергии. Дано: Найти: Решение
Потенциальная энергия гравитационного взаимодействия искусственного спутника и Земли выражается формулой:
Кинетическая энергия спутника может быть определена по формуле:
Определим, во сколько раз гравитационная потенциальная энергия спутника больше его кинетической энергии:
Искусственный спутник Земли движется вокруг неё по круговой орбите, следовательно, на основании второго закона Ньютона:
Из формулы (4) видно, Подставим данное выражение в формулу (3), получим:
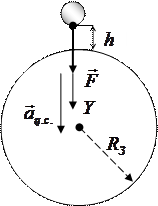
ЗАДАЧА № II.90 Вычислить ускорение свободного падения тела, находящегося на расстоянии 100 км от поверхности Земли.
Дано: Найти: Решение
На тело, находящееся на высоте
где Под действием этой силы тело будет двигаться вертикально вниз равноускоренно с ускорением
Запишем для тела уравнение второго закона Ньютона в скалярной форме относительно оси
Приравняем формулы (1) и (2), получим:
Выразим из формулы (3), ускорение свободного падения:
В формуле (4):
У поверхности Земли
После почленного деления уравнений (5) и (6), получим:
Выразим из формулы (7) ускорение свободного падения
Так как
ЗАДАЧА № II.91 Подлетев к неизвестной планете, космонавты придали своему кораблю горизонтальную скорость 11 км/с. Эта скорость обеспечила полёт корабля по круговой орбите радиусом 9100 км. Каково ускорение свободного падения у поверхности планеты, если её радиус 8900 км? Дано:
Найти: Решение
На космический корабль действуют только одна сила тяготения со стороны планеты, направленная к её центру (рис.75) и согласно закону всемирного тяготения равная:
где
Преобразуем выражение (1), умножив числитель и знаменатель на
Здесь, как и в случае Земли,
Запишем для космического корабля уравнение второго закона Ньютона в скалярной форме относительно оси
где
Подставим выражения (1) и (3) в формулу (2) и выразим из неё ускорение
ЗАДАЧА № II.92 Средняя высота спутника над поверхностью Земли 1700 км. Определить его скорость и период вращения. Дано: Найти: Решение
Движение по круговой орбите происходит под действием только силы тяготения со стороны Земли:
где Запишем для спутника уравнение второго закона Ньютона в скалярной форме относительно оси
где
Учитывая формулы (1) и (3), преобразуем уравнение (2) и выразим из него скорость движения спутника:
Умножая числитель и знаменатель правой части уравнения (4) на
откуда
Период вращения спутника по круговой орбите радиусом
где
Подставим выражение (8), в формулу (7), получим:
ЗАДАЧА № II.93 Найти первую космическую скорость Дано:
Найти: Решение
На тело, движущееся по круговой орбите вокруг Земли, действует единственная сила – сила тяготения. Эта сила и определяет центростремительное ускорение спутника (рис. 76). Итак,
где
Для удобства расчёта воспользуемся формулой:
Перепишем формулу (3) в виде:
Заметим, что все тела внутри спутника будут находиться в состоянии невесомости, так как они движутся с одинаковым ускорением, которое создаётся только силой тяготения. Сила нормальной реакции ЗАДАЧА № II.94 Радиус орбиты Нептуна в 30 раз больше радиуса орбиты Земли. Определить продолжительность года на Нептуне, предварительно показав, что квадраты периодов вращения планет вокруг Солнца относятся как кубы радиусов орбит их вращения. Дано:
Найти: Решение
Покажем, что квадраты периодов вращения планет вокруг Солнца относятся как кубы радиусов орбит их вращения. Для этого сначала запишем формулу, по которой находится период вращения:
Для нахождения скорости
где
Движение по круговой орбите происходит под действием только силы тяготения со стороны Земли:
где Подставим формулы (3) и (4) в (2), получим:
Выразим из равенства (5), скорость
Аналогично, найдём период вращения
В формулах (6) и (7) периоды:
Выразим продолжительность года на Нептуне
ЗАДАЧА № II.95 Наэкваторе воображаемой планеты,имеющей форму шара, тела весят вдвое меньше, чем на полюсах. Найти среднюю плотность вещества планеты, если период вращения вокруг оси 1ч 27,2 мин.
Дано:
Найти: Решение
На полюсе, согласно второго закона Ньютона (в скалярной форме) (рис.77):
где
Подставим формулы (4), (3) и (2) в формулу (1), получим:
Применительно к экватору, второй закон Ньютона в скалярной форме будет иметь вид:
где
Выразим из формулы (6)
где
Решая совместно уравнения (9), (8) и (5) и учитывая, что
ЗАДАЧА № II.96 Найти центробежную силу инерции, действующую на экваторе на тело массой 100 кг. Радиус Земли равен
Дано:
Найти: Решение
Центробежная сила инерции определяется по формуле:
где Угловую скорость вращения Земли, можно определить по формуле:
где Подставим формулу (2) в формулу (1), получим:
ЗАДАЧА № II.97 Пластинка радиусом 20 см равномерно вращается в горизонтальной плоскости, совершая 33 оборота в минуту. От точки Дано:
Найти: Решение
Во вращающейся системе на жучка действуют сила Кориолиса
где Центробежная сила
Сила трения будет равна:
Сравнивая (1), (2) и (3) можно заключить, что самый критический момент соответствует краю пластинки. Угол Равнодействующую сил
Отсюда
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 993; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

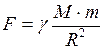 , (II.76)
, (II.76)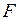 - сила взаимного притяжения двух тел, размерами которых можно пренебречь по сравнению с расстоянием между ними;
- сила взаимного притяжения двух тел, размерами которых можно пренебречь по сравнению с расстоянием между ними;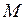 и
и 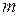 - массы тел;
- массы тел; 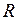 - расстояние между ними;
- расстояние между ними; - гравитационная постоянная.
- гравитационная постоянная. , (II.77)
, (II.77)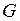 =
= 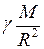 , (II.78)
, (II.78)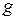 на высоте
на высоте  над поверхностью Земли
над поверхностью Земли , (II.79)
, (II.79)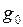 - ускорение на поверхности Земли.
- ускорение на поверхности Земли.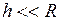 , то
, то . (II.80)
. (II.80)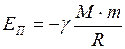 , (II.81)
, (II.81)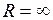 потенциальная энергия системы имеет максимальное значение, равное нулю.
потенциальная энергия системы имеет максимальное значение, равное нулю. . (II.82)
. (II.82)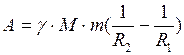 , (II.83)
, (II.83)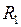 и
и 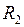 - соответственно начальное и конечное расстояния между материальными точками (
- соответственно начальное и конечное расстояния между материальными точками (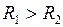 ).
).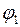 в точку с потенциалом
в точку с потенциалом 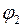 :
: . (II.84)
. (II.84)
 , (II.85)
, (II.85)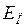 - потенциальная энергия материальной точки массой
- потенциальная энергия материальной точки массой  , совершаемую при перемещении материальной точки массой
, совершаемую при перемещении материальной точки массой 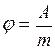 . (II.86)
. (II.86)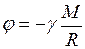 , (II.87)
, (II.87) . (II.88)
. (II.88)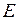 тела равна сумме его кинетической и потенциальной энергии
тела равна сумме его кинетической и потенциальной энергии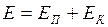 (II.89)
(II.89)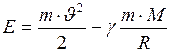 , (II.90)
, (II.90)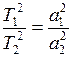 . (II.91)
. (II.91)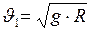 ;
; 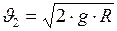 , (II.92)
, (II.92) , (II.93)
, (II.93)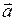 и
и  - соответственно ускорение тела в инерциальной и неинерциальной системах отсчёта;
- соответственно ускорение тела в инерциальной и неинерциальной системах отсчёта; - силы инерции.
- силы инерции. , (II.94)
, (II.94) - силы инерции, проявляющиеся при поступательном движении системы отсчёта с ускорением
- силы инерции, проявляющиеся при поступательном движении системы отсчёта с ускорением 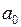 :
: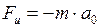 ; (II.95)
; (II.95)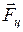 - центробежные силы инерции (силы инерции, действующие во вращающейся системе отсчёта на тела, удалённые от оси вращения на конечное расстояние
- центробежные силы инерции (силы инерции, действующие во вращающейся системе отсчёта на тела, удалённые от оси вращения на конечное расстояние  . (II.96)
. (II.96)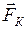 - кориолисова сила инерции (силы инерции, действующие на тело, движущееся со скоростью
- кориолисова сила инерции (силы инерции, действующие на тело, движущееся со скоростью 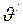 во вращающейся системе отсчёта):
во вращающейся системе отсчёта):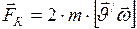 . (II.97)
. (II.97)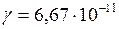 м3/(кг∙с2);
м3/(кг∙с2); м;
м; м/с2.
м/с2.
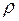 можно будет найти, используя формулу:
можно будет найти, используя формулу: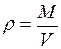 , (1)
, (1)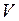 - объём Земли.
- объём Земли. , тогда
, тогда  .
.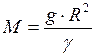 . (3)
. (3) . (4)
. (4)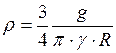 ;
;  кг/м3.
кг/м3.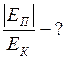
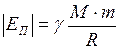 . (1)
. (1) . (2)
. (2)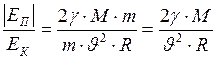 . (3)
. (3) . (4)
. (4)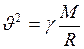 .
.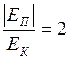 .
.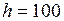 км
км  м
м
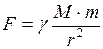 , (1)
, (1)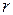 - расстояние от центра Земли до тела.
- расстояние от центра Земли до тела.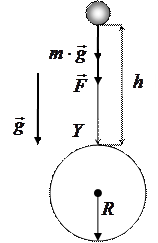
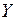 , направленной вертикально вниз:
, направленной вертикально вниз: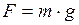 . (2)
. (2)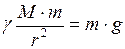 . (3)
. (3) , (4)
, (4) , где
, где 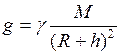 . (5)
. (5)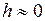 , поэтому
, поэтому  и
и 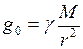 ; (6)
; (6)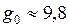 м/с2.
м/с2.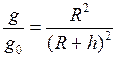 . (7)
. (7) . (8)
. (8) , то воспользуемся приближённым соотношением
, то воспользуемся приближённым соотношением 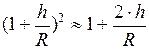 . Тогда с учётом этого, уравнение (7), перепишется в виде:
. Тогда с учётом этого, уравнение (7), перепишется в виде: ;
; 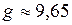 м/с2.
м/с2.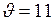 км/с
км/с  м/с;
м/с;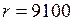 км
км  м;
м; км
км  м.
м.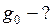
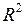 , получим:
, получим: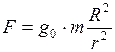 . (2)
. (2) - ускорение свободного падения у поверхности планеты.
- ускорение свободного падения у поверхности планеты.
 , (2)
, (2) . (3)
. (3) ;
; 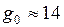 м/с2.
м/с2.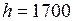 км
км 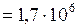 м
м

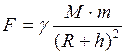 , (1)
, (1)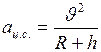 . (3)
. (3)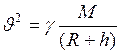 . (4)
. (4)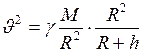 , где
, где 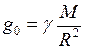 ускорение свободного падения у поверхности Земли. Следовательно,
ускорение свободного падения у поверхности Земли. Следовательно, , (5)
, (5) ; (6)
; (6) м/с.
м/с.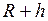 , найдём по формуле:
, найдём по формуле: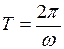 , (7)
, (7) - угловая скорость, в условиях данной задачи, она будет определена с.о.:
- угловая скорость, в условиях данной задачи, она будет определена с.о.: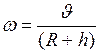 . (8)
. (8)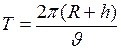 ;
; 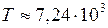 с.
с.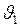 . Первая космическая скорость – скорость, которую надо сообщить телу, чтобы оно стало спутником Земли.
. Первая космическая скорость – скорость, которую надо сообщить телу, чтобы оно стало спутником Земли. км
км 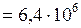 м;
м; м/с2.
м/с2.
 , (1)
, (1)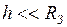 . Тогда
. Тогда . (2)
. (2) . (3)
. (3)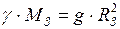 и подставим её в формулу (2), получим:
и подставим её в формулу (2), получим: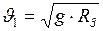 ;
; 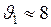 км/с.
км/с. , следовательно, равен нулю и вес тела.
, следовательно, равен нулю и вес тела.

 . (1)
. (1) . (3)
. (3)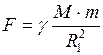 , (4)
, (4)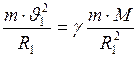 . (5)
. (5)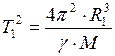 . (6)
. (6)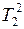 :
: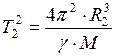 . (7)
. (7) и
и  соответствуют продолжительности года на Земле и Нептуне:
соответствуют продолжительности года на Земле и Нептуне:  и
и  , а радиусы
, а радиусы  и
и 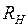 . С учётом этого и поделив почлено (6) на (7), получим следующее отношение:
. С учётом этого и поделив почлено (6) на (7), получим следующее отношение: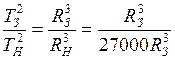 . (8)
. (8)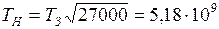 с.
с.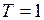 ч
ч 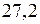 мин.
мин.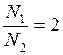

 . (1)
. (1) . (4)
. (4)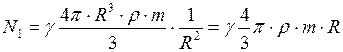 . (5)
. (5)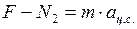 , (6)
, (6)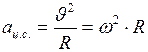 . (7)
. (7)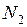 и подставим формулу (7), получим:
и подставим формулу (7), получим: . (8)
. (8)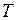 :
: . (9)
. (9) ;
; 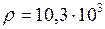 кг/м3.
кг/м3.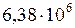 м.
м. кг;
кг;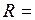

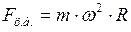 , (1)
, (1)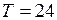 ч.
ч. 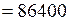 с).
с).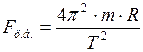 ;
;  Н.
Н. (об/мин)
(об/мин)  об/с;
об/с;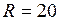 см
см 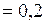 м;
м;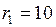 см
см 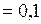 м;
м; (см/с)
(см/с) 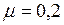
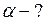

 и центробежная сила
и центробежная сила 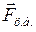 . Равнодействующая этих сил
. Равнодействующая этих сил  должна уравновешиваться силой трения. Найдём эти силы.
должна уравновешиваться силой трения. Найдём эти силы.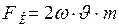 ;
; 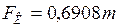 (1)
(1)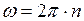 - угловая скорость;
- угловая скорость;  . (2)
. (2)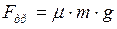 ;
;  . (3)
. (3)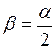 ,
, 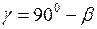 ,
,  ,
,  .
.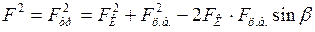 . (4)
. (4) ;
; 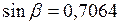
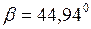 ;
; 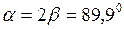 .
.


