
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. 1. 5 равнопеременное прямолинейное ДвижениеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Равнопеременное прямолинейное движение является частным случаем неравномерного движения, ускорение при котором остаётся постоянным как по модулю, так и по направлению ( Среднее ускорение Если направление ускорения Если направление векторов ускорения Изменение скорости На графике это можно будет представить следующим образом (рис.11).
На данном графике ускорение характеризуется тангенсом угла между касательной к скорости и осью времени: Если в начальный момент времени
Проекция вектора скорости на ось
Аналогично записываются уравнения для проекций вектора скорости на другие координатные оси. Формулы (I.13) и (I.13/) выражают алгебраическую зависимость скорости от времени и представляют собой первый закон равнопеременного движения. Та же зависимость может быть наглядно представлена графически (рис.12). Будем откладывать на оси абсцисс время
Второй закон равнопеременного движения - устанавливает связь между пройденным расстоянием и временем движения (т.е. даёт уравнение этого движения). Получим его графическим методом, используя рисунок 12. Для этого разобьём площадь
При
График зависимости
При прямолинейном равнозамедленном движении формула пути:
Окончательно два закона равнопеременного движения будут выглядеть следующим образом:
Из этих двух законов вытекают некоторые соотношения, имеющие частое применение в задачах и технике. 1. Для равноускоренного движения без начальной скорости (как уже говорилось выше) эти законы упрощаются:
2. Исключая время
при
3. Обозначим через
Расстояния, проходимые в последовательные единицы времени, относятся, как ряд нечётных чисел. Осталось рассмотреть графики зависимости ускорения от времени при равноускоренном и равнозамедленном движениях. График График
а)
I.1.6 СВОБОДНОЕ ПАДЕНИЕ ТЕЛ Падение тел происходит по законам равнопеременного движения; это было установлено Галилеем при движении шарика по наклонной плоскости и может быть продемонстрировано при помощи машины Атвуда и многих других приборов, которые имеют целью замедлить движение и сделать явление падения легко наблюдаемым. Свободным падением называется движение, которое совершало бы тело только под действием силы тяжести без учёта сопротивления воздуха. При свободном падении тела с небольшой высоты Ускорение Величина нормального ускорения свободного падения (т.е. на уровне моря на Законы движения падающего тела, вследствие постоянства
где Применим их к некоторым частным случаям. 1. Свободное падение с высоты
Скорость, с которой падающее тело достигает поверхности Земли, определяется по формуле:
2. Движение тела, брошенного вертикально вверх (рис.16,а). Тело, брошенное вертикально вверх, движется равнозамедленно с начальной скоростью
Движение тела, брошенного вертикально вниз (рис.16,б), представляет собой равноускоренное движение с ускорением Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в нуль:
А из формулы (I.26) найдём время подъёма тела на максимальную высоту:
3. Движение тела, брошенного горизонтально. Движение тела, брошенного горизонтально, представляет собой комбинацию двух движений, взаимно перпендикулярных друг другу: q горизонтального (равномерного) движения; q вертикального (свободного падения). Если построить траекторию движения тела, брошенного горизонтально, в системе координат
Подставив
Так как
Положение каждой точки траектории можно задать вектором положения
Вектор мгновенной скорости
Модуль вектора (I.33) запишется как:
4. Движение тела, брошенного под углом к горизонту. Движение тела, брошенного под углом к горизонту, представляет собой комбинацию двух поступательных движений: q свободного падения в вертикальном направлении; q равномерного прямолинейного движения под углом
На рисунке 19 представлена траектория движения тела, брошенного под углом к горизонту. Перемещение тела к моменту времени
В наивысшей точке
Для нахождения общего времени движения, рассмотрим точку
Максимальная высота подъёма определится по формуле:
Дальность броска определяется по формуле (I.35):
На что необходимо обратить внимание: q Сопротивление воздуха не учитывалось. q При постоянной начальной скорости дальность броска зависит от угла.
Из формулы (I.40) следует, что она максимальна при
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.119 (0.011 с.) |

 .
. будет равно мгновенному ускорению
будет равно мгновенному ускорению 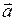 . Направлено ускорение
. Направлено ускорение 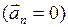 .
. то, движение называется равноускоренным. Модуль скорости равноускоренного движения точки с течением времени возрастает.
то, движение называется равноускоренным. Модуль скорости равноускоренного движения точки с течением времени возрастает.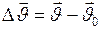 в течение промежутка времени
в течение промежутка времени  при равнопеременном прямолинейном движении равно:
при равнопеременном прямолинейном движении равно:  , или
, или 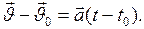

 .
. скорость точки равна
скорость точки равна 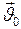 (начальная скорость) и ускорение
(начальная скорость) и ускорение  :
: . (I.13)
. (I.13) прямоугольной декартовой системы координат связана с соответствующими проекциями векторов начальной скорости и ускорения уравнением:
прямоугольной декартовой системы координат связана с соответствующими проекциями векторов начальной скорости и ускорения уравнением: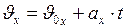 . (I.13/)
. (I.13/) в соответствующие моменты времени; к первоначальной скорости
в соответствующие моменты времени; к первоначальной скорости  каждую секунду, прибавляется приращение
каждую секунду, прибавляется приращение  .
.
 на узкие полоски
на узкие полоски  и примем площадь каждой из них за площадь прямоугольника; она и выразит путь, пройденный материальной точкой за малый промежуток времени
и примем площадь каждой из них за площадь прямоугольника; она и выразит путь, пройденный материальной точкой за малый промежуток времени  , в течение которого скорость можем принимать постоянной. Составив сумму таких площадей, определим путь, пройденный за время движения
, в течение которого скорость можем принимать постоянной. Составив сумму таких площадей, определим путь, пройденный за время движения 
 от
от 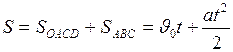 . Эта формула устанавливает искомую зависимость пройденного при равнопеременном движении расстояния от времени (второй закон равнопеременного движения):
. Эта формула устанавливает искомую зависимость пройденного при равнопеременном движении расстояния от времени (второй закон равнопеременного движения): . (I.14)
. (I.14) путь равен:
путь равен: . (I.15)
. (I.15) для равноускоренного движения изображён на рисунке 13.
для равноускоренного движения изображён на рисунке 13.
 . (I.16)
. (I.16) График зависимости
График зависимости  (I.17)
(I.17)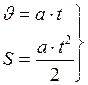 (I.18)
(I.18) . (I.19)
. (I.19) . (I.20)
. (I.20) расстояния, проходимые в одну, две, три,…секунды; имеем:
расстояния, проходимые в одну, две, три,…секунды; имеем: ;
; 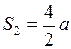 ;
;  ;
;  ;…;
;…; ;
;  ;
; 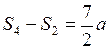 ;…;
;…;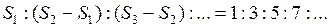
 при равноускоренном движении представляет собой линию, параллельную оси времени и расположенную выше этой оси (рис.15,а).
при равноускоренном движении представляет собой линию, параллельную оси времени и расположенную выше этой оси (рис.15,а). б)
б) от поверхности Земли (
от поверхности Земли (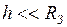 , где
, где  - радиус Земли) оно движется с постоянным ускорением
- радиус Земли) оно движется с постоянным ускорением  , направленным по вертикали вниз.
, направленным по вертикали вниз. северной широты) составляет
северной широты) составляет  м/с2. На полюсах ускорение свободного падения больше (
м/с2. На полюсах ускорение свободного падения больше ( м/с2), а на экваторе меньше (
м/с2), а на экваторе меньше ( м/с2). Это обусловлено суточным вращением Земли вокруг своей оси, с одной стороны, и сплюснутостью Земли – с другой (экваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Различие значений
м/с2). Это обусловлено суточным вращением Земли вокруг своей оси, с одной стороны, и сплюснутостью Земли – с другой (экваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Различие значений 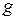 невелико, поэтому ускорение свободного падения, которое используется при решении практических задач, принимается равным 9,81 м/с2.
невелико, поэтому ускорение свободного падения, которое используется при решении практических задач, принимается равным 9,81 м/с2. ; (I.21)
; (I.21) , (I.22)
, (I.22) ;
;  . (I.23)
. (I.23) . (I.24)
. (I.24) . Для описания этого движения, используют следующие формулы:
. Для описания этого движения, используют следующие формулы: . (I.25)
. (I.25)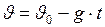 . (I.26)
. (I.26) . (I.27)
. (I.27) . Для его описания можно воспользоваться формулами (I.25) - (I.27), поменяв в них знак «-» на «+».
. Для его описания можно воспользоваться формулами (I.25) - (I.27), поменяв в них знак «-» на «+». . (I.28)
. (I.28) . (I.29)
. (I.29)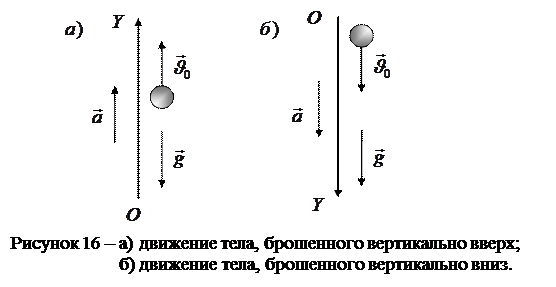
 , то координаты каждой точки
, то координаты каждой точки  траектории представляют собой перемещения тела в горизонтальном направлении (движение с постоянной скоростью
траектории представляют собой перемещения тела в горизонтальном направлении (движение с постоянной скоростью  ;
;  . (I.30)
. (I.30)
 во второе уравнение (I.30), получим уравнение траектории тела, брошенного горизонтально:
во второе уравнение (I.30), получим уравнение траектории тела, брошенного горизонтально: . (I.31)
. (I.31)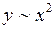 , т.е. траектория движения представляет собой параболу.
, т.е. траектория движения представляет собой параболу.
 (рис.17), который представляет собой результирующее перемещение:
(рис.17), который представляет собой результирующее перемещение:  , или
, или (I.32)
(I.32)
 в каждой точке траектории является результирующей мгновенных скоростей этих движений (рис.18):
в каждой точке траектории является результирующей мгновенных скоростей этих движений (рис.18): . (I.33)
. (I.33) . (I.34)
. (I.34) к горизонту.
к горизонту.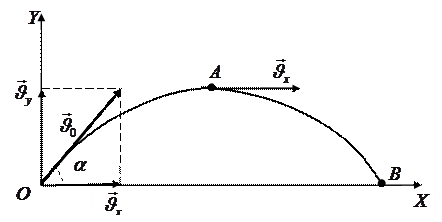
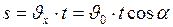 , (I.35)
, (I.35) . (I.36)
. (I.36) . Тогда уравнение (I.26) для скорости будет иметь вид:
. Тогда уравнение (I.26) для скорости будет иметь вид:  , где
, где  -время подъёма на максимальную величину:
-время подъёма на максимальную величину: . (I.37)
. (I.37) . В этой точке:
. В этой точке:  ;
;  . Тогда уравнение (I.25), перепишется в виде:
. Тогда уравнение (I.25), перепишется в виде: , где
, где  - общее время движения. Выразим его:
- общее время движения. Выразим его: . (I.38)
. (I.38) . Подставим сюда выражение (I.37), получим:
. Подставим сюда выражение (I.37), получим: . (I.39)
. (I.39) . Подставив выражение (I.38), получим:
. Подставив выражение (I.38), получим: . (I.40)
. (I.40) , так как
, так как  . При значениях
. При значениях 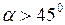 и
и 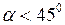 дальность броска будет меньше.
дальность броска будет меньше.


