
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика поступательного движенияСодержание книги
Поиск на нашем сайте
• Кинематические уравнения движения
• Средняя скорость
за время • Средняя путевая скорость
за время • Мгновенная скорость
• Проекции скорости
• Модуль скорости
• Мгновенное ускорение
• Проекции ускорения на оси координат х, у,z
• Модуль ускорения
• Ускорение при криволинейном движении (по дуге окружности)
по радиусу к центру окружности;
по касательной к точке окружности; • Модули ускорений
• Уравнения равномерного и равнопеременного движений
“+” - равноускоренное, “ - “ – равнозамедленное.
• Движение тела вертикально вверх
где
• Движение тела вертикально вниз
Кинематика вращательного движения
Положение твёрдого тела (при заданной оси вращения) задается углом поворота • Кинематическое уравнение вращательного движения
• Мгновенная угловая скорость
• Угловое ускорение
• Связь линейных характеристик с угловыми
• Уравнения равномерного и равнопеременного вращений
• Частота и период вращения: Частота (число оборотов в единицу времени) период (время одного полного оборота) циклическая (круговая)частота
Динамика Поступательного движения материальной точки Динамика – раздел механики, изучающий движение материальной точки (тела) с учетом сил, действующих на неё (него) со стороны других тел и полей.
• Уравнение движения (второй закон Ньютона)
• Импульс материальной точки (тела)
• Второй закон Ньютона с учетом импульса
• Второй закон Ньютона в скалярной форме
Виды сил • Сила гравитационного взаимодействия (закон всемирного тяготения)
где
• Ускорение свободного падения у поверхности планет
где M- масса планеты, R – радиус планеты. Ускорение свободного падения у поверхности Земли Ускорение свободного падения для тел, поднятых над Землей на высоту
• Сила тяжести
• Сила упругости (закон Гука)
где
• Сила реакции опоры - обозначается Если материальная точка находится на горизонтальной поверхности, то
• Сила трения скольжения
• Работа, совершаемая силой
где
• Мощность
• Кинетическая энергия материальной точки
• Потенциальная энергия материальной точки, находящейся в гравитационном поле Земли
• Потенциальная энергия сжатой (или растянутой) пружины
• Законы сохранения: Закон сохранения импульса Закон сохранения энергии • Законы сохранения для абсолютно упругого и неупругого ударов: Абсолютно упругий удар Закон сохранения импульса Закон сохранения энергии Абсолютно неупругий удар Закон сохранения импульса Закон сохранения энергии
Динамика
|
||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 129; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.49.90 (0.008 с.) |

 , где
, где  - время;
- время; , где
, где 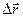 - перемещение материальной точки
- перемещение материальной точки ;
; , где
, где 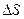 - путь, пройденный материальной точкой
- путь, пройденный материальной точкой , где
, где  - радиус вектор;
- радиус вектор; на оси координат х, у,z
на оси координат х, у,z ;
; ;
; , где
, где  ;
; ;
; ;
; , где
, где  - нормальное ускорение, направленное
- нормальное ускорение, направленное -тангенциальное ускорение, направленное
-тангенциальное ускорение, направленное ,
,  ,
,  ;
;  -радиус окружности;
-радиус окружности;
 - равномерное движение;
- равномерное движение;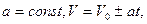
 - равнопеременное движение;
- равнопеременное движение; ,
, 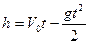 ,
, м/с
м/с  - ускорение свободного падения у поверхности Земли;
- ускорение свободного падения у поверхности Земли; - высота подъёма.
- высота подъёма. ,
,  .
. .
. ; (пример
; (пример  )
) ;
; ;
;

 ,
,  ;
;
 - равномерное вращение;
- равномерное вращение;
 - равнопеременное вращение;
- равнопеременное вращение; ,
, ,
, ,
,  ,
,  , где N – число оборотов.
, где N – число оборотов. =
=  , где
, где  - масса,
- масса, 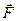 - сила.
- сила. , где
, где  ,
,  ;
;
 , где
, где  - изменение импульса;
- изменение импульса; - импульс силы.
- импульс силы. ,
,
 - гравитационная постоянная,
- гравитационная постоянная,  - расстояние между материальными точками.
- расстояние между материальными точками. ,
,
 .
. .
. ,
,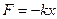 ,
,  ,
, - изменение размеров тела (удлинение),
- изменение размеров тела (удлинение),  - коэффициент упругости,
- коэффициент упругости, - напряжение в теле, возникающее за счет действия силы,
- напряжение в теле, возникающее за счет действия силы, 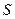 - площадь поперечного сечения тела,
- площадь поперечного сечения тела,  - относительное удлинение, Е – модуль Юнга (модуль упругости).
- относительное удлинение, Е – модуль Юнга (модуль упругости). .
. ;
; , где
, где  - коэффициент трения;
- коэффициент трения;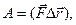
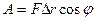 ,
, - перемещение материальной точки под действием силы,
- перемещение материальной точки под действием силы,  - средняя мощность;
- средняя мощность;  - мгновенная мощность;
- мгновенная мощность; - скорость движения.
- скорость движения. ,
,  ; где
; где  - импульс;
- импульс;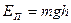 , где
, где  ; где
; где  для замкнутых систем.
для замкнутых систем. для замкнутых систем;
для замкнутых систем; ;
; ;
;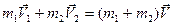 ;
; ;
;


