
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа 1-07 “Определение момента инерции тела с помощью наклонной плоскости”.Содержание книги
Поиск на нашем сайте
Цель работы: усвоение понятия момента инерции тела и определение момента инерции тел из закона сохранения энергии. Теоретическое введение Характеристики движения твердого тела, вращающегося вокруг неподвижной оси, могут быть определены из основного уравнения динамики вращательного движения
где Уравнение (7.1) – это второй закон Ньютона для вращательного движения. То есть, отличительной особенностью задачи о вращении тела вокруг оси по сравнению с задачей о движении материальной точки является то, что теперь в основное уравнение входит не масса тела При выводе этого уравнения пользуются приемом, который применяется в механике для изучения движения абсолютно твердых тел конечных размеров. Все тело мысленно разбивается на совокупность маленьких частичек с массами
Величина В случае непрерывного распределения масс с плотностью
Вычисление момента инерции твердого тела произвольной формы относительно оси представляет собой сложную задачу – необходимо знать, как плотность тела
Величины моментов инерции чаще определяют из опыта. Рассмотрим, как это можно сделать, решая задачу о скатывании круглого однородного тела радиусом Задача о скатывании – пример плоского движения твердого тела, т.е. движения, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Если ось вращения проведем через центр масс тела (т. О) перпендикулярно плоскостям, в которых лежат траектории точек тела, то она (эта ось) будет двигаться поступательно, оставаясь параллельной самой себе. В этом случае кинетическую энергию твердого тела при плоском движении можно представить как энергию вращения вокруг оси, проходящей через центр масс тела и энергию поступательного движения со скоростью, равной скорости центра масс
здесь Если тело скатывается с высоты
Рис. 7.1. Центр масс тела движется равноускоренно под действием силы трения покоя
где Предполагается, что тело скатывается без скольжения, и поэтому линейная скорость точек соприкосновения тела с наклонной плоскостью равна нулю, и так что скорость поступательного движения Если теперь подставить выражения для
Это соотношение позволяет, измерив на опыте время скатывания тела В то же время из (7.3) можно теоретически рассчитать момент инерции шара – цилиндра –
пустотелого цилиндра и сравнить их с измеренными значениями. При решении задачи о качении тела предполагали, что силами трения качения можно пренебречь. Поэтому в законе сохранения энергии не учитывали работу этих сил трения. Сила же трения покоя (рис.7.1) как раз и создает вращающий момент относительно оси, проходящей через центр масс тела. В этом несложно убедиться, если получить выражение (7.6), используя не закон сохранения энергии (7.5), а решив уравнение движения для центра масс тела
Положительные направления оси В заключение найдем условие, при котором будет отсутствовать проскальзывание при качении тела. Пусть наше тело – цилиндр. Для него момент инерции
Известно, что в отсутствии скольжения сила трения не должна превышать своего максимального значения (см. также работу 1-06).
где Так что условие непроскальзывания скатывающегося цилиндра:
именно под таким углом
Экспериментальная часть Приборыи оборудование: наклонная плоскость, электрический секундомер, 1-3 цилиндра разного диаметра. Эксперимент проводят на установке, изображённой на рисунке. Начальное положение тела на наклонной плоскости в точке А фиксируется. Время движения тела на участке АВ измеряется секундомером, который подключается к розетке. При опускании тела одновременно требуется включить секундомер. Тело начинает скатываться. В конечной точке В требуется выключить секундомер. В работе определяется момент инерции тела вращения относительно оси, проходящей через его центр масс, по времени скатывания тела без скольжения по наклонной плоскости.
Порядок выполнения работы
1. Исследуемое тело установите в исходное положение и линейкой измерьте длину пути тела S по наклонной плоскости. 2. Произведите пуск тела нажатием кнопки и запишите время движения тела по автоматическому секундомеру. Установите стрелки секундомера на нуль. Повторите этот пункт 8-10 раз. 3. Взвесьте исследуемое тело. 4. Измерьте штангенциркулем диаметр 5. Проделайте действия указанные в пунктах 1-5, с другими телами. 6. Занести результаты измерения в таблицу по форме 7.1. Форма 7.1
7. Подсчитать tср для каждой серии эксперимента. 8. По формуле (7.6) вычислите экспериментальное значение момента инерции тела. Величина угла a написана на макете. 9. Вычислите по формуле (7.7) теоретический момент инерции тела и результаты запишите в таблицу. Сравните его с экспериментальным значением и укажите причину возможного несоответствия. 10. Вычислите относительную и абсолютную погрешности моментов инерции Jэкс и J теор. 11. Результаты вычисления J экс и J теор. представьте в виде
Контрольные вопросы 1. Сравните формулировки 2-го закона Ньютона – для поступательного и вращательного движения тела. 2. Что такое момент инерции твердого тела и от чего он зависит?
3. Что такое плоское движение твердого тела и что характерно для такого движения? 4. Объясните, почему кинетическую энергию тела можно представить в виде уравнения (7.4). 5. Представьте вывод формулы для момента инерции на основе закона сохранения энергии (7.6) 6. Выполните то же, что и в п. 5, используя уравнение движения (7.8), (7.9). 7. Объясните, какую роль играет сила трения покоя и получите условие скатывания цилиндра без скольжения (7.12). 8. Если учесть действие сил трения качения, к каким изменениям при определении момента инерции тела это приведет?
Используемая литература
[3] c. 53-56; [5] c. 125-128; [7] c. 17-19.
Лабораторная работа 1-08 “Исследование динамики вращательного движения на маятнике Обербека”
Цель работы: проверка основного уравнения динамики вращательного движения, определение момента инерции маятника Обербека.
Теоретическое введение
Кинематические характеристики вращательного движения. Движение твердого тела, при котором все точки прямой, жестко связанной с телом, остаются неподвижными, называется вращением тела вокруг неподвижной оси. Прямая называется осью вращения. При вращении тела вокруг закрепленной оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют следующие кинематические характеристики движения: угол поворота Характеристикой быстроты вращения служит угловая скорость тела, равная отношению вектора элементарного угла поворота тела к продолжительности этого поворота:
Вектор угловой скорости направлен по оси вращения так же, как и угловое перемещение. Быстроту изменения угловой скорости во времени характеризует угловое ускорение
При возрастании угловой скорости ω угловое ускорение Найдем связь между линейными и угловыми величинами. Величина линейного перемещения
Разделив обе части уравнения (8.3) на
Теперь продифференцируем (8.4) по времени:
где
Динамика твердого тела.
Направление момента силы определяется правилом буравчика (рис.8.1), величина момента силы
где Момент силы относительно оси характеризует способность силы вращать тело вокруг этой оси. Составляющая силы, параллельная оси, вращения тела вызвать не может, а напряжения, возникающие в оси, нас не интересуют. Тогда достаточно рассмотреть силы, направления которых перпендикулярны оси вращения ОО’ (рис.8.1). Определим плечо силы
Более того, поворот тела с закрепленной осью вращения может быть вызван только касательной составляющей силы
так как Пусть твердое тело разбито на отдельные элементарные массы Δm. Выразим касательную составляющую равнодействующей сил, приложенных к этой точке, по второму закону Ньютона:
Учитывая (8.5) для касательного ускорения, получим из (8.10) и (8.11):
Скалярная величина
равная произведению массы материальной точки на квадрат ее расстояния до оси, называется моментом инерции материальной точки относительно оси. Векторы
Уравнение (8.14) является основным законом динамики вращательного движения для материальной точки. Соотношение, аналогичное (8.12), можно записать для каждой точки тела, и затем просуммировать по всем точкам, тогда (с учетом того, что угловое ускорение одинаково для всех точек и его можно вынести за знак суммы):
В левой части равенства стоит сумма моментов всех сил (и внешних, и внутренних), приложенных к каждой точке тела. Но по третьему закону Ньютона, силы, с которыми точки тела взаимодействуют друг с другом (внутренние силы), равны по величине и противоположны по направлению и лежат на одной прямой, поэтому их моменты компенсируют друг друга. Таким образом, в левой части (8.15) остается суммарный момент только внешних сил. Сумма произведений элементарных масс на квадрат их расстояний от оси вращения называется моментом инерции твердого тела относительно данной оси:
Момент инерции
В случае непрерывного распределения массы сумма в (8.16) сводится к интегралу по всему объему тела:
Таким образом, доказан основной закон динамики твердого тела: угловое ускорение твердого тела прямо пропорционально суммарному моменту внешних сил, приложенных к телу, и обратно пропорционально моменту инерции тела относительно оси вращения
Этот закон аналогичен второму закону Ньютона при поступательном движении:
и позволяет определить угловое ускорение твердого тела. Приведем моменты инерции для некоторых однородных тел. 1. Момент инерции тонкостенного кольца (обруча) радиуса R относительно оси, проходящей через его центр и перпендикулярной его плоскости:
2. Момент инерции круглого диска (цилиндра) относительно оси, проходящей через его центр и перпендикулярной плоскости диска:
3. Момент инерции однородного полого диска (толстостенного кольца) внутренним радиусом
4. Момент инерции шара относительно оси, проходящей через его центр:
5. Момент инерции тонкого длинного стержня длиной l относительно оси, проходящей через его середину перпендикулярно стержню:
Подсчет момента инерции тела относительно произвольной оси облегчается применением теоремы Штейнера: момент инерции тела
Экспериментальная часть.
Оборудование: лабораторная установка, секундомер, штангенциркуль Описание установки.
Маятник Обербека представляет собой свободно вращающуюся на горизонтальной оси крестовину со шкивом радиуса Крестовина состоит из четырех стержней 2, закрепленных под прямым углом к оси и друг к другу. На каждый стержень надето по одинаковому грузу 3, которые можно передвигать вдоль стержня и закреплять в любой точке между его основанием и концом. Масса каждого грузика Измерения времени падения груза производятся при помощи секундомера, который включают и выключают в соответствующее время.
Методика измерения
Выведем рабочую формулу для определения момента инерции тела. Если предоставить возможность грузу
где
Сила натяжения нити
Тогда уравнение вращательного движения маятника (8.18) запишется в виде
Так как нить нерастяжима и проскальзывания нет, линейное ускорение a груза
Так как поступательное движение груза m поступательное без начальной скорости, то расстояние (высота
Решая совместно (8.24), (8.25) и (8.26), находим момент инерции маятника:
а также выражение для углового ускорения:
и момента силы:
Упражнение 1 а) Определение углового ускорения маятника Обербека и момента силы натяжения; б) проверка основного закона динамики вращательного движения:
1. Измерить штангенциркулем диаметр шкива 3 и найти его радиус 2. Закрепить грузы на концах крестовины в крайних положениях. Добиться равновесия крестовины при любом ее повороте. 3. Положить на тарелочку гирьку массой 4. Вращая крестовину рукой, намотать нить на шкив. 5. Зафиксировать тарелочку с грузом на высоте h=0.7÷0.8 от наинизшего положения. Записать величину h в таблицу по форме 8.1. 6. Освободить груз и записать в таблицу по форме 8.1 время 7. Повторить измерение времени 8. Повторить измерения (пункты 4÷6) с массой 9. Рассчитать угловые ускорения
10. Рассчитать моменты сил
11. Оценить погрешности определения 12. Все результаты занести в таблицы по форме 8.2. 13. Сравнивая
Форма 8.1.
Форма 8.2.
Замечание 1: погрешность времени
где коэффициент Стьюдента для числа опытов n=5 и доверительной вероятности α=0.95 равен: tn α=2.57; Δti=|tср.- ti|. Замечание 2: погрешности ε и М рассчитываются, исходя из формул (33) и (34) соответственно, по стандартной методике расчета погрешностей при косвенных измерениях:
где
где производные равны:
Замечание 3: абсолютные погрешности отношений (31) и (32) удобнее считать, предварительно рассчитав относительные погрешности:
Упражнение 2. а) Определение момента инерции маятника Обербека; б) проверка теоремы Штейнера. 1. Оставив грузы 2. Оставив на тарелочке массу m, повторить 5 раз измерения времени движения груза 3. Передвинуть грузы 4. Повторить измерение времени 5. Повторить измерения и вычисления по пункту 4, передвинув грузики на стержнях вплотную к шкиву, все результаты занести в таблицы по форме 8.3 и 8.4.
Форма 8.3.
Форма 8.4.
6. Оценить погрешность момента инерции 7. Рассчитать изменение момента инерции маятника Обербека при передвижении грузов с конца стержней на середину по формулам:
где m 0 = 0.12 кг. 8. Сравнить изменение момента инерции маятника Обербека, рассчитанного с использованием теоремы Штейнера по формулам (8.35) и (8.36) и полученного экспериментально по данным табл. 8.3:
9. Сделать выводы. Замечание 1: погрешность времени Замечание 2: погрешность
где производные равны:
Контрольные вопросы
1. Дайте определение углового перемещения, угловой скорости и ускорения. Как направлены эти вектора? 2. Запишите формулы, связывающие линейные и угловые величины перемещения, скорости, ускорения. 3. Что такое момент силы относительно точки? Относительно оси? От чего он зависит? Как направлен вектор момента силы? 4. Что такое момент инерции материальной точки, твердого тела, от чего он зависит? 5. Сформулируйте и докажите основной закон динамики вращательного движения (8.18). 6. Сформулируйте теорему Штейнера и
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.145.155 (0.016 с.) |

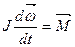 (7.1)
(7.1) – момент инерции тела,
– момент инерции тела, 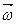 – угловая скорость,
– угловая скорость,  – угловое ускорение,
– угловое ускорение,  – полный момент внешних сил.
– полный момент внешних сил.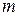 , а момент инерции
, а момент инерции 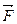 , а момент силы относительно оси
, а момент силы относительно оси  (
( - номер частиц), которые можно рассматривать как материальные точки с неизменными расстояниями между ними. При этом
- номер частиц), которые можно рассматривать как материальные точки с неизменными расстояниями между ними. При этом 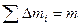 - масса всего тела. В результате задача сводится к задаче о вращении системы материальных точек вокруг оси. Из решения ее следует, что момент инерции тела
- масса всего тела. В результате задача сводится к задаче о вращении системы материальных точек вокруг оси. Из решения ее следует, что момент инерции тела 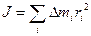 (7.2)
(7.2) . Вектор
. Вектор 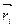 лежит в плоскости вращения массы
лежит в плоскости вращения массы  еще ничего не говорит о величине его момента инерции
еще ничего не говорит о величине его момента инерции 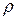 сумма в (7.2) заменится на интеграл по всему объему тела. Каждый из элементарных объемов тела
сумма в (7.2) заменится на интеграл по всему объему тела. Каждый из элементарных объемов тела 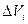 массой
массой 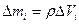 при переходе к бесконечно малым заменяем на
при переходе к бесконечно малым заменяем на  и соответственно
и соответственно (7.3)
(7.3) меняется от точки к точке
меняется от точки к точке  . Если эта зависимость известна, тогда нужно вычислить тройной интеграл
. Если эта зависимость известна, тогда нужно вычислить тройной интеграл 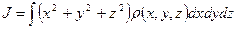 . Это несложно делать для однородных (
. Это несложно делать для однородных (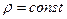 ) симметричных твердых тел, вращающихся вокруг неподвижной оси, проходящей через центр масс (центр тяжести). Далее будут еще приведены выражения для моментов инерции шара, цилиндра, пустотелого цилиндра.
) симметричных твердых тел, вращающихся вокруг неподвижной оси, проходящей через центр масс (центр тяжести). Далее будут еще приведены выражения для моментов инерции шара, цилиндра, пустотелого цилиндра. и массой
и массой  к горизонту с высоты
к горизонту с высоты  (рис. 7.1), с использованием закона сохранения энергии.
(рис. 7.1), с использованием закона сохранения энергии.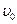
 (7.4)
(7.4)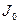 – момент инерции тела относительно оси вращения, проходящей через его центр масс,
– момент инерции тела относительно оси вращения, проходящей через его центр масс,  – угловая скорость тела,
– угловая скорость тела,  (7.5)
(7.5)
 и составляющей силы тяжести. Поэтому, если обозначим через
и составляющей силы тяжести. Поэтому, если обозначим через  длину наклонной плоскости (
длину наклонной плоскости (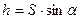 ) и считаем, что тело движется с нулевой начальной скоростью, то можно записать
) и считаем, что тело движется с нулевой начальной скоростью, то можно записать ;
; 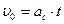 ;
;  ;
;  ,
, – время движения тела по наклонной плоскости.
– время движения тела по наклонной плоскости. .
.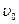 и
и  , то получим
, то получим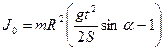 (7.6)
(7.6) ;
; ; (7.7)
; (7.7)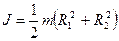 , где
, где 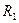 и
и  - внешний и внутренний радиусы цилиндра;
- внешний и внутренний радиусы цилиндра;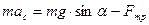 (7.8)
(7.8) (7.9)
(7.9)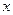 и
и  указаны на рис 7.1.
указаны на рис 7.1.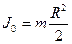 . Если проскальзывания нет, то ускорение поступательного движения цилиндра при скатывании известным образом связано с угловым ускорением
. Если проскальзывания нет, то ускорение поступательного движения цилиндра при скатывании известным образом связано с угловым ускорением  :
: 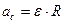 . Подставив эти определения в уравнения (7.8) и (7.9), получим из этих уравнений выражение для сил трения
. Подставив эти определения в уравнения (7.8) и (7.9), получим из этих уравнений выражение для сил трения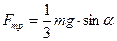 (7.10)
(7.10)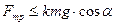 (7.11)
(7.11)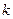 -коэффициент трения покоя.
-коэффициент трения покоя. (7.12)
(7.12)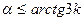 следует устанавливать наклонную плоскость при скатывании цилиндра для определения момента инерции.
следует устанавливать наклонную плоскость при скатывании цилиндра для определения момента инерции. тела 10 раз.
тела 10 раз.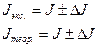
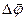 , угловую скорость
, угловую скорость  и угловое ускорение
и угловое ускорение 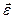 . Роль перемещения
. Роль перемещения  при вращательном движении играет вектор малого поворота (угловое перемещение)
при вращательном движении играет вектор малого поворота (угловое перемещение)  . (8.1)
. (8.1)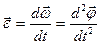 . (8.2)
. (8.2)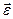 совпадает с ней по направлению, при убывании – направлено в противоположную сторону.
совпадает с ней по направлению, при убывании – направлено в противоположную сторону.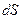 точки, вращающейся по окружности радиуса
точки, вращающейся по окружности радиуса 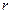 :
: . (8.3)
. (8.3)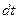 , получим:
, получим:  . Так как производная пути по времени – это величина скорости:
. Так как производная пути по времени – это величина скорости:  , а
, а 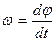 (8.1), то:
(8.1), то: . (8.4)
. (8.4)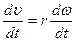 , или:
, или: , (8.5)
, (8.5) – касательное (тангенциальное) ускорение, определяющее быстроту изменения модуля скорости
– касательное (тангенциальное) ускорение, определяющее быстроту изменения модуля скорости  :
: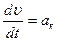 . (8.6)
. (8.6)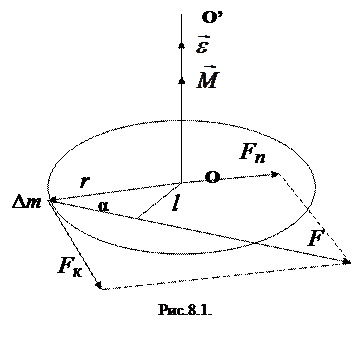 Пусть на тело действует сила
Пусть на тело действует сила  . Моментом силы
. Моментом силы  , проведенного из точки О в точку приложения силы, на вектор силы
, проведенного из точки О в точку приложения силы, на вектор силы  . (8.7)
. (8.7) , (8.8)
, (8.8) относительно оси ОО’ как расстояние от оси вращения до линии действия силы, тогда
относительно оси ОО’ как расстояние от оси вращения до линии действия силы, тогда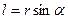 ,
, . (8.9)
. (8.9) , причем эта составляющая тем успешнее осуществит поворот, чем больше ее плечо r:
, причем эта составляющая тем успешнее осуществит поворот, чем больше ее плечо r: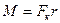 , (8.10)
, (8.10)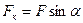 .
. . (8.11)
. (8.11) . (8.12)
. (8.12) , (8.13)
, (8.13) и
и 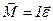 . (8.14)
. (8.14) . (8.15)
. (8.15) . (8.16)
. (8.16) твердого тела является мерой инертных свойств твердого тела при вращательном движении и аналогичен массе тела во втором законе Ньютона. Он существенно зависит не только от массы тела, но и от ее распределения относительно оси вращения (в направлении, перпендикулярном оси).
твердого тела является мерой инертных свойств твердого тела при вращательном движении и аналогичен массе тела во втором законе Ньютона. Он существенно зависит не только от массы тела, но и от ее распределения относительно оси вращения (в направлении, перпендикулярном оси).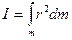 . (8.17)
. (8.17) . (8.18)
. (8.18)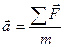 (8.19)
(8.19)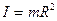 . (8.20)
. (8.20) . (8.21)
. (8.21) и внешним радиусом
и внешним радиусом  относительно оси, проходящей через центр масс перпендикулярно плоскости диска:
относительно оси, проходящей через центр масс перпендикулярно плоскости диска: . (8.22)
. (8.22)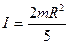 . (8.23)
. (8.23) . (8.24)
. (8.24)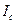 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния
относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния 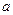 между осями
между осями . (8.20)
. (8.20)
 г. На шкив 4 навита привязанная к нему одним концом нить 5, на другом конце которой подвешивается гиря 7 массы
г. На шкив 4 навита привязанная к нему одним концом нить 5, на другом конце которой подвешивается гиря 7 массы 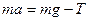 , (8.21)
, (8.21)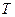 – сила натяжения нити. Отсюда
– сила натяжения нити. Отсюда . (8.22)
. (8.22) . (8.23)
. (8.23)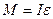 , или:
, или: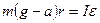 . (8.24)
. (8.24)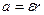 . (8.25)
. (8.25) , откуда находим ускорение:
, откуда находим ускорение: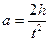 . (8.26)
. (8.26)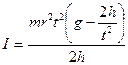 , (8.27)
, (8.27) (8.28)
(8.28)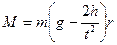 . (8.29)
. (8.29)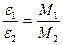 (при
(при  ). (8.30)
). (8.30) (около 100 г).
(около 100 г). его опускания.
его опускания. (150÷200 г), заменив гирьки на тарелочке.
(150÷200 г), заменив гирьки на тарелочке.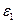 и
и  по формуле (8.28), найти их отношение
по формуле (8.28), найти их отношение . (8.31)
. (8.31) и
и  по формуле (8.29), найти их отношение
по формуле (8.29), найти их отношение . (8.32)
. (8.32) и их отношений
и их отношений  , и сделать вывод.
, и сделать вывод.
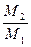
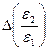
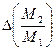
 рассчитывается по стандартной методике расчета погрешностей случайной величины:
рассчитывается по стандартной методике расчета погрешностей случайной величины: , (8.38)
, (8.38) ,
, ,
,  ,
, 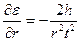 .
. ,
,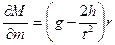 ,
, 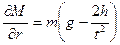 ,
,  ,
,  .
. ;
;  . (8.34)
. (8.34)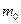 на концах стержней, измерить расстояние R 1 от центра тяжести грузов на стержнях до оси вращения.
на концах стержней, измерить расстояние R 1 от центра тяжести грузов на стержнях до оси вращения. движения груза m 5 раз, рассчитать среднее время и момент инерции
движения груза m 5 раз, рассчитать среднее время и момент инерции  крестовины для нового положения грузиков на стержнях.
крестовины для нового положения грузиков на стержнях.

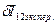
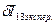
 .
.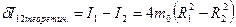 , (8.35)
, (8.35) , (8.36)
, (8.36)

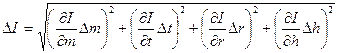 ,
, ;
; 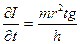 ;
; 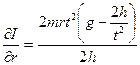 ;
;  .
.


