
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы теории вероятностей и математической статистки»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теория вероятностей - математическая наука, изучающая закономерности случайных явлений. Знание закономерностей, которым подчиняются массовые случайные события, позволяют предвидеть, как эти события будут протекать. Методы теории вероятностей широко применяются в различных отраслях науки и техники: в теории надежности, в теории массового обслуживания, теоретической физике, астрономии, теории ошибок, теории управления, теории связи и во многих других теоретических и прикладных науках. Теория вероятности служит для обоснования математической статистики. Математическая статистка - раздел математики, изучающий методы сбора, систематизации и обработки результатов наблюдений с целью выявления статистических закономерностей. Методы математической статистики применяются при планировании организации производства, анализе технологических процессов, для контроля качества продукции и многих других целей. Статистические программные пакеты сделали методы теории вероятностей и математической статистики более доступными и наглядными, так как трудоемкую работу по расчету статистик, параметров, характеристик, построение таблиц и графиков в основном стал выполнять компьютер, а исследователю осталось выполнить постановку задачи, выбор метода решения и интерпретацию результатов. Основными методами, используемые в теории вероятностей, являются следующие: 1.классическая метод: Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу: P(A) = m/n, где m-число элементарных исходов, благоприятствующих А; n-число всех возможных элементарных исходов испытания. 2.геометрическая метод: вероятность попадания точки в область(отрезок, часть плоскости и т.д.). Пусть отрезок l составляет часть отрезка L. На отрезок L на удачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством. P= Длинаl/длинаL. 3.теорема сложения вероятностей: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: Р(А)+Р(В)=Р(А)+Р(В)-Р(А*В) 4.теорема произведения событий: Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий другими словами логическое И. Вероятность появления двух зависимых событий равна произведению вероятностей одного из них на вероятность другого вычисленную при условии, что первое событие имело место: Р(А*В)=Р(А)*Р(В/А)=Р(В)*Р(В/А). Вероятность произведения нескольких событий равна произведению вероятностей этих событий причем вероятность каждого следующего события вычисляется при условии, что все предыдущие имели место. Р(А1;А2…Аn)=Р(А1)*Р(А2/А1)*… *Р(Аn/А1,А2…Аn-1). 5.формула полной вероятности: пусть событие А может появиться вместе с одним из образующих полную группу попарнонесовместных событий Н1,Н2…Нn называемых гипотезами, тогда вероятность события А вычисляется как сумма произведений вероятностей каждой гипотезы на вероятность события А при этой гипотезе 6.формула Бернулли: испытания проводимые по данной формуле должны быть независимы, количество их должно быть известно заранее и в результате должны произойти два исхода: успех или неуспех. Вероятность того, что в n испытаниях успех осуществится ровно k раз следовательно, неуспех (n-k) раз, вычисляется по следующей формуле: 7. формула Байеса: пусть имеется полная группа попарнонесовместных гипотез Н1,Н2…Нn с известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло: Основными методами математической статистики являются следующие: 1. однофакторный и многофакторный корреляционный анализ - применяется для установления факта зависимости или независимости исследуемой случайной величины от одного или нескольких факторов – рассчитываются коэффициенты коэффициента множественной корреляции R. Степень влияния значения конкретного фактора x на результативный показатель Y оценивается с помощью коэффициента парной корреляции rY,x,
На основании полученных коэффициентов множественной корреляции строится матрица парных коэффициентов, после чего делается вывод о взаимосвязи факторов с результирующим показателем. 2.регресионный анализ – получение регрессионной модели, т.е. функциональной зависимости результативного показателя Y от значений выбранных факторов. Количественными характеристиками качественности выбранной модели на основании регрессионного анализа чаще всего используются коэффициент множественной корреляции R и коэффициент детерминации R2. Коэффициент множественной корреляции (индекс корреляции) R считается универсальным, т.к. отражает тесноту связи и точность модели. Чем ближе значение коэффициента к 1, тем точнее построенная модель. Коэффициент детерминации R2 показывает долю вариации значений показателя Y под воздействием изучаемых факторов. То есть коэффициент позволяет количественно определить, какая доля изменений показателя Y учтена в модели и обусловлена влиянием на него факторов. 3.коэффииценный анализ - оценка влияния отдельных факторов регрессионной модели на величину результативного показателя Y. Рассчитываются такие коэффициенты: 1. Коэффициент эластичности показывает, на сколько процентов изменится зависимая величина показателя Y при изменении фактора xj на 1%. Однако он не учитывает степень колеблемости факторов. 2.Бета-коэффициент позволяет определить, на какую часть величины среднего квадратического отклонения где 3 .дельта-коэффициент - позволяет оценить долю влияния каждого фактора xj в суммарном влиянии всех факторов:
Метод Монте-Карло. Моделирование по методу Монте-Карло представляет собой автоматизированную математическую методику, предн. для учета риска в процессе количеств. анализа и принятия решений. Эта методика применяется профессионалами в разных областях, таких как финансы, управление проектами, энергетика, производство, проектирование, НИОКР, страхование, нефтегазовая отрасль, транспорт и охрана окружающей среды. Моделирование по методу Монте-Карло позволяет специалисту, принимающему решения, рассматривать целый спектр возможных последствий и оценивать вероятность их наступления. Этот метод демонстрирует возможности, лежащие на противоположных концах спектра, а также последствия решений.В рамках метода М-К анализ риска выполн.с помощью моделей возможных результатов. При создании таких моделей любой фактор, которому свойственна неопределенность, заменяется диапазоном значений — распределением вероятностей. Затем выполняются многократные расчеты результатов, причем каждый раз используется другой набор случайных значений функций вероятности. Порой для завершения моделирования бывает необходимо произвести тысячи и даже десятки тысяч перерасчетов. Моделирование по методу Монте-Карло позволяет получить распределения значений возможных последствий.Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а: М(Х)=а.Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое - Логнормальное распределение. Такое распределение используется для отражения величин, которые не опускаются ниже нуля, но могут принимать неограниченные положительные значения. (например, стоимость недвижимого имущества, цены на акции) - Равномерное распределение. Все величины могут с равной вероятностью принимать то или иное значение, пользователь просто определяет минимум и максимум(производственные издержки) - Треугольное распределение, Дискретное распределение. Пользователь определяет конкретные значения из числа возможных, а также вероятность получения каждого из них. Моделирование по методу Монте-Карло дает гораздо более полное представление о возможных событиях. Оно позволяет судить не только о том, что может произойти, но и о том, какова вероятность такого исхода. Моделирование по методу Монте-Карло имеет ряд преимуществ: Вероятностные результаты. Результаты демонстрируют не только возможные события, но и вероятность их наступления.- Графическое представление результатов. Характер данных, позволяет создавать графики различных последствий, а также вероятностей их наступления. Это важно при передаче результатов другим заинтересованным лицам.- Анализ чувствительности. При проведении моделирования по методу Монте-Карло несложно увидеть, какие исходные данные оказывают наибольшее воздействие на конечные результаты.- Анализ сценариев. Применяя метод Монте-Карло, аналитики могут точно определить, какие исходные данные приводят к тем или иным значениям, и проследить наступление определенных последствий. Это очень важно для проведения дальнейшего анализа.- Корреляция исходных данных. Метод Монте-Карло позволяет моделировать взаимозависимые отношения между исходными переменными. Для получения достоверных сведений необходимо представлять себе, в каких случаях при увеличении некоторых факторов соответствующим образом возрастают или снижаются другие.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 5864; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.50 (0.008 с.) |


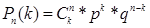 , где Сnk-число сочетаний из n-элементов k, p - вероятность успеха, q - вероятность неуспеха, где q = 1-р.
, где Сnk-число сочетаний из n-элементов k, p - вероятность успеха, q - вероятность неуспеха, где q = 1-р.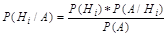 .
.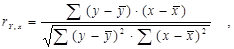
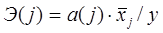
 изменится зависимая величина Y с изменением соответствующей независимой переменной xj на величину своего среднего квадратического отклонения
изменится зависимая величина Y с изменением соответствующей независимой переменной xj на величину своего среднего квадратического отклонения  при фиксированном значении остальных независимых переменных.
при фиксированном значении остальных независимых переменных.  ,
,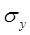 - среднее квадратическое отклонение зависимой величины Y,
- среднее квадратическое отклонение зависимой величины Y,  - среднее квадратическое отклонение фактора xj:
- среднее квадратическое отклонение фактора xj: 

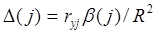 , где ryj - коэффициент парной корреляции между фактором xj (j=1,…,m) и зависимой величиной Y; R2- коэффициент детерминации.
, где ryj - коэффициент парной корреляции между фактором xj (j=1,…,m) и зависимой величиной Y; R2- коэффициент детерминации.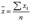 и принимают x в качестве оценки (приближённого значения) a* искомого числа a:
и принимают x в качестве оценки (приближённого значения) a* искомого числа a: 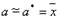 Этот часто наз. методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину Х, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*.При использовании распределений вероятностей переменные могут иметь разные вероятности наступления разных последствий. Нормальное распределение (или «гауссова кривая»). Чтобы описать отклонение от среднего, пользователь определяет среднее или ожидаемое значение и стандартное отклонение. Значения, расположенные посредине, рядом со средним, характеризуются наиболее высокой вероятностью. Нормальное распределение симметрично и описывает множество обычных явлений.(например темпы инфляции и цены на энергоносители)
Этот часто наз. методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину Х, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*.При использовании распределений вероятностей переменные могут иметь разные вероятности наступления разных последствий. Нормальное распределение (или «гауссова кривая»). Чтобы описать отклонение от среднего, пользователь определяет среднее или ожидаемое значение и стандартное отклонение. Значения, расположенные посредине, рядом со средним, характеризуются наиболее высокой вероятностью. Нормальное распределение симметрично и описывает множество обычных явлений.(например темпы инфляции и цены на энергоносители)


