
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарная теория вероятностей и случайных процессовСодержание книги
Поиск на нашем сайте Тема 0. Основные этапы становления теории вероятностей и математической статистики. – 4 часа лекций
В истории развития теории вероятностей выделяют следующие этапы. 1. Предыстория теории вероятностей. Начало этого периода «теряется в дали веков», ставились и решались примитивные задачи, которые позже будут отнесены к теории вероятностей. Никаких специальных методов в этот период не возникает, идет накопление материала. Этот период заканчивается в 16 веке работами Кардано, Пачоли, Н. Тарталья и др. 2. Возникновение теории вероятностей как науки. В этот период вырабатываются первые специфические понятия, такие, как математическое ожидание. Устанавливаются первые теоремы – теоремы сложения и умножения вероятностей. Начало этого периода связано с именами Б. Паскаля, П. Ферма, Х. Гюйгенса. Этот период продолжается от середины 17 века до начала 18 века. В это время теория вероятностей находит свои первые применения в демографии, страховом деле, в оценке ошибок наблюдения. 3. Следующий период начинается с появления работы Я. Бернулли «Искусство предположения» (1713). Это первая работа, в которой была строго доказана предельная теорема – простейший случай закона больших чисел. Теорема Бернулли дала возможность широко применять теорию вероятностей к статистике. К этому периоду относятся работы А. Муавра, П.-С. Лапласа, Ф. Гаусса, С.-Д. Пуассона и др. Теория вероятностей начинает применяться в различных областях естествознания. Центральной проблемой этого периода является доказательство предельных теорем. 4. Следующий период развития теории вероятностей связан, прежде всего, с русской (Петербургской) школой. Здесь следует назвать имена П.Л. Чебышева, А.А. Маркова, А.М. Ляпунова. В этот период распространение закона больших чисел и центральной предельной теоремы достигает своих естественных границ. Законы теории вероятностей стали применяться к зависимым случайным величинам. Все это дало возможность приложения теории вероятностей ко многим разделам естествознания, в первую очередь – физике. Возникает статистическая физика, которая развивается во взаимосвязи с теорией вероятности. 5. Современный период теории вероятностей начался с установления аксиоматики. Этого в первую очередь требовала практика, так как для успешного применения теории вероятностей к физике, биологии и другим естественным наукам, а также технике и военному делу необходимо было уточнить и привести в стройную систему ее основные части и понятия. Благодаря аксиоматике теория вероятностей стала абстрактно-дедуктивной математической дисциплиной, тесно связанной с теорией множеств, а через нее – с другими математическими дисциплинами. Это обусловило необычайную широту использования теории вероятностей, начиная от хозяйственно-прикладных вопросов и кончая самыми «тонкими» проблемами кибернетики. Первые работы этого периода связаны с работами Э. Бореля, С.Н. Бернштейна, Мизеса. Окончательное установление аксиоматики произошло в 30-е годы 20 века, когда была опубликована и получила всеобщее признание аксиоматика А.Н. Колмогорова. В последние годы намечаются новые подходы к основным понятиям теории вероятностей, в том числе и с позиций теории информации, теории игр.
Случайные события Тема 1. Предмет теории вероятностей. Случайные события, их классификация. События независимые, совместные и несовместные. Действия над событиями. Алгебра событий (теоретико-множественная трактовка). Диаграммы Эйлера-Венна. – 4 часа: 2 часа лекции, 2 часа семинарское занятие
Имеется множество задач, для решения которых приходится учитывать не только основные факторы, закономерности, которые позволяют предвидеть результат опыта (наблюдения, эксперимента) по его начальным условиям (они называются детерминистическими, определенными), но и случайные факторы, придающие исходу опыта элемент случайности, неопределенности. Выявленные в таких опытах (задачах) закономерности, называются статистическими (или вероятностными). Теория вероятностей – математическая наука, изучающая закономерности, присущие массовым случайным явлениям. В теории вероятностей рассматриваются не сами явления природы, реальные явления, а их упрощенные схемы – математические модели. Предметом теории вероятностей являются математические модели случайных явлений. Под случайным явлением понимают явление, предсказать исход которого невозможно: при неоднократном воспроизведении оно протекает всякий раз по-разному, несколько иначе, по-иному. Цель теории вероятностей – осуществление прогноза в области случайных явлений, влияние на ход этих явлений, контроль их, ограничение сферы деятельности случайности. Пусть проводится некоторый опыт (эксперимент, наблюдение, испытание), исход которого предсказать заранее нельзя. Такие эксперименты в теории вероятностей называются случайными. Все события (явления, результаты опыта или наблюдения) можно разделить на: - достоверные, - невозможные, - случайные. Случайным событием (или просто: событием) будем называть любой исход опыта, который может произойти или не произойти. Случайные события обозначаются, как правило, заглавными буквами латинского алфавита: А, В, С, … Пример. Испытание – бросается монета (вытаскивается карта, бросается кубик). Возможные события – выпадение «герба» или «решки» (появление, например, Дамы, выпадение четного числа очков на грани кубика). В теоретико-множественной трактовке случайным событием А или просто – событием А называется любое подмножество множества Ω, если само Ω конечно или счетно (т.е. элементы этого множества можно перенумеровать с помощью множества натуральных чисел). Принято обозначение А Например, случайными являются следующие события: - при телефонном звонке абонент оказался занят; - при бросании игральной кости выпало 2 очка и пр. Элементарные события, входящие в подмножество А пространства Ω, называются благоприятствующими событию А. Событие называется достоверным, если оно обязательно наступит в результате данного опыта. По определению достоверным событием является Ω. Событие называется невозможным, если оно заведомо не произойдет в результате проведения опыта. Оно обозначается через Ø. Несколько событий в данном опыте называются равновозможными, если ни одно из них не является объективно более возможным, чем другие, т.е. все события имеют «равные шансы». Действия над событиями Суммой событийА и В называется событие С, С = А + В, состоящее в наступлении хотя бы одного из них: т.е. или А, или В, или в их одновременном появлении – «А и В вместе». В теоретико-множественной трактовке суммой событийА Суммой нескольких событий называется такое событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из суммируемых событий. Произведением событий А и В называется событие С, С = А·В, состоящее в совместном наступлении этих событий, т.е. и А и В одновременно. Обозначается такое результирующее событие А·В. В теоретико-множественной трактовке произведение событийА Разностью событий А и В называется событие С = А - В, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В. Обозначается А - В. В теоретико-множественной трактовке разность событий А Противоположным событию А называется событие Ᾱ (читается «не А»), которое происходит тогда и только тогда, когда не происходит события А, т.е. Ᾱ означает, что событие А не наступило. В теоретико-множественной трактовке противоположным событию А Событие Авлечет за собой событие В (или А является частным случаем события В), если из того, что происходит событие А, следует, что происходит событие В. Записывается А Теоретико-множественная трактовка: событие Авлечет событие В (обозначается А По определению: Ø Если А Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте, т.е. они не смогут произойти вместе в одном опыте. В противном случае они называются совместными. В теоретико-множественной трактовке события А и В называются несовместными, если их произведение есть невозможное событие, т.е. их произведение А·В = Ø. События А 1, А 2, А 3, А n называются попарно-несовместными, если любые два из них несовместны. Несколько событий образуют полную группу, если они попарно несовместны, и в результате каждого опыта происходит одно и только одно из них. События А и В называются независимыми, если вероятность появления одного из них не зависит от того, произошло или не произошло другое событие. Свойства операций над событиями также наглядно представляются диаграммами Эйлера – Венна.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.64.124 (0.01 с.) |

 Ω.
Ω. и В
и В  В) – это множество, содержащее элементы, принадлежащие хотя бы одному из событий А и В.
В) – это множество, содержащее элементы, принадлежащие хотя бы одному из событий А и В.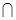 В) – множество, состоящее из элементов, общих для событий А и В.
В) – множество, состоящее из элементов, общих для событий А и В.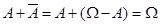 .
.


