
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи, рассмотренные на Лекции и Семинаре 2.1.Содержание книги
Поиск на нашем сайте
Задача 1-Т2.1. Одновременно бросаются два игральных кубика (игральные кости). Найти вероятность того, что сумма очков: а) равна 1; б) меньше 13; в) меньше 5; г) меньше 10.
Задача 2-Т2.1 (для самостоятельного решения). Если подбросить одновременно три игральные кости, то сколько имеется вариантов – комбинаций выброшенных очков?
Задача 3–Т2.1. В чемпионате по футболу, который проводится по системе «одного круга», участвовало 7 команд. Каждая команда сыграла по одной игре с каждой командой. Сколько всего было игр?
Задача 4-Т2.1. Пусть из пункта А в пункт В имеется 5 дорог, а из пункта В в пункт С – 6 дорог. 1) Сколько существует различных вариантов проезда из А в С? 2) Сколько существует различных вариантов проезда из пункта А в пункт В и обратно? 3) Сколько существует различных вариантов проезда из пункта А в пункт В и обратно при условии, что дороги туда и обратно будут разными?
Задача 5-Т2.1. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если а) цифры не повторяются? б) цифры могут повторяться?
Задача 6-Т2.1. Сколько различных трехзначных чисел можно составить из цифр 0, 2, 3, 5 и 7, если а) цифры не повторяются? б) цифры могут повторяться?
Задача 7-Т2.1 (самостоятельно). В одной из стран автомобильные номера из четырех цифр (нуль может стоять и на первом месте) записываются на пластинках пяти различных цветов, поскольку каждый из пяти штатов этой страны имеет номера своего цвета. Сколько разных пластин с номерами может быть выдано автовладельцам в этой стране?
Задача 8-Т2.1 (самостоятельно). Десять участников конференции обменялись визитными карточками (каждый вручил свою карточку другим участникам). Сколько всего карточек было роздано?
Задача 9-Т2.1 (самостоятельно). Десять участников конференции обменялись рукопожатиями, пожав руку каждому. Сколько всего рукопожатий было сделано?
Задача 10-Т2.1. На 10 карточках написаны буквы: А, А, А, А, А, Р, Р, Р, Д, Д. Наугад берется 5 карточек и прикладывается одна к другой слева направо. Какова вероятность того, что случайно будет сложено слово «РАДАР»?
Задача 11-Т2.1. В студенческой группе 14 девушек и 6 юношей. Сколькими способами для выполнения различных упражнений в парах можно выбрать студентов одного пола?
Задача 12-Т2.1. В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика наудачу вынимают один шар. Определить, какова вероятность, что извлеченный шар окажется цветным.
Задача 13-Т2.1. Сколькими способами могут быть распределены три призовых места среди 16 участвующих в соревновании студентов?
Задача 14–Т2.1. Из колоды в 36 карт наугад последовательно без возвращения вытянуто две карты. Найти вероятность того, что обе они – тузы.
Задача 15-Т2.1. Игральную кость бросают четыре раза. Что более вероятно: то, что шестерка появится хотя бы один раз, или же, что шестерка не появится ни разу?
Домашнее задание 2.1 – Тема 2.1 Элементы комбинаторики: Правило Суммы, Правило Произведения
Задача 1Д-Т2.1. В русском языке 33 буквы 10 гласных, 21 согласная и две специальные буквы (Ь и Ъ). Два студента независимо друг от друга выбрали по одной букве русского алфавита. Какова вероятность того, что: а) были выбраны различные буквы; б) обе выбранные буквы – гласные; в) среди выбранных букв имеются согласные? г) это две соседние буквы алфавита.
Задача 2Д-Т2.1. Из пяти чисел 1, 2, 3, 4, 5 поочередно выбираются два. Найдите вероятность того, что: а) первое из чисел меньше второго; б) эти два числа – дины катетов прямоугольного треугольника с целочисленной гипотенузой; в) произведение этих чисел оканчивается нулем; г) первое из чисел делится на второе.
Задача 3Д-Т2.1. Случайно и поочередно нажимают три клавиши одной октавы. Найдите вероятность того, что: а) не была нажата «фа»; б) не были нажаты ни «до», ни «си»; в) была нажата «ля»; г) получилось до-мажорное трезвучие «до-ми-соль».
Задача 4Д-Т2.1. Двое независимо друг от друга записали по одному двузначному натуральному числу. Найдите вероятность того, что: а) эти два числа различны; б) сумма чисел равна 100; в) сумма чисел не больше 25; г) сумма чисел больше 190.
Задача 5Д-Т2.1. Набирая номер телефона, абонент забыл две последние цифры и набрал их наугад. Найти вероятность того, что были набраны нужные цифры.
Задача 6Д–Т2.1. Из колоды в 36 карт наугад вытянуто последовательно без возвращения две карты. Найти вероятность того, что обе они – тузы.
Задача 7Д-Т2.1. В студенческой группе 12 девушек и 16 юношей. Сколькими способами можно выбрать для вручения разных призов студентов одного пола?
Задача 8Д-Т2.1. Если подбросить одновременно три игральные кости, то сколько имеется различных комбинаций выброшенных очков?
Задача 9Д-Т2.1. В цветочном киоске 7 видов цветов. Сколькими способами можно составить букет из трех цветов?
Задача 10Д-Т2.1. Из пункта А в пункт В можно добраться самолетом, поездом, автобусом. Из пункта В в пункт С – пешком, на тракторе, на лошади, на лодке. Сколькими способами можно выбрать дорогу от пункта А до пункта С через В?
Задача 11Д-Т2.1. Сколькими способами можно выбрать один цветок из корзины, в которой находятся 12 гвоздик, 15 роз и 7 хризантем?
Задача 12Д-Т2.1. Сколько имеется пятизначных чисел, все цифры у которых различны?
Задача 13Д-Т2.1. Сколькими способами можно составить трехцветный полосатый флаг (три горизонтальные полосы), если имеется материя пяти различных цветов?
Задача 14Д-Т2.1. Из группы в 15 человек выбирают 4-х участников эстафеты 800х400х200х100. Сколькими способами можно расставить спортсменов на этапах?
Задача 15Д-Т2.1. Какова вероятность того, что произвольно взятое трехзначное число делится на 3?
Задача 16Д-Т2.1. Некто написал на листочке четырехзначное число. Какова вероятность отгадать его с первой попытки?
Задача 17Д-Т2.1. В урне находятся 10 белых, 15 черных и 20 красных шаров. Сколькими различными способами можно вытащить из урны 3 шара разных цветов?
Задача 18Д-Т2.1. Группа студентов изучает 10 различных дисциплин. Сколькими способами можно составить расписание занятий в понедельник, если в этот день должно быть 4 разных занятия?
Задача 19Д-Т2.1. Из 10 мальчиков и 10 девочек спортивного класса для участия в эстафете надо составить три команды, каждая из которых состоит из мальчика и девочки. Сколькими способами это можно сделать?
Задача 20Д-Т2.1. Сколько можно составить четырехзначных чисел так, чтобы любые две соседние цифры были различны? Тема 3. Элементы комбинаторики. Понятие о «схеме выбора». Схема выбора без возвращения: Перестановки, Размещения, Сочетания. – 4 часа: 2 часа лекции, 2 часа семинарское занятие
Существуют две схемы выбора m элементов из множества, состоящего из n элементов: - без возвращения, когда выбранные элементы после извлечения не возвращаются в исходное множество; - с возвращением, когда выбор осуществляется поэлементно с обязательным возвращением отобранного элемента в исходное множество на каждом шаге выбора. Схема выбора без возвращений. Соединения. Виды соединений Пусть А – совокупность некоторых n объектов (предметов, элементов и пр.) а 1, а 2, … а n, объединенных некоторым признаком или свойством. Из различных элементов множества А можно образовать группы. Если в каждую группу входит одно и то же количество элементов, например, m (m ≤ n), взятых из множества А, то говорят, что они образуют соединения из n элементов по m в каждом. В зависимости от того, входят ли в соединение все элементы множества А,- или только часть элементов этого множества, имеет ли значение порядок следования элементов, или порядок следования элементов значения не имеет, под общим именем соединений принято понимать следующие три типа комбинаций: перестановки; размещения; сочетания. Перестановки Перестановками называются такие изменения, в результате которых количество выбираемых предметов сохраняется, а порядок их извлечения может изменяться случайным способом. Определение 1. Соединения, в которые входят все n элементов множества А и которые отличаются только порядком следования элементов, называются перестановками из n элементов. Количество перестановок обозначается Число перестановок Р из n элементов равно:
Произведение n· (n - 1) · (n - 2) ·… · 1 называется факториалом числа n, обозначается символом n!, который читается «эн-факториал». Принято, что 0! = 1 и 1! = 1. Размещения Определение 2. Соединения, каждое из которых содержит m различных элементов (m ≤ n), взятых из n элементов множества А, отличающихся друг от друга или составом элементов или порядком расположения элементов, называются размещениями из n элементов по m в каждом. Число таких размещений обозначается символом Число возможных размещений из n элементов по m в каждом равно произведению m последовательно убывающих на единицу чисел, из которых большее есть n, т.е.
Это еще одна, на мой взгляд, более удобная расчетная формула для Размещений. По определению, перестановки являются частным случаем размещений, когда m = n: Рn = А Сочетания Сколькими способами можно выбрать из n различных объектов (предметов) m штук? Определение 3. Соединения, каждое из которых содержит m различных элементов (m ≤ n), взятых из n элементов множества А, отличающихся друг от друга по крайней мере одним элементом, называются сочетаниями из n элементов по m. Число таких сочетаний обозначается символом Из определения следует, что сочетания отличаются друг от друга хотя бы одним элементом, т.е. составом входящих элементов. Изменение порядка следования элементов внутри одного сочетания не приводит к образованию нового сочетания. Число всех возможных сочетаний из n элементов по m в каждом выражается формулой
Факториальная запись этой формулы.
Свойства Сочетаний (биномиальных коэффициентов) Сочетания - 1. «Правило симметрии»: для всех m = 0, 1, …, n (записывается:
«Правило симметрии» удобно использовать в расчетах количества сочетаний 2. Сумма всех биномиальных коэффициентов равна 2n, т.е.
3. Правило Паскаля:
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.206.229 (0.007 с.) |

 и читается «Пэ из эн».
и читается «Пэ из эн».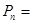

 , читается «А из эн по эм».
, читается «А из эн по эм».

 .
. или
или  и читается «цэ из эн по эм».
и читается «цэ из эн по эм».

 , т.е. числа
, т.е. числа 
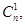
 …,
…,  используются в формуле бинома Ньютона. Их достаточно часто называют биномиальными коэффициентами, поскольку они являются коэффициентами в разложении бинома Ньютона.
используются в формуле бинома Ньютона. Их достаточно часто называют биномиальными коэффициентами, поскольку они являются коэффициентами в разложении бинома Ньютона. )
)

 .
.



