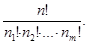Элементы комбинаторики: Перестановки, Размещения, Сочетания

Задача 1Д-Т3. Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькими способами он может выбрать приглашенных?

 

Задача 2Д-Т3. Из группы в 25 человек нужно выделить на дежурство 3 человека. Сколькими различными способами это можно сделать?

 

Задача 3Д-Т3. В урне находятся 10 белых, 15 черных и 20 красных шаров. Из урны наудачу берутся 9 шаров. Найти:

а) сколькими различными способами можно вынуть 9 шаров?

б) сколькими различными способами можно вынуть 9 шаров, среди которых 6 белых и 3 черных?

в) сколькими различными способами можно вынуть 9 шаров, из которых 2 белых, 3 черных и 4 красных шара?

 

Задача 4Д-Т3. Сколько различных вариантов хоккейной команды можно составить из 9 нападающих, 5 защитников и 3 вратарей, если в состав команды должны входить 3 нападающих, 2 защитника и 1 вратарь?

Задача 5Д-Т3. Из коробки, в которой лежат пять пирожных «эклер» и семь — «наполеон», достали пять пирожных. Найти вероятность того, что среди них два «эклера» и три «наполеона».

 

Задача 6Д-Т3. В коробке находятся 50 деталей, из которых 10 бракованных. Из коробки берут наудачу партию в 5 деталей. Найти вероятность того, что в эту партию попали 3 бракованных.

 

Задача 7Д-Т3. Из букв разрезной азбуки составлено слово ТРЕУГОЛЬНИК. Ребенок, не умеющий читать, рассыпал эти буквы и затем выбранные четыре буквы собрал в произвольном порядке. Найти вероятность того, что у него получится слово РУЛЬ.

 

Задача 8Д-Т3. Слово АБРАКАДАБРА разрезается на буквы. Буквы перемешиваются. Одна за другой вытаскиваются 5 букв и прикладываются друг к другу слева направо. Найти вероятности событий:

а) А = {случайно сложится слово РАДАР}.

б) В = {случайно сложится слово БАРКА}.

 

Задача 9Д-Т3. Из букв разрезной азбуки составлено слово СТАТИСТИКА. Какова вероятность того, что, перемешав буквы и укладывая их в ряд по одной (наудачу), получим слова:

а) ТИСКИ?

б) КИСКА?

в) КИТ?

г) СТАТИСТИКА?

 

Задача 10Д-Т3. Пять мужчин и 10 женщин случайным образом по трое рассаживаются за 5 столиков. Какова вероятность того, что за каждым столиком окажется мужчина?

Задача 11Д-Т3. Найти вероятность того, что 30 студентов одной группы родились:

а) в разные дни года?

б) в один день года?

в) 8 марта?

г) в разные месяцы года?

д) в сентябре?

е) в разные дни сентября?

 

Задача 12Д-Т3. Какова вероятность того, что участник лотереи «Спортлото – 6 из 49», купивший один билет, угадает правильно

а) 2 номера?

б) 6 номеров?

 

Задача 13Д-Т3. В электричке 12 вагонов. Сколько существует способов размещения 4 пассажиров, если в одном вагоне должно быть не более одного пассажира?

 

Задача 14Д-Т3. Сколькими способами три награды могут быть распределены между 10 участниками соревнований?

 

Задача 15Д-Т3. Из 4 первокурсников, 5 второкурсников и 6 третьекурсников надо выбрать 3 студента на конференцию. Сколькими способами можно осуществить этот выбор, если среди выбранных должны быть студенты разных курсов?

 

Задача 16Д-Т3. Сколькими способами можно расставить на полке 7 различных книг, чтобы определенные три книги стояли

а) рядом?

б) не рядом?

 

Задача 17Д-Т3. Сколькими способами можно рассадить 5 человек за круглым столом? (Рассматривается только расположение относительно друг друга).

 

Задача 18Д-Т3 (чисто женская задача). В гардеробе у дамы три кофточки, две юбки и двое туфель. Все вещи по стилю и цвету хорошо сочетаются. Сколько различных вариантов наряда можно составить, комбинируя эти вещи?

 

Задача 19Д-Т3. На полке наудачу располагают 10 книг.

1) Сколько существует различных способов расположения 10 книг?

2) Сколько существует способов расположения 10 книг, при которых две заранее помеченные книги окажутся рядом?

3) Сколько существует способов различных расположений 10 книг, при которых заранее помеченные три книги окажутся рядом?

 

Задача 20Д-Т3. На трех карточках написаны цифры 1, 2 и 3 (на каждой карточке по одной цифре). Случайным образом из этого набора выбирают последовательно по одной карточке и кладут в ряд, образуя трехзначное число. Какова вероятность того, что образуется число:

а) 321? б) 231?

 

Задача 21Д-Т3. Четыре одинаковых шара пронумерованы числами 1, 2, 3, 4 и сложены в ящик. Случайным образом из ящика извлекают по одному шару. Какова вероятность того, что шары были извлечены в последовательности:

а) 4, 2, 1, 3?

б) 4, 3, 2, 1?

 

Задача 22Д-Т3. Брошены 3 игральные кости. Какова вероятность того, что:

а) на всех костях выпало по 2 очка?

б) на двух костях выпало по 2 очка, а на третьей – 6 очков?

 

Задача 23Д-Т3. В ящике находятся 2 белых и 2 черных шара. Наугад вынимают 2 шара. Найти вероятность, что вынуты:

а) 2 белых шара?

б) белый и черный шары?

 

Задача 24Д-Т3. Из колоды карт в 36 листов наугад вынимают 2 карты. Какова вероятность того, что это: а) Дама треф и Валет пик?

б) две шестерки?

 

Задача 25Д-Т3. Сколько различных «слов», состоящих из трех букв, можно образовать из букв, составляющих слово «БУРАН»? А если «слова» содержат не менее трех букв?

 

Задача 26Д-Т3. Сколькими способами группу учащихся из 8 человек можно разделить на две подгруппы, состоящие из трех и пяти человек?

 

Тема 4. Элементы комбинаторики. Схема выбора с возвращением: Размещения, Сочетания, Перестановки с повторением – 4 часа: 2 часа лекции, 2 часа семинарское занятие

Схема выбора с возвращением.

Размещения с повторениями

Рассматриваются задачи, в которых выбор элементов из данного множества производится с возвращением. В этом случае выбранный из множества элемент возвращается назад в это множество либо автоматически замещается элементом, аналогичным выбранному.

Если при упорядоченной выборке m элементов из n- элементного множества А выбранные элементы возвращаются обратно и вновь упорядочиваются, то говорят о размещениях с повторениями. В отличие от «традиционных» размещений, размещения с повторениями могут отличаться друг от друга: элементами, порядком элементов, количеством повторений элементов.

Число всех размещений из n элементов по m элементов с повторениями обозначается «А с чертой из n по m» - и вычисляется по формуле:

.

 

Сочетания с повторениями

Пусть в Ω имеется m групп элементов, причем в каждой группе элементов достаточно много. Пусть элементы внутри группы неразличимы, но межгрупповые различия имеются.

Число всех сочетаний из n элементов по m с повторениями обозначается символом С с чертой и вычисляется по формуле:

= .

Расчетная формула приводится к виду:

=

 

Перестановки с повторениями

Пусть в упорядоченном множестве с n элементами имеется m различных элементов. Иногда говорят: «пусть множество разбито на несколько, в данном определении – на m - непустых подмножеств». При этом пусть первый элемент повторяется n₁ раз, второй элемент – n₂ раз, …, m -й элемент – n_m раз, причем

n₁ + n₂ + … + n_m = n.

Перестановки из n элементов данного множества называются перестановками с повторениями из n элементов. Число перестановок с повторениями из n, n₁ + n₂ + … + n_m = n элементов обозначается символом Р_n (n₁, n₂,, n ) и вычисляется по формуле:

Р_n (n ₁, n ₂, …, n_m) =