
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя арифметическая величина. Понятие средней арифметическойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средним арифметическим значением (часто его называют просто «среднее») называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности остается неизменным. Исходя из определения, формула для расчета средней арифметической величины имеет вид:
где Результат можно получить как сумму произведений значений признака в каждой группе хi на число элементов в группе с таким количеством. Получим формулу
где n – число групп. Такую форму средней арифметической называют взвешенной арифметической в отличие от простой средней. В качестве «весов» здесь выступают числа единиц совокупности в разных группах. Свойства средней величины Имеется несколько замечательных свойств средней величины. 1. Сумма отклонений индивидуальных значений от среднего значения признака равна нулю. 1.1. Для взвешенной средней сумма взвешенных отклонений равна нулю. 2. Если каждое индивидуальное значение признака умножить или разделить на одно и то же число, то и средняя величина увеличится или уменьшится во столько же раз. 3. Если к каждому индивидуальному значению признака добавить/вычесть постоянное число, то средняя величина возрастет / уменьшится на это же число. 4. Если веса средней взвешенной умножить или разделить на постоянное число, средняя величина не изменится. 5. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической величины меньше, чем от любого другого числа.
Мода Модой дискретной случайной величины Х – обозначается Mo(X) называется значение случайной величины, имеющее наибольшую вероятность. Отметим, что мода – это число, которое встречается чаще всего, а не частота встречаемости этого значения. Если в вариационном ряду имеются два или несколько равных (и даже несколько различных, но больших чем соседние) значений признака, то вариационный ряд считается бимодальным («верблюдоподобным») либо мультимодальным. Это говорит о неоднородности совокупности значений, возможно, представляющей собой «агрегат» нескольких совокупностей с разными модами. Графически мода - это абсцисса самой высокой точки в распределении СВ.
Медиана Если упорядочить данные по величине, начиная с самой маленькой величины, и заканчивая самой большой, то медиана также будет характеристикой усреднения в упорядоченном наборе данных. Определение. Медиана делит упорядоченный ряд значений пополам с равным числом (количеством) значений как выше, так и ниже ее. Или: медиана определяется как величина, относительно которой по крайней мере 50% выборочных значений не меньше и по крайней мере 50% - больше. Медиана (обозначается Исходя из определения, количество значений, расположенных левее и правее медианы на числовой оси, одинаково.
Вариация массовых явлений. «Меры рассеяния» Размах (интервал изменения) Размах – это разность между максимальным и минимальным значением переменой в наборе данных. Размах обозначается R. Размах R является самым простым показателем, который можно получить для выборки:
Понятно, что чем сильнее варьирует признак, тем больше
Математическое ожидание Одной из основных числовых характеристик является математическое ожидание (или взвешенное среднее значение). Определение. Математическое ожидание (оно обозначается МХ или М (Х)) представляет собой среднее ожидаемое значение рассматриваемой случайной величины в больших сериях испытаний с учетом вероятностей принимаемых значений и вычисляемое по формуле: МХ = М (Х) = которая в сокращенной записи выглядит следующим образом:
Или, другими словами: Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности. В серии из большого количества испытаний среднее арифметическое полученных в этой серии значений СВ будет приближаться к ее математическому ожиданию. Этот факт имеет два важных следствия. Следствие 1. Математическое ожидание СВ, распределение которой нам неизвестно, можно оценить средним арифметическим значений в достаточно большой серии ее последовательных испытаний. Более того, чем длиннее серия, тем точнее оценка. Следствие 2. В практически интересных случаях серий испытаний можно оценивать наиболее вероятный результат, исходя из математического ожидания некоторой СВ.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 791; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.9.9 (0.008 с.) |

 = х 1 + х 2 + … + хn =
= х 1 + х 2 + … + хn =  ,
,
 =
= 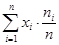 ,
, ) – это так называемое «серединное значение» упорядоченного ряда значений СВ.
) – это так называемое «серединное значение» упорядоченного ряда значений СВ. .
. и наоборот.
и наоборот. ,
,



