
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства средней арифметической. Способы ее исчисления.Содержание книги
Поиск на нашем сайте
Свойства средней арифметической. Способы ее исчисления. Средняя арифметическая обладает рядом математических свойств: 1. Если xi – постоянная величина (xi=C), то ее средняя 2. Сумма отклонений значений признака от его средней арифметической равна нулю: 3. Если все значения признака уменьшить/увеличить на постоянную величину С, то 4. От уменьшения или увеличения частот (fi) каждого значения признака в m раз величина 5. Если все значения признака уменьшить (увеличить) в d раз, то 6. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:
Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина. Если исходные данные не сгруппированы, то используют простую среднюю арифметическую:
Если исходные данные сгруппированы, то используется взвешенная средняя арифметическая:
Если данные сгруппированы и все частоты равны между собой, то можно использовать среднюю арифметическую простую. Если результаты наблюдения представлены в виде интервального ряда распределения, то для расчета средней в качестве xi берутся середины интервалов. Свойства средней арифметической используются для ее расчета способом моментов. (методом отсчета от условного нуля). Он используется в случае вариационных рядов с равными интервалами.
Абсолютные показатели вариации. Их значение в статистическом анализе. Для вариационного ряда важно изучать степень сплоченности всех отдельных значений признака вокруг его среднего значения, степень разбросанности этих значений, степень колеблемости их. Для этого используются показатели вариации, которые делятся на две группы: абсолютные и относительные. К абсолютным показателям относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. 1. Размах вариации R определяется как разность между наибольшим и наименьшим значением признака: 2. Среднее линейное отклонение: средняя арифметическая из абсолютных значений отклонений от их средней: простое среднее линейное отклонение 3. Дисперсия – самый распространенный показатель – величина, полученная из квадратов отклонений вариантов от средней арифметической: простая дисперсия - В ряде случаев для обеспечения более удобного и простого расчета и исключения погрешностей вычислений из-за ошибок округления применяется способ моментов:
4. Среднее квадратическое отклонение Простое среднее квадратическое отклонение - Взвешенное среднее квадратическое отклонение - Использование метода группировок для изучения взаимосвязи между социально-экономическими явлениями. Эмпирическое корреляционное отношение. Для оценки степени связи исследуемого признака с группировочным рассчитывается корреляционное отношение. Изменяется от 0 до 1. 1-функциональная зависимость (значения исследуемого признака определяются полностью группировочным),, 0.3-0.5-умеренная, 0-нет связи,чем ближе к 1, тем теснее связь. Виды ошибок выборки. Предельная ошибка: Средняя ошибка выборки: Собственно-случайный повторный Случайный и механический бесповторный Показатели тесноты связи между количественными признаками (линейный коэффициент корреляции, коэффициент корреляции знаков Фехнера, коэффициент корреляции рангов Спирмена, теоретическое корреляционное отношение). Индексы сезонности. СНС. Принципы построения и классификация счетов в СНС. Основные понятия СНС: резидент, внутренняя экономика, институциональная единица, заведение, сектор экономики, отрасль. Классификация экономических единиц по секторам экономики. Свойства средней арифметической. Способы ее исчисления. Средняя арифметическая обладает рядом математических свойств: 1. Если xi – постоянная величина (xi=C), то ее средняя 2. Сумма отклонений значений признака от его средней арифметической равна нулю: 3. Если все значения признака уменьшить/увеличить на постоянную величину С, то 4. От уменьшения или увеличения частот (fi) каждого значения признака в m раз величина 5. Если все значения признака уменьшить (увеличить) в d раз, то 6. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:
Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина. Если исходные данные не сгруппированы, то используют простую среднюю арифметическую:
Если исходные данные сгруппированы, то используется взвешенная средняя арифметическая:
Если данные сгруппированы и все частоты равны между собой, то можно использовать среднюю арифметическую простую. Если результаты наблюдения представлены в виде интервального ряда распределения, то для расчета средней в качестве xi берутся середины интервалов. Свойства средней арифметической используются для ее расчета способом моментов. (методом отсчета от условного нуля). Он используется в случае вариационных рядов с равными интервалами.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.005 с.) |

 = C
= C
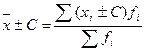



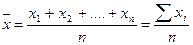

 ;
;  - момент первого порядка (условная средняя)
- момент первого порядка (условная средняя) , где за d берут длину интервала, а за c – середину интервала, находящегося в центре ряда или середину интервала с наибольшей частотой.
, где за d берут длину интервала, а за c – середину интервала, находящегося в центре ряда или середину интервала с наибольшей частотой.
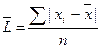 ; взвешенное среднее линейное отклонение
; взвешенное среднее линейное отклонение  ;
; взвешенная дисперсия -
взвешенная дисперсия -  В практических вычислениях удобно рассчитывать дисперсию по следующей формуле:
В практических вычислениях удобно рассчитывать дисперсию по следующей формуле:  , где
, где  - средняя из квадратов значений индивидуальных значений признака
- средняя из квадратов значений индивидуальных значений признака  , а
, а  , где
, где  - моменты соответственно первого и второго порядка, первый исчисляется по формуле:
- моменты соответственно первого и второго порядка, первый исчисляется по формуле:  . Если принять d=1, то формула
. Если принять d=1, то формула 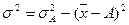 , где
, где  - средний квадрат отклонений индивидуальных значений признака от произвольного числа А:
- средний квадрат отклонений индивидуальных значений признака от произвольного числа А:
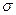 - это корень квадратный из дисперсии. Расчет среднего квадратического отклонения осуществляется по формулам:
- это корень квадратный из дисперсии. Расчет среднего квадратического отклонения осуществляется по формулам:

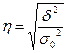
 где t– коэффициент доверия, вычисляемый по таблицам
где t– коэффициент доверия, вычисляемый по таблицам




