
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Схема повторных независимых испытаний с двумя исходамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассматривается случай, когда требуется определить не вероятность осуществления некоторого события Пусть опыт производится многократно, причем выполнены следующие условия: 1) все испытания независимы друг от друга, т.е. вероятность появления события А в каждом из них не зависит от того, произошло или не произошло рассматриваемое событие в других опытах или – опыты являются независимыми, поскольку вероятность исхода каждого опыта не зависит от того, какие исходы имели предшествующие опыты; 2) каждое событие имеет только два исхода: - исход первый - событие А произошло; - исход второй – событие А не произошло, т.е. произошло «не А»; 3) вероятность появления события А в каждом испытании постоянна и равна р, следовательно, вероятность не появления события А – равна q = 1 – p. Такая постановка задачи называется схемой независимых испытаний. Примерами повторных независимых испытаний с двумя исходами могут служить: - многократное подбрасывание сонеты; - стрельба по цели n раз одиночными выстрелами, если нас интересует только попадание или промах; - массовый контроль деталей, при котором требуется только установить, какой является деталь – стандартной или нестандартной.
Некоторые задачи, описываемые схемой независимых повторных испытаний, можно решать, используя формулы для непосредственного подсчета вероятностей или теоремы о вероятности суммы и вероятности произведения. Если же число независимых испытаний n существенно велико, то вычисление вероятности появления события А ровно m раз с помощью теорем о вероятности суммы и вероятности произведения становится трудоемким.
Формула Бернулли Имеется формула, позволяющая непосредственно вычислять вероятность появления события А ровно m раз в серии из n испытаний. При выполнении указанных выше условий вероятность того, что при проведении
где р - вероятность появления события А в каждом испытании, а Иногда употребляют другое обозначение, тождественное введенному нами: P (p, n, m) = Р n(m) = Запишем формулу Бернулли в «развернутом» (факториальном) виде:
Определение. Число k 0 появления события называется наивероятнейшим, если вероятность появления события k раз в серии из n испытаниях превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний. Наивероятнейшее число k 0 определяется из двойного неравенства: (n + 1) p – 1 < k 0 < (n + 1) p, или, что то же самое:
Случай нескольких исходов Если же результатом каждого опыта является не два исхода А и «неА», а несколько взаимно исключающих друг друга исходов: А 1, А 2, …, А s, которые в результате опыта могут появиться с вероятностями р 1, р 2, …, р s соответственно, то вероятность того, что в n опытах событие А 1 появится k 1 раз, событие А 2 – k 2 раз, …, А s – k s раз находится по формуле: Рn (k 1, k 2, …, k s) =
Вероятность появления рассматриваемого события не менее m раз Теорема 1. Вероятность того, что при проведении n независимых испытаний событие А наступит хотя бы один раз, вычисляется по формуле:
Теорема 2. Вероятность того, что при проведении серии из n независимых испытаний событие А наступит не менее k раз, вычисляется по формуле
Отмечу, что вычисление вероятности осуществляется непосредственным суммированием.
Если сумма, стоящая в правой части этого равенства, содержит членов более, чем n/2, то удобнее использовать зависимость между противоположными событиями. Тогда
Задачи, рассмотренные на Лекции и Семинаре 10. Тема 10. Формула Бернулли Лекция 10 Задача 1-Т10. Монета подбрасывается 4 раза. Какова вероятность того, что при этом все четыре раза выпадет Герб?
Задача 2-Т10. Производится три независимых выстрела по цели. Вероятность попадания в цель при каждом выстреле постоянна и равна
Задача 3-Т10. Известно, что при каждом взвешивании равновозможна как положительная, так и отрицательная ошибка. Какова вероятность того, что при пяти взвешиваниях получатся три положительные ошибки?
Задача 4-Т10. Для данного баскетболиста вероятность забросить мяч в корзину при каждом броске составляет 0,4. Что вероятнее ожидать: попадания трех мячей при четырех бросках мяча или попадания четырех мячей при шести бросках мяча, если броски считаются независимыми?
Задача 5-Т10. Испытывается каждый из 15 элементов некоторого устройства. Вероятность выдержать испытания для каждого элемента составляет 0,9. Найти наивероятнейшее число выдержавших испытание элементов и его вероятность.
Задача 6-Т10. Найти наивероятнейшее число выпадений Решки при а) 100 бросаниях монеты; б) 1001 бросании монеты (самостоятельно).
Задача 7-Т10. В цех по ремонту радиоаппаратуры поступают детали с трех заводов в отношении 2:3:5. Мастер для ремонта прибора выбрал наугад 6 деталей. Какова вероятность того, что одна из выбранных деталей изготовлена на первом предприятии, 2 – изготовлены на втором предприятии, 3 – на третьем?
Задача 8-Т10. Найти вероятность того, что в семье, имеющей четырёх детей, будет ровно три мальчика.
Задача 9-Т10. Вероятность солнечной погоды в некоторой местности для каждого дня равна 0,4. Какова вероятность того, что в течение трех дней хотя бы один день будет солнечным?
Задача 10-Т10 (для самостоятельного решения). Стрелок проводит по мишени четыре независимых выстрела. Вероятность попадания в цель при каждом выстреле 0,6. Какова вероятность того, что при этом произойдет не мене трех попаданий?
Семинар 10 Задача 1С-Т10. Вероятность выигрыша лотерейного билета составляет 0,1. Некто покупает 5 лотерейных билетов. Найти вероятности следующих событий: а) А = {ровно два билета выигрывают}, б) В = {б о льшая часть билетов выигрывает}, с) С = {выигрывает хотя бы два билета}.
Задача 2С-Т10. Победу в волейбольном матче одерживает команда, выигравшая 3 партии. Найти вероятность того, что матч между двумя командами, для которых вероятность выигрыша каждой партии равна соответственно 0,8 и 0,2, будет состоять из 5 партий.
Задача 3С-Т10. Система, составленная из четырёх блоков, работает исправно, если за рассматриваемый период выйдет из строя не более двух блоков. Найти вероятность безотказной работы системы блоков, если отказы блоков являются независимыми событиями и вероятность отказа каждого блока равна 1/8.
Задача 4С-Т10. Монету бросают 10 раз. Какова вероятность того, что при этом Герб а) выпадет ровно три раза? б) выпадет меньше двух раз?
Задача 5С-Т10. Студент пишет контрольную работу по теории вероятностей. У него есть предположение о том, как решить задачу, однако свою способность найти правильное решение он оценивает невысоко – примерно 0,4. Вокруг студента в аудитории сидят пять однокурсников. Можно рискнуть опросить их и принять либо отвергнуть решение на основании большинства голосов. Подготовку этих своих однокурсников студент оценивает так же, как и свою. Как лучше поступить студенту: положиться на свои соображения или на большинство голосов однокурсников?
Домашнее задание 10 – Тема 10. Схема Бернулли
Задание 1Д-Т10. Для данного участника игры вероятность наброса кольца на колышек (серсо) равна 0,3. Какова вероятность того, что при шести бросках кольца три кольца окажутся на колышке, если броски считать независимыми?
Задание 2Д-Т10. Вероятность отказа каждого прибора при испытаниях равна 0,4. Что вероятнее ожидать: отказа двух приборов при четырех независимых испытаниях или отказа трех приборов при шести испытаниях?
Задача 3Д-Т10. Партия изделий содержит 5% брака. Какова вероятность того, что среди взятых на испытание четырех изделий одно изделие окажется бракованным?
Задача 4Д-Т10. Производится четыре независимых выстрела по цели. Вероятность попадания в цель при каждом выстреле равна 0,5. Для разрушения цели достаточно хотя бы одного попадания. Какова вероятность того, что цель будет разрушена?
Задача 5Д-Т10. Вероятность хотя бы одного события А в серии из четырех испытаний равна 0,9744. Какова вероятность появления этого события при одном испытании, если в каждом испытании вероятность появления одинакова?
Задача 6Д-Т10. На контрольной работе студентам предложено 10 заданий, на каждое из которых дано два ответа: правильный и неверный. Для получения хорошей оценки студентам достаточно указать не менее 80% правильных ответов. Какова вероятность получения хорошей оценки при простом отгадывании?
Задача 7Д-Т10. Для данного баскетболиста вероятность забросить мяч в корзину при каждом броске равна 0,5. Что вероятнее ожидать: попадания не менее трех мячей в корзину при четырех бросках мяча или попадания не менее четырех мячей при шести бросках, если броски мяча считать независимыми?
Задача 8Д-Т10. Найти вероятность осуществления более двух разговоров по телефону при пяти очередных вызовах, если вероятность состоявшегося разговора равна 2/3.
Задача 9Д-Т10. Из большой связки галстуков, в которой галстуки красного, зеленого и желтого цветов находятся в пропорции 5:3:2, двое мужчин случайным образом выбирают по одному галстуку. Какова вероятность того, что они выберут галстуки одного цвета?
Задача 10Д-Т10. Имеются две урны. В первой находится 1 белый шар, 3 черных и 4 красных, во второй – 3 белых, 2 черных и 3 красных. Из каждой урны извлекают по шару. Найти вероятность того, что цвета выбранных шаров совпадут.
Задача 11Д-Т10. Игральный кубик бросают 5 раз. Найдите вероятность того, что число очков, кратное трем, появится ровно два раза.
Задача 12Д-Т10. Игральный кубик подбрасывают 10 раз. Найти вероятность того, что шестерка выпадет: а) два раза; б) не более восьми раз; в) хотя бы один раз.
Задача 13Д-Т10. Каждый из четырех приятелей выучил ровно 5 вопросов из 20 заданных к зачету. На зачете они отвечали в разных аудиториях и получали вопросы независимо друг от друга. Найти вероятность того, что: а) каждому достался тот вопрос, который он выучил; б) никому не достался вопрос, который он выучил; в) только одному из приятелей достался тот вопрос, который он не выучил; г) хотя бы одному из приятелей достался тот вопрос, который он выучил.
Задача 14Д-Т10. Найдите вероятность «успеха» в каждом из следующих испытаний: а) вытаскивание одной костяшки домино; появление дубля – «неудача»; б) вытаскивание одной костяшки домино; появление костяшки с суммой очков, меньшей четырех – «неудача»; в) вытаскивание одной карты из колоды в 36 карт; появление «пики» - «неудача»; г) вытаскивание одной карты из колоды карт в 36 листов; появление Туза, Короля или Дамы – «неудача».
Задача 15Д-Т10. Какова вероятность того, что при восьми бросаниях монеты: а) Орел выпадет ровно 5 раз? б) Орлов и Решек будет поровну? в) Решка выпадет ровно 5 раз? г) Решка выпадет чаще Орла?
Задача 16Д-Т10. Шахматисты А и В играют несколько партий. Шансы на победу каждого из них в отдельной партии считаются равными. Какой результат А: В оценивается как более вероятный: а) 2: 2 или 3: 1 в четырех партиях? б) 2: 2 в четырех партиях или 3: 3 в шести партиях? в) 3: 1 в четырех партиях или 4: 2 в шести партиях? г) 2: 3 в пяти партиях или 3: 3 в шести партиях?
Задача 17Д-Т10. В соответствии с техническими нормативами вероятность выпуска стандартной детали без дефектов оценивается в 95%. Найдите наивероятнейшее число бракованных деталей среди 1120 выпущенных.
Задача Д-Т10 (Задача Банаха). Некий курящий носит с собой две коробки спичек. Всякий раз, когда необходима спичка, он выбирает наугад одну из коробок. В какой-то момент одна из коробок оказывается пустой. Какова вероятность того, что в этот момент в другой коробке окажется m спичек (m = 0, 1, 2, … n; n – число спичек, бывших первоначально в каждой из коробок)?
Тема 11. Приближенные вычисления в схеме Бернулли. Формулы Пуассона, Муавра – Лапласа. Алгоритмы вычислений. Гауссиана. – 4 часа: 2 часа лекции, 2 часа семинарское занятие
При больших значениях n, порядка десятков и сотен, вместо формулы Бернулли для приближенного вычисления вероятности m успехов в серии n испытаний
Формула Пуассона Если число испытаний n достаточно велико, а вероятность р достаточно мала, причем их произведение Теорема Пуассона. Если число испытаний неограниченно увеличивается
Асимптотическую формулу Пуассона применяют в тех случаях, когда: а) р = const < 0,1, т.е. сам по себе «успех» является редким событием; б) в) n·p·q < 10. Формула Пуассона находит широкое применение в теории массового обслуживания.
Гауссиана, кривая вероятностей. Функция Гаусса
Для гауссовой функции График функции Гаусса называется кривой вероятностей. Пользуясь таблицами значений функции Гаусса, следует помнить, что: 1) 2) Именно поэтому в большинстве таблиц значения функции Теорема 2. Если число испытаний n достаточно велико, а вероятности р и q не очень близки нулю, то приближенное значение вероятности
где Эта замечательная формула называется локальной формулой Муавра – Лапласа.
Алгоритм использования функции Гаусса Для вычисления 1) проверить справедливость неравенства а) n > 100, б) n·p·q > 20; 2) вычислить хk формуле:
3) по таблице значений гауссовой функции вычислить 4) предыдущий результат разделить на
Вероятность того, что число «успехов» k и n испытаниях Бернулли находится в пределах от k 1 до k 2, обозначают так:
Для вычисления вероятностей
(как правило, это условие выполняется при n > 40), то для отыскания вероятности события Для удобства вычислений вводят некоторую дополнительную функцию Ф(х). Для этой функции составлены таблицы значений, а связана она с Если аргумент х положителен, то Ф(х) равна площади под гауссовой кривой на отрезке от [0; 1]. Аналитически Ф(х) записывается с использованием интеграла, именно поэтому полученная в итоге формула называется интегральной. Запись сложна, но ее следует запомнить хотя бы приблизительно.
Следует учитывать, что 1) функция Ф(х) нечетна, т.е. Ф(- х) = - Ф(х), а график функции симметричен относительно начала координат; 2) Ф(х) 3) наконец, Ф(0) = 0. Ясно также, что эта функция возрастает на всей области ее определения. График функции Ф(х) представлен ниже. Функция Ф(х) называется функцией Лапласа.
Теорема 3. В условиях локальной формулы Муавра – Лапласа приближенное значение вероятности
где
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.48 (0.01 с.) |

 в одном испытании, а вероятность того, что это событие произойдет заданное количество раз в серии из
в одном испытании, а вероятность того, что это событие произойдет заданное количество раз в серии из  опытов.
опытов. будет наблюдаться ровно m раз (неважно, в каких именно опытах), определяется по формуле Бернулли:
будет наблюдаться ровно m раз (неважно, в каких именно опытах), определяется по формуле Бернулли: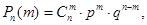
 - вероятность того, что в данном опыте событие А не произошло.
- вероятность того, что в данном опыте событие А не произошло. .
.
 .
.
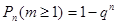 .
.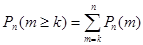 .
.
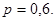 Какова вероятность того, что при этом в мишени будет только одна пробоина?
Какова вероятность того, что при этом в мишени будет только одна пробоина? используются формулы Пуассона и Муавра – Лапласа.
используются формулы Пуассона и Муавра – Лапласа. не мало и не велико, то приближенно вероятность
не мало и не велико, то приближенно вероятность 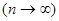 и вероятность р наступления события А в каждом испытании неограниченно уменьшается
и вероятность р наступления события А в каждом испытании неограниченно уменьшается 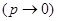 , но так, что их произведение n·p является постоянной величиной (n·p = a = const), то вероятность
, но так, что их произведение n·p является постоянной величиной (n·p = a = const), то вероятность 

 или
или 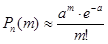 .
. , т.е. количество испытаний n достаточно велико;
, т.е. количество испытаний n достаточно велико;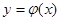 задается формулой
задается формулой .
. - четная функция, т.е.
- четная функция, т.е. 
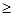 4.
4.
 можно определить по формуле:
можно определить по формуле: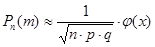 ,
,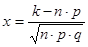 .
. следует:
следует: . Обычно бывает достаточно выполнения условий:
. Обычно бывает достаточно выполнения условий: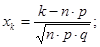



 .
. ,
,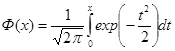 .
. 0,5 при х > 5, поэтому в большинстве таблиц значения функции Ф(х) приведены только для аргумента
0,5 при х > 5, поэтому в большинстве таблиц значения функции Ф(х) приведены только для аргумента  ;
;
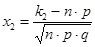 .
.


