
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 11. - Формулы Пуассона и Муавра – ЛапласаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Задача 1-Т11. Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,007. Поступило 1.000 вызовов. Определить вероятность 9 «сбоев».
Задача 2–Т11. Завод «Золотая балка» (Крым) отправил в Москву 1500 бутылок вина «Каберне». Вероятность того, что в пути бутылка может разбиться составляет 0,002. Найти вероятность того, что в пути будет разбито не более 4-х бутылок.
Задача 2–Т11. Завод «Золотая балка» (Крым) отправил в Москву 1500 бутылок вина «Каберне». Вероятность того, что в пути бутылка может разбиться составляет 0,002. Найти вероятность того, что в пути будет разбито не более 4-х бутылок.
Задача 2.1-Т11. Книга в 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице не менее 3 опечаток.
Задача 3-Т11. Вероятность рождения мальчика примем за 0,5. Найти вероятность того, что среди 200 новорожденных будет: а) 110 мальчиков? б) 80 мальчиков (самостоятельно).
Задача 4-Т11. Вероятность того, что при автоматической штамповке изделий отдельное изделие окажется бракованным (т.е. с отклонением от стандарта), постоянна и равна 0,05. а) Какова вероятность того, что в партии из 1000 изделий встретится ровно 40 бракованных? б) Сколько небракованных изделий можно ожидать с вероятностью 0,042?
Задача 5-Т11. Вероятность попадания в цель из скорострельного орудия при отдельном выстреле равна 0,75. Найти вероятность того, что при 300 выстрелах число попаданий будет не менее 210, но не более 230 раз.
Задача 6–Т11 (самостоятельно). Политика П. поддерживает в среднем 40% населения. Какова вероятность того, что из 1500 случайно опрошенных людей политика П. поддерживают от 570 до 630 человек.
Задача 7-Т11. Известно, что 90% жителей некоторой страны ни разу не ели авокадо. Случайным образом выделили n жителей и выяснили число k тех из них, которые не ели авокадо. Насколько большим должно быть n, чтобы с вероятностью более 60% можно было утверждать, что частота
Задача 8-Т11 (дополнительно). Сколько раз нужно подбросить симметричную монету, чтобы с вероятностью 0,90 частота
Задача 9–Т11. Вероятность попадания в мишень при одном выстреле равна 0,6. Найти вероятность того, что при n = 1200 независимых выстрелах отклонение «частости» от вероятности по модулю не превышает
Домашнее задание 11. -Тема 11. Формулы Пуассона и Муавра – Лапласа. Кривая вероятностей (Гауссиана). Закон больших чисел
Задача 1Д-Т11. Найдите значения n, p, q, k и выпишите (без вычислений) формулы для а) вероятность появления ровно 7 Орлов при десяти бросаниях монеты; б) вероятность появления ровно 3 Решек при 10 бросаниях монеты; в) вероятность появления ровно 57 нечетных цифр при 100 независимых выборах одной цифры от 0 до 9; г) вероятность появления ровно 75 цифр, кратных трем, при 100 независимых выборах одной цифры от 0 до 9.
Задача 2Д-Т11. Найдите значения n, p, q, k и выпишите (без вычислений) формулы для а) каждый из 50 человек независимо называет один из дней недели. «Неудачным» днем считается понедельник. Какова вероятность того, что «удач» будет ровно половина? б) каждый из 100 человек независимо называет один из дней недели. «Удачными» днями считаются суббота и воскресенье. Какова вероятность того, что «неудач» будет 33? в) бросание кубика «удачно», если выпадет 5 или 6 очков. Какова вероятность того, что ровно 175 бросаний из 293 будут «удачными»? г) одновременно бросаются три различные монеты. «Неудача» - Решек больше, чем Орлов. Какова вероятность того, что будет ровно три «удачи» в тысяче бросаний?
Задача 3Д-Т11. По таблице значений функции а) б) в) г)
Задача 4Д-Т11. Используя таблицы значений функции а) б) в) г)
Задача 5Д-Т11. Найдите х > 0, для которого значение а) 0,33; б) 0,333; в) 0,1; г) 0,01.
Задача 6Д-Т11. По таблице значений функции Ф найдите: а) Ф(1), Ф(2), Ф(3); б) Ф(0,5), Ф(1,5), Ф(2,5); в) Ф(0,1), Ф(1,1), Ф(2,1); г) Ф(0,9), Ф(0,99), Ф(1,99).
Задача 7Д-Т11. Используя таблицу значений функции Ф, найдите приближенное значение х, если известно, что: а) Ф(х) = 0,3461; б) Ф(х) = 0,4441; в) Ф(х) = 0,004; г) Ф(х) = 0,4904.
Задача 8Д-Т11. Найдите х, для которого значение Ф(х) ближе всего к заданному числу: а) 0,33; б) 0,46; в) 0,1; г) 0,49.
Задача 9Д-Т11. Вероятность рождения мальчика примем равной 0,5. Найдите вероятность того, что среди 900 новорожденных будет:
а) от 400 до 500 мальчиков; б) не менее 440 мальчиков; в) от 430 до 470 девочек; г) не более 460 девочек.
Задача 10Д-Т11. Известно, что из всех поступающих в университет абитуриентов в среднем 60% набрали на экзаменах более 20 баллов. Какова вероятность того, что из 100 случайно выбранных абитуриентов более 20 баллов набрали: а) от 50 до 70 человек? б) не менее 20 человек? в) не более 60 человек? г) более 69 человек?
Задача 11Д-Т11. Известно, что левши составляют в среднем 1% населения. Используя формулы Бернулли, Пуассона и локальную формулу Муавра – Лапласа, найти вероятность того, что среди наугад выбранных 100 человек окажется пятеро левшей.
Задача 12Д-Т11. Предположим, что при наборе книги существует вероятность
Тема 12. Бином Ньютона. Биномиальные коэффициенты. Свойства биномиальных коэффициентов. – 4 часа: 2 часа лекции, 2 часа семинарское занятие Свойства Сочетаний (биномиальных коэффициентов) Сочетания - (a + b)2 = a 2 + 2ab + b 2, (a + b)3 = a 3 + 3a 2 b + 3ab 2 + b 3. Определение. Формула для произвольной степени суммы двух слагаемых выглядит так:
Эту формулу обычно называют формулой бинома Ньютона. Слово «бином» означает «двучлен», а коэффициенты в разложении называются, как мы уже знаем, биномиальными коэффициентами. Треугольник Паскаля Для чисел
Получается бесконечная числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается как сумма двух предшествующих чисел.
Биномиальные коэффициенты обладают многими замечательными свойствами. 1). Все они целые положительные числа. 2). Крайние коэффициенты равны единице. 3). Коэффициенты возрастают от краев к середине. 4). Сумма всех коэффициентов равна 2 n. Это следует из формулы бинома, если в ней положить, что a = b = 1. 5). Сумма биномиальных коэффициентов на четных местах равна сумме коэффициентов на нечетных местах.
6). Если a заменить на -a, то знаки перед биномиальными коэффициентами будут чередоваться. 7). В разложении бинома содержится на один член больше, чем его степень. 8). Разложение есть однородный многочлен, то есть все члены имеют одну и ту же степень относительно a и b; 9). Правило симметрии: для всех m = 0, 1, …, n (записывается:
Правило симметрии удобно использовать в расчетах количества сочетаний 10). Из свойств (7) и (9) следует, что если показатель бинома четный, то в разложении средний член имеет наибольший коэффициент, а если показатель бинома нечетный, то в разложении имеется два средних члена с одинаковым наибольшим коэффициентом. Особенно важное значение имеет следующее свойство. 11). Правило Паскаля или рекуррентное свойство числа сочетаний:
Основная закономерность образования строк состоит в следующем: каждое число в треугольнике Паскаля равно сумме двух чисел, стоящих над ним в предыдущей строке (5 = 1 + 4; 10 = 4 + 6; 6 = 3 = 3 и т.д.). Или то же в строгой формулировке: сумма двух соседних коэффициентов в разложении (а + b) n равна определённому коэффициенту в разложении (а + b) n +1.
Домашнее задание 12 – Тема 12. Бином Ньютона
Задача 1Д-Т12. Раскройте скобки в выражении: а) б) в) г)
Задача 2Д-Т12. Найдите коэффициент при первой степени переменной х у многочлена
Задача 3Д-Т12. Заполнить столбцы треугольника Паскаля до одиннадцатого включительно. В столбцах с номерами 2, 5, 8 и 11 подсчитать суммы, соответствующие средним группам вершин, составляющим третью часть от их общего количества в данном столбце: а) б) в) г) Подсчитать соответствующие вероятности.
Задача 4Д-Т12. По формуле бинома Ньютона раскройте скобки и упростите выражения: а) (х – 2)2; б) (х 2 + Задача 5Д-Т12. Докажите тождество:
Задача 6Д-Т12. Докажите тождество:
Задача 7Д-Т12. Дан бином (2 а 3 + b) n. Найдите n, если сумма всех биномиальных коэффициентов равна 256.
Задача 8Д-Т12. Дан бином (3 а – b) n. Найдите n, если сумма всех биномиальных коэффициентов равна 128.
Задача 9Д-Т12. Найдите член, не содержащий х, в разложении бинома: (3 х +
Задача 10Д-Т12. Найдите член, не содержащий х, в разложении бинома: (х +
Задача 11Д-Т12. Раскройте скобки и упростите выражения: а) (х - б) (3 х +
Задача 12Д-Т12. По формуле бинома Ньютона раскройте скобки и упростите выражения:
а) (х + 2)5; б) (х –
Задача 13Д-Т12. Раскройте скобки и упростите выражения: а) (х - б)
Тема 13. Случайные величины (СВ). Понятие дискретной случайной величины. Закон распределения дискретной СВ. Сумма, произведение случайных величин. Независимые случайные величины. Графическое представление данных: полигон, гистограмма, диаграмма. – 4 часа: 2 часа лекции, 2 часа семинарское занятие
Случайная величина (СВ) – это величина, принимающая в результате испытаний то или иное числовое значение, но заранее не известно, какое именно. Случайные величины обозначаются, как правило, большими латинскими буквами Х, Y и т.д. С каждой случайной величиной связано некоторое множество чисел – значений, которые она может принимать. Принимаемые СВ значения обозначаются соответствующими малыми буквами: х 1, х 2, …, у 1, у 2, … Например, для СВ Х, Y это будут х, у. В результате испытаний (например, проведенных по расписанию занятий) эти значения могут встречаться с различной частотой или вероятностью. Определение. Правило, устанавливающее соответствие (связь) между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины. Если возможный диапазон значений такой величины представляет собой конечное или счетное множество, она называется дискретной случайной величиной, а если эти значения заполняют целиком некоторый интервал — непрерывной случайной величиной. Для полного описания СВ недостаточно лишь знания ее возможных значений. Необходимо еще знать вероятности этих значений. Любое правило (таблица, функция, график), позволяющие находить вероятности отдельных значений СВ или множества значений этой СВ, называется законом распределения СВ (или просто – распределением). В этом случае говорят, что «СВ подчиняется данному закону распределения».
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 747; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.127.152 (0.012 с.) |

 отличается от 0,9 не более чем на 0,01?
отличается от 0,9 не более чем на 0,01? выпадения Герба отличалась от
выпадения Герба отличалась от  (вероятности выпадения Герба) не более, чем на 0,01?
(вероятности выпадения Герба) не более, чем на 0,01? = 0,05.
= 0,05.
 найдите:
найдите: (1),
(1),  того, что любая буква может быть набрана неправильно. После набора гранки прочитывает корректор, который обнаруживает каждую опечатку с вероятностью
того, что любая буква может быть набрана неправильно. После набора гранки прочитывает корректор, который обнаруживает каждую опечатку с вероятностью  . После корректора – автор, обнаруживающий каждую из оставшихся опечаток с вероятностью
. После корректора – автор, обнаруживающий каждую из оставшихся опечаток с вероятностью  . Найти вероятность того, что в книге со ста тысячами печатных знаков останется после этого не более 10 незамеченных опечаток.
. Найти вероятность того, что в книге со ста тысячами печатных знаков останется после этого не более 10 незамеченных опечаток. при
при  , т.е. числа
, т.е. числа 
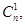
 …,
…,  используются в формуле бинома Ньютона. Их достаточно часто называют биномиальными коэффициентами, поскольку они являются коэффициентами в разложении бинома Ньютона. В школе каждый заучивал формулы квадрата, куба и других степеней суммы двух чисел:
используются в формуле бинома Ньютона. Их достаточно часто называют биномиальными коэффициентами, поскольку они являются коэффициентами в разложении бинома Ньютона. В школе каждый заучивал формулы квадрата, куба и других степеней суммы двух чисел:















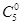










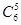
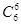
 )
)


 ;
; ;
; ;
; .
. :
:  .
. ;
; ;
; .
. )5.
)5. при k, n
при k, n  N, 1 < k < n.
N, 1 < k < n. при k, n
при k, n  )6
)6 )5;
)5; )6.
)6. )4.
)4. )6;
)6;



