
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства операций над событиямиСодержание книги
Поиск на нашем сайте
1. Переместительный закон А + В = В + А, А·В = В·А. 2. Распределительный закон (А + В) ·С = А·С + В·С, А·В + С = (А + С) · (В + С). 3. Сочетательный закон (А + В) + С = А + (В + С), (А·В) ·С = А· (В·С). 4. Закон «тождественности» А + А = А, А·А = А. 5. Закон «полноты» А + А· 6. Закон «дополнения» А + Ᾱ = А·Ᾱ = Ø. 7. Законы «отрицания» «не Ø» = Ω,
8. Закон «разности» А – В = А· 9. Законы де Моргана
Задачи, рассмотренные на лекции и семинаре. Тема 1. События. Основные операции над событиями Лекция 1 Задача 1-Т1. Из таблицы случайных чисел наудачу взято одно число. Введем события: А = {выбранное число делится на 5}, В = {выбранное число оканчивается нулем}. Выяснить смысл событий а) б)
Задача 2-Т1. Какие из следующих пар событий являются несовместными? совместными? а) А1 = {выход из строя телевизора, работающего в гостиной} и А2 = {на кухне}? б) А3 = {попадание при одном выстреле}, А4 = {промах}; в) А5 = {выпадение герба при подбрасывании монеты}, А6 = {выпадение решки}; г) А7 = {хотя бы одно попадание при двух выстрелах}, А8 = {два попадания}.
Задача 3-Т1 для самостоятельного решения. Из четырех карточек с номерами 1, 2, 3, 4 последовательно наудачу берут две. Составить пространство элементарных событий для этого опыта, если его элементами служат: а) двузначные числа, образованные этими карточками? б) суммы номеров, изображенных на извлеченных карточка?
Задача 4-Т1. Доказать формулу А + В = А +
Задача 5-Т1. В лаборатории работают несколько человек, причем каждый из работников знает хотя бы один иностранный язык. Так, - английский знают 6 человек, - немецкий – 6 человек, - французский – 7 человек, - английский и немецкий – 4 человека, - немецкий и французский – 3 человека, - английский и французский – 2 человека, - все три языка знает один человек. Сколько человек работает в лаборатории? Сколько сотрудников знают только английский язык? Семинар 1 Задача 1С-Т1. Два шахматиста играют одну партию. Вводятся события: А = {выигрывает первый игрок}, B = {выигрывает второй игрок}. Описать события: а) б) в)
Задача 2С-Т1. Упростить выражение (А + В) ·(А +
Задача 3С-Т1. Упростить выражения: а) А·(В – А·В); б) А· в) А + Ᾱ·В +
Задача 4С-Т1. Доказать справедливость законов де Моргана: а) б)
Задача 5С-Т1. Упростить выражения, если известно, что А а) А·В; б) А + В; с) А + В + С.
Задача 6С-Т1. Установите, какие из соотношений правильны: а) Ᾱ + б) в) (А + В) – С = А + (В – С).
Задача 7С-Т1. Совместны ли события А и
Задача 8С-Т1. Справедливы ли, а если «Да», то в каком случае равенства: а) А·В = Ᾱ? б) А + В = Ᾱ?
Задача 9С-Т1. Назвать противоположные события для следующих событий: а) А = {выигрыш первого игрока в шахматной партии}; б) В = {произошло хотя бы одно попадание при десяти выстрелах}; в) С = {произошло три попадания при трех выстрелах}; г) D = {произошло не более двух попаданий при пяти выстрелах}; д) Е = {в семейной паре муж старше жены}.
Задача 10С-Т1. Известно, что события А1 и А2 произошли, а событие А3 не произошло. Произошли ли события: а) б) А1 + А2 ·А3? в) А1 ·А2 ·А3?
Задача 11С-Т1. Каков смысл равенств: а) А·В·С = А? б) А + В + С = А?
Задача 12С-Т1. При каком условии справедливо равенство (А + В) – В = А – В?.
Задача 13С-Т1. Студент пришел на зачет, зная 15 вопросов из 20. Если студент не может ответить на вопрос, ему предоставляется еще одна (не более!) попытка. Каково пространство исходов? Запишите событие А = {студент сдал зачет} через возможные исходы испытания. Какова вероятность сдать зачет?
Домашнее задание 1 – Тема 1. Задача 0Д-Т1. Перечислить все элементарные равновозможные события, которые могут произойти в результате: а) подбрасывания монеты; б) подбрасывания игрального кубика; в) подбрасывания тетраэдра с гранями, занумерованными числами 1, 2, 3, 4; г) раскручивания рулетки, поверхность которой разделена на 5 секторов, обозначенных буквами А, В, С, D, Е.
Задача 1Д-Т1. Одновременно подбрасываются 4 монеты. Вводятся события: - А = {гербов выпало больше, чем цифр}, - В = {выпали все гербы}, - С = {выпали все цифры}. Объяснить смысл событий: а) б) в) г) д) е) Задача 2Д-Т1. Двухмоторный самолет терпит аварию, если одновременно отказывают оба двигателя или выходит из строя система управления. Вводятся события: - А - В = {выходит из строя система управления}, - С = {самолет терпит аварию}. Описать события Задача 3Д-Т1. Доказать формулы: 1) В = А·В + Ᾱ·В. 2) (А+С)·(В+С) = А·В+С.
Задача 4Д-Т1. Пусть А, В и С – три произвольных события. Выразить их через следующие события: а) произошли все три события; б) произошло только С; в) произошло хотя бы одно из событий; г) ни одного события не произошло; д) произошли события А и В, но С не произошло; е) произошло одно из этих событий; ж) произошло не более двух событий.
Задача 5Д-Т1. Событие А влечет за собой В. Что представляют собой события: а) А + В? б) А·В? в) А – В? г)
Задача 6Д-Т1. Пусть событие А = {экзамен сдан}, а событие В = {экзамен сдан на «отлично»}. В чем состоят события: а) А – В? б) «не (А – В)» = в)
Задача 7Д-Т1. Три студента независимо друг от друга решают одну и ту же задачу. Пусть события: А 1 = {первый студент решил задачу}, А 2 = {второй студент решил задачу}, А 3 = {третий студент решил задачу}. Выразить через события 1) А = {все студенты решили задачу}, 2) В = {задачу решил только первый студент}, 3) С = {задачу решил хотя бы один студент}, 4) D = {задачу решил только один студент}.
Задача 8Д-Т1. Из корзины, содержащей красные, желтые и белые розы, выбирается один цветок. Пусть события: - А = {выбрана красная роза}, - В = {выбрана желтая роза}, - С = {выбрана белая роза}. Что означают события: а) б) А + В, в) А·С, г) д) е) А·В + С.
Задача 9Д-Т1. Указать пространство элементарных событий для следующего испытания (опыта) – одновременное подбрасывание двух костей.
Задача 10Д-Т1. В урне находятся 12 пронумерованных шаров. Опыт состоит в извлечении одного шара из урны. Требуется: 1) составить пространство элементарных событий для данного опыта; 2) указать элементарные исходы (события), благоприятствующие событиям: А = {появление шара с нечетным номером}, В = {появление шара с четным номером}, С = {появление шара с номером, большим трех}, D = {появление шара с номером, меньшим 7}; 3) пояснить, что означают события «не В», «не С»; 4) указать, какие из пар А, В, С, D совместны, а какие - нет; 5) привести примеры невозможного и достоверного событий; 7) привести пример другого пространства элементарных событий в данном опыте. Задача 11Д-Т1. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, с сыром и колбасой – 28 человек, с колбасой и ветчиной – 31 человек, с сыром и ветчиной – 26 человек, все три вида бутербродов взяли 25 человек. Несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?
Задача 12Д-Т1. Из событий а) «идет дождь», б) «на небе нет ни облачка», в) «наступила осень» составить все возможные пары и выявить среди них все пары совместных событий и несовместных событий.
Задача 13Д-Т1. Имеется правильная трехгранная пирамида – тетраэдр. Одна из ее граней серая, остальные – белые. Тетраэдр бросают на стол и наблюдают за гранью, которой он соприкасается с поверхностью стола. Являются ли равновозможными события «тетраэдр упал на серую грань» и «тетраэдр упал на белую грань»?
Задача 14Д-Т1. Из полной колоды карт (36 штук) вынимается одна карта. Являются ли равновозможными события: а) «вынута карта черной масти» и «вынута карта красной масти»? б) «вынут Король» и «вынута Дама»? в) «вынута карта бубновой масти» и «вынута карта червонной масти»? г) «вынута карта пиковой масти» и «вынута карта красной масти»? д) «вынута шестерка треф» и «вынута Дама пик»?
Задача 15Д-Т1. Из полной колоды карт вынимается одна карта. Выяснить, являются ли совместными события: а) «вынута карта красной масти» и «вынут Валет»; б) «вынут Король» и «вынут Валет»?
Тема 2. Частость (частота) события. Свойство статистической устойчивости относительной частоты события. Статистическое определение вероятности. Элементы комбинаторики – 4 часа: 2 часа лекции, 2 часа семинарское занятие
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1512; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.28.90 (0.007 с.) |

 =
= 
 = Ø,
= Ø,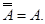
 .
. =
= 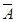 ·
· 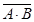 =
=  ;
; .
.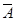 \
\  ;
; ) ·(Ᾱ+В).
) ·(Ᾱ+В). («не (А + В)»).
(«не (А + В)»).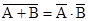 ;
; .
. В:
В: ;
; ?
?



 ={выходит из строя k-двигатель}, k=1, 2;
={выходит из строя k-двигатель}, k=1, 2; ,
,  .
.

 ?
? ?
?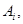
 следующие события:
следующие события: ,
, ,
,


