
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойство статистической устойчивости относительной частоты событияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Пусть в n повторяющихся опытах (испытаниях) некоторое событие А наступило nA раз. Число nA называется частотой события А, а отношение
называется относительной частотой (или частостью) события А в рассматриваемой серии испытаний. Свойства относительной частоты Относительная частота события обладает следующими свойствами. 1. Частота любого события заключена в интервале от нуля до единицы, т.е.
2. Частота невозможного события равна нулю, т.е.
3. Частота достоверного события равна 1, т.е.
4. Частота суммы двух несовместных событий равна сумме частот (частостей) этих событий, т.е. если
Частость обладает свойством, называемым свойством статистической устойчивости: с увеличением числа опытов (т.е. с увеличением n) частость события принимает значения, близкие к вероятности этого события р. Определение. Статистической вероятностью события А называется число, около которого колеблется относительная частота события А Вероятность события А обозначается символом Р (А) или р (А). Появление в качестве символа понятия «вероятность» буквы р определяется ее наличием на первом месте в английском слове probability – вероятность. Согласно данному определению
Свойства статистической вероятности 1. Статистическая вероятность любого события А заключена между нулем и единицей, т.е.
2. Статистическая вероятность невозможного события (А = Ø) равна нулю, т.е.
3. Статистическая вероятность достоверного события (А = Ω) равна единице, т.е.
4. Статистическая вероятность суммы несовместных событий равна сумме вероятностей этих событий, т.е. если А·В = Ø, то
Классическое определение вероятности Пусть проводится опыт с n исходами, которые можно представить в виде группы несовместных равновозможных событий. Случай, который приводит к появлению события А, называется благоприятным или благоприятствующим, т.е. случай w влечет за собой событие А, w Определение. Вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, к общему числу n случаев, т.е.
Свойства «классической» вероятности 1. Аксиома неотрицательности: вероятность любого события А
Р (А) ≥ 0. 2. Аксиома нормированности: вероятность достоверного события (А = Ω) равна единице:
3. Аксиома аддитивности: вероятность суммы несовместных событий (или вероятность появления одного из двух несовместных событий) равна сумме вероятностей этих событий, т.е. если А·В =Ø, то
Вероятность события Для вероятности события, являющегося суммой любых двух событий А и В, справедлива формула:
Если события А и В не могут произойти в результате одного испытания одновременно, т.е. иными словами, если А·В – невозможное событие, то их называют несовместимыми или несовместными, и тогда Р (А·В) = 0 и формула вероятности суммы событий приобретает особенно простой вид:
Если же события А и В могут произойти в результате одного испытания, то их называют совместимыми.
Полезный алгоритм При нахождении вероятностей с использованием классического определения вероятности следует придерживаться следующего алгоритма. 1. Необходимо четко осмыслить, в чем состоит эксперимент. 2. Четко сформулировать, в чем состоит событие А, вероятность которого необходимо найти. 3. Четко сформулировать, что будет в рассматриваемой задаче составлять элементарное событие. Сформулировав и определив элементарное событие, следует проверить три условия, которому должно удовлетворять множество исходов, т.е. Ω. 4. Подсчитать «мощность» Ω, т.е. количество исходов n. 5. Подсчитать число благоприятных исходов, т.е. мощность подмножества А благоприятствующих исходов, составляющую m. 6. Следуя классическому определению вероятности, определить
При решении задач наиболее распространенной ошибкой является нечеткое понимание того, что берется в качестве элементарного события w, а от этого зависит правильность построения множества и правильность вычисления вероятности события. Обычно на практике в качестве элементарного события берут простейший исход, который нельзя «расщепить» на более простые.
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2119; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.32.78 (0.01 с.) |



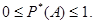
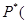 Ø
Ø 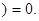

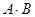 =Ø, то
=Ø, то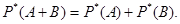
 при достаточно большом числе испытаний (опытов) n.
при достаточно большом числе испытаний (опытов) n.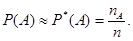
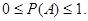
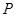 (Ø)=0.
(Ø)=0.
 А.
А.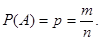
 неотрицательна, т.е.
неотрицательна, т.е. : Р (
: Р ( .
.




