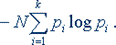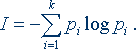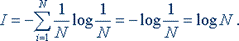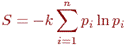Характеристики и свойства информации

Предметы, процессы, явления материального или нематериального свойства, рассматриваемые с точки зрения их информационных свойств, называются информационными объектами.

Информация передаётся в виде сообщений от некоторого источника информации к её приёмнику посредством канала связи между ними. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал. Этот сигнал посылается по каналу связи. В результате в приёмнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.

Примеры:

1. сообщение, содержащее информацию о прогнозе погоды, передаётся приёмнику (телезрителю) от источника — специалиста-метеоролога посредством канала связи — телевизионной передающей аппаратуры и телевизора;

2. живое существо своими органами чувств (глаз, ухо, кожа, язык и т.д.) воспринимает информацию из внешнего мира, перерабатывает её в определенную последовательность нервных импульсов, передает импульсы по нервным волокнам, хранит в памяти в виде состояния нейронных структур мозга, воспроизводит в виде звуковых сигналов, движений и т.п., использует в процессе своей жизнедеятельности.

Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.

Для потребителя информации очень важной характеристикой является ее адекватность. Адекватность информации – это определенный уровень соответствия создаваемого с помощью полученной информации образа реальному объекту, процессу, явлению и т. п.

Адекватность информации может выражаться в трех формах: семантической, синтаксической, прагматической.

Синтаксическая адекватность. Она отображает формально-структурные характеристики информации и не затрагивает ее смыслового содержания. На синтаксическом уровне учитываются тип носителя и способ представления информации, скорость передачи и обработки, размеры кодов представления информации, надежность и точность преобразования этих кодов и т.п.

Семантическая (смысловая) адекватность. Эта форма определяет степень соответствия образа объекта и самого объекта. Семантический аспект предполагает учет смыслового содержания информации. На этом уровне анализируются те сведения, которые отражает информация, рассматриваются смысловые связи

Прагматическая (потребительская) адекватность. Она отражает отношение информации и ее потребителя, соответствие информации цели управления, которая на ее основе реализуется. Проявляются прагматические свойства информации только при наличии единства информации (объекта), пользователя и цели управления. Эта форма адекватности непосредственно связана с практическим использованием информации, с соответствием ее целевой функции деятельности системы.

Свойства информации (с точки зрения бытового подхода к определению информации):

· релевантность(ценность) — способность информации соответствовать нуждам (запросам) потребителя;

· полнота — свойство информации исчерпывающе (для данного потребителя) характеризовать отображаемый объект или процесс; информация полна, если её достаточно для понимания и принятия решений; как неполная, так и избыточная информация сдерживает принятие решений или может повлечь ошибки;

· своевременность(актуальность) — способность информации соответствовать нуждам потребителя в нужный момент времени; только своевременно полученная информация может принести ожидаемую пользу; одинаково нежелательны как преждевременная подача информации (когда она ещё не может быть усвоена), так и её задержка;

· достоверность(адекватность) — свойство информации не иметь скрытых ошибок; достоверная информация со временем может стать недостоверной, если устареет и перестанет отражать истинное положение дел; информация достоверна, если она отражает истинное положение дел; недостоверная информация может привести к неправильному пониманию или принятию неправильных решений;

· доступность — свойство информации, характеризующее возможность её получения данным потребителем; информация должна преподноситься в доступной (по уровню восприятия) форме; поэтому одни и те же вопросы по-разному излагаются в школьных учебниках и научных изданиях.

· защищённость — свойство, характеризующее невозможность несанкционированного использования или изменения информации;

· эргономичность — свойство, характеризующее удобство формы или объёма информации с точки зрения данного потребителя.

Определение информации и меры её измерения в технической концепции. Формулы Р. Хартли и К.Шеннона

В соответствие с выбранной вами специальностью мы будем изучать техническую (прикладную) информатику.

Тогда данные это зарегистрированные сигналы, которые хранятся и передаются на носителях различных видов, существуют объективно.

Методы обработки данных – способы восприятия данных. В основе искусственных методов используются алгоритмы, составленные людьми. Отсюда следует вывод, что методы являются субъективными.

Результатом взаимодействия данных и методов обработки будет информация, а информирование – процесс обработки данных и снятие некоторой неопределенности.

Как измеряется количество информации? Какое количество информации содержится, к примеру, в тексте романа "Война и мир", в фресках Рафаэля или в генетическом коде человека? Ответа на эти вопросы наука не даёт и, по всей вероятности, даст не скоро. Можно ли объективно измерить количество информации? Важнейшим результатом теории информации является следующий вывод:

В определенных, весьма широких условиях можно пренебречь качественными особенностями информации, выразить её количество числом, а также сравнить количество информации, содержащейся в различных группах данных.

То, что мы не знаем, для нас неопределённо, это невозможно количественно оценить. Если некоторое сообщение, полученное человеком, содержит для него информацию, то оно приводит к уменьшению неопределённости наших знаний, т.е. происходит переход от незнания к знанию. Именно такой подход к информации как мере уменьшения неопределённости знаний позволяет её количественно измерить.

Если в сообщении содержалось для вас что-то новое, то оно информативно. Но для другого человека в этом же сообщении нет ничего нового, для него оно неинформативно. Это происходит от того, что до получения сообщения знания каждого из нас различны. Фактор субъективного восприятия сообщения делает невозможным количественную оценку информации в сообщении, т.е. если рассматривать количество полученной информации с точки зрения новизны для получателя, то измерить её невозможно.

В настоящее время получили распространение подходы к определению понятия "количество информации", основанные на том, что информацию, содержащуюся в сообщении, можно нестрого трактовать в смысле её новизны или, иначе, уменьшения неопределённости наших знаний об объекте.

Попытки количественного измерения информации предпринимались неоднократно. Первые отчетливые предложения об общих способах измерения количества информации были сделаны Р. Фишером (1921г.) в процессе решения вопросов математической статистики. Проблемами хранения информации, передачи ее по каналам связи и задачами определения количества информации занимались Р. Хартли (1928г.) и X. Найквист (1924г.). Р. Хартли заложил основы теории информации, определив меру количества информации для некоторых задач. Наиболее убедительно эти вопросы были разработаны и обобщены американским инженером Клодом Шенноном в 1948г. С этого времени началось интенсивное развитие теории информации вообще и углубленное исследование вопроса об измерении ее количества в частности.

Для того чтобы применить математические средства для изучения информации, потребовалось отвлечься от смысла, содержания информации. Этот подход был общим для упомянутых нами исследователей, так как чистая математика оперирует с количественными соотношениями, не вдаваясь в физическую природу тех объектов, за которыми стоят соотношения. Например, если находится сумма двух чисел 5 и 10, то она в равной мере будет справедлива для любых объектов, определяемых этими числами. Поэтому, если смысл выхолощен из сообщений, то отправной точкой для информационной оценки события остается только множество отличных друг от друга событий и соответственно сообщений о них.

Предположим, нас интересует следующая информация о состоянии некоторых объектов: в каком из четырех возможных состояний (твердое, жидкое, газообразное, плазма) находится некоторое вещество? на каком из четырех курсов техникума учится студент?

Во всех этих случаях имеет место неопределенность интересующего нас события, характеризующаяся наличием выбора одной из четырех возможностей. Если в ответах на приведенные вопросы отвлечься от их смысла, то оба ответа будут нести одинаковое количество информации, так как каждый из них выделяет одно из четырех возможных состояний объекта и, следовательно, снимает одну и ту же неопределенность сообщения.

Неопределенность неотъемлема от понятия вероятности. Уменьшение неопределенности всегда связано с выбором (отбором) одного или нескольких элементов (альтернатив) из некоторой их совокупности. Такая взаимная обратимость понятий вероятности и неопределенности послужила основой для использования понятия вероятности при измерении степени неопределенности в теории информации. Если предположить, что любой из четырех ответов на вопросы равновероятен, то его вероятность во всех вопросах равна 1/4. Одинаковая вероятность ответов в этом примере обусловливает и равную неопределенность, снимаемую ответом в каждом из двух вопросов, и, следовательно, каждый ответ несет одинаковую информацию.

Теперь попробуем сравнить следующие два вопроса: на каком из четырех курсов техникума учится студент? Как упадет монета при подбрасывании: вверх «гербом» или «цифрой»? В первом случае возможны четыре равновероятных ответа, во втором – два. Следовательно, вероятность какого-то ответа во втором случае больше, чем в первом (1/2>1/4), в то время как неопределенность, снимаемая ответами, больше в первом случае. Любой из возможных ответов на первый вопрос снимает большую неопределенность, чем любой ответ на второй вопрос. Поэтому ответ на первый вопрос несет больше информации! Следовательно, чем меньше вероятность какого-либо события, тем большую неопределенность снимает сообщение о его появлении и, следовательно, тем большую информацию оно несет.

Предположим, что какое-то событие имеет m равновероятных исходов. Таким событием может быть, например, появление любого символа из алфавита, содержащего m таких символов. Как измерить количество информации, которое может быть передано при помощи такого алфавита? Это можно сделать, определив число N возможных сообщений, которые могут быть переданы при помощи этого алфавита. Если сообщение формируется из одного символа, то N=m, если из двух, то N=m*m=m². Если сообщение содержит n символов (n – длина сообщения), то N=mⁿ. Казалось бы, искомая мера количества информации найдена. Ее можно понимать как меру неопределенности исхода опыта, если под опытом подразумевать случайный выбор какого-либо сообщения из некоторого числа возможных. Однако эта мера не совсем удобна. При наличии алфавита, состоящего из одного символа, т.е. когда m = 1, возможно появление только этого символа. Следовательно, неопределенности в этом случае не существует, и появление этого символа не несет никакой информации. Между тем, значение N при m=1 не обращается в нуль. Для двух независимых источников сообщений (или алфавита) с N₁ и N₂ числом возможных сообщений общее число возможных сообщений N=N1*N2, в то время как логичнее было бы считать, что количество информации, получаемое от двух независимых источников, должно быть не произведением, а суммой составляющих величин.

Выход из положения был найден Р. Хартли, который предложил информацию I, приходящуюся на одно сообщение, определять логарифмом общего числа возможных сообщений N:

I (N)=log N

Если же все множество возможных сообщений состоит из одного (N=m=1), то I(N)=log1=0, что соответствует отсутствию информации в этом случае. При наличии независимых источников информации с N₁ и N₂ числом возможных сообщений

I(N)=logN=log(N₁*N₂)=logN₁+logN₂,

т.е. количество информации, приходящееся на одно сообщение, равно сумме количеств информации, которые были бы получены от двух независимых источников, взятых порознь. Формула, предложенная Хартли, удовлетворяет предъявленным требованиям. Поэтому ее можно использовать для измерения количества информации.

Если возможность появления любого символа алфавита равновероятна (а мы до сих пор предполагали, что это именно так), то эта вероятность р=1/m. Полагая, что N=m,

I=log(N)=log(m)=log(1/p)= –log p, (1)

т.е. количество информации на каждый равновероятный сигнал равно минус логарифму вероятности отдельного сигнала.

Полученная формула позволяет для некоторых случаев определить количество информации. Однако для практических целей необходимо задаться единицей его измерения. Для этого предположим, что информация – это устраненная неопределенность. Тогда в простейшем случае неопределенности выбор будет производиться между двумя взаимоисключающими друг друга равновероятными сообщениями, например между двумя качественными признаками: положительным и отрицательным импульсами, импульсом и паузой и т.п. Количество информации, переданное в этом простейшем случае, наиболее удобно принять за единицу количества информации. Именно такое количество информации может быть получено, если применить формулу (1) и взять логарифм по основанию 2. Тогда

I= –log₂(p)= –log₂(1/2)=log₂2=1

Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита. Название bit образовано из двух начальных букв и последней буквы английского выражения binary unit, что значит двоичная единица. Бит является не только единицей количества информации, но и единицей измерения степени неопределенности. При этом имеется в виду неопределенность, которая содержится в одном опыте, имеющем два равновероятных исхода.

На количество информации, получаемой из сообщения, влияет фактор неожиданности его для получателя, который зависит от вероятности получения того или иного сообщения. Чем меньше эта вероятность, тем сообщение более неожиданно и, следовательно, более информативно. Сообщение, вероятность которого высока и, соответственно, низка степень неожиданности, несет немного информации.

Р. Хартли понимал, что сообщения имеют различную вероятность и, следовательно, неожиданность их появления для получателя неодинакова. Но, определяя количество информации, он пытался полностью исключить фактор «неожиданности». Поэтому формула Хартли позволяет определить количество информации в сообщении только для случая, когда появление символов равновероятно и они статистически независимы. На практике эти условия выполняются редко. При определении количества информации необходимо учитывать не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность их получения.

Наиболее широкое распространение при определении среднего количества информации, которое содержится в сообщениях от источников самой разной природы, получил подход К Шеннона. Рассмотрим следующую ситуацию.

Источник передает элементарные сигналы k различных типов. Проследим за достаточно длинным отрезком сообщения. Пусть в нем имеется N₁ сигналов первого типа, N₂ сигналов второго типа,..., N_k сигналов k-го типа, причем N₁+N₂+...+N_k=N – общее число сигналов в наблюдаемом отрезке, f₁, f₂,..., f_k – частота появления соответствующих сигналов. При возрастании длины отрезка сообщения каждая из частот стремится к фиксированному пределу, т.е.

lim f_i = p_i, (i = 1, 2,..., k),

где р_i можно считать вероятностью сигнала. Предположим, получен сигнал i -го типа с вероятностью р_i, содержащий – log p_i единиц информации. В рассматриваемом отрезке i -й сигнал встретится примерно N*p_i раз (будем считать, что N достаточно велико), и общая информация, доставленная сигналами этого типа, будет равна произведению N*p_i*log р_i. То же относится к сигналам любого другого типа, поэтому полное количество информации, доставленное отрезком из N сигналов, будет примерно равно:

Чтобы определить среднее количество информации, приходящееся на один сигнал, т.е. удельную информативность источника, нужно это число разделить на N. При неограниченном росте приблизительное равенство перейдет в точное. В результате будет получено асимптотическое соотношение – формула Шеннона

В последнее время она стала не менее распространенной, чем знаменитая формула Эйнштейна Е=mc2. Оказалось, что формула, предложенная Хартли, представляет собой частный случай более общей формулы Шеннона. Если в формуле Шеннона принять, что

р₁ = p₂ =... = р_i =... =p_N = 1/N, то

Знак минус в формуле Шеннона не означает, что количество информации в сообщении – отрицательная величина. Объясняется это тем, что вероятность р, согласно определению, меньше единицы, но больше нуля. Так как логарифм числа, меньшего единицы, т.е. log pi – величина отрицательная, то произведение вероятности на логарифм числа будет положительным.

В термодинамике известен так называемый коэффициент Больцмана

k = 1.38 * 10–16 (эрг/град)

и выражение (формула Больцмана) для энтропии или меры хаоса в термодинамической системе:

Сравнивая выражения для I и S, можно заключить, что величину I можно понимать как энтропию из-за нехватки информации в системе (о системе).

Основное функциональное соотношение между энтропией и информацией имеет вид:

I+S(log₂e)/k=const.

Из этой формулы следуют важные выводы:

увеличение меры Шеннона свидетельствует об уменьшении энтропии (увеличении порядка) системы;

уменьшение меры Шеннона свидетельствует об увеличении энтропии (увеличении беспорядка) системы.

Положительная сторона формулы Шеннона – ее отвлеченность от смысла информации. Кроме того, в отличие от формулы Хартли, она учитывает различность состояний, что делает ее пригодной для практических вычислений. Основная отрицательная сторона формулы Шеннона – она не распознает различные состояния системы с одинаковой вероятностью.

5 Понятие термина "информатика"

Понятие информатики многозначно. Существует, по крайней мере, четыре содержательных понимания термина «информатика»: наука, отрасль экономики, сфера человеческой деятельности, технологии.

 

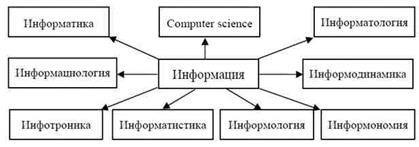
Термин «информатика» появился в начале 60-х гг. (1962 г.) практически одновременно во Франции (Ф. Дрейфус) и у нас в стране (А.А. Харкевич). В 1963 г. в журнале «Известия вузов. Электромеханика», № 11 была опубликована статья Ф.Е. Темникова «Информатика». В ней была сделана попытка определить состав интегральной науки об информации, как совокупность трех составных частей – теории информационных элементов, теории информационных процессов и теории информационных систем. Однако, впоследствии закрепился французский (более узкий) вариант трактовки термина «информатика» (от французского informatique), как науки об ЭВМ и их применении.

Все же первоначально под информатикой у нас понимали науку, связанную, прежде всего, с научной или научно-технической информацией и определяли как научную дисциплину, изучающую структуру и общие свойства научной информации, а также закономерности всех процессов научной коммуникации.

Несмотря на доминирующую роль вычислительной техники (ВТ) в развитии информатики конца 20 века сегодня уже немыслимо простое отождествление информатики с теорией и практикой построения и использования ВТ. Формирование исходных теоретических основ и понятий информатики началось еще до появления первых электронных и даже релейных компьютеров. Своим развитием информатика обязана ряду наук, в том числе математике, логике, теории связи, электронике, теории управления, лингвистике, кибернетике. Так, в математической логике выработаны концепции формального языка, алгоритмов и исчисления в общем смысле. Такие понятия, как булевские функции и машина Тьюринга, оказали прямое влияние на архитектуру компьютеров.

Предлагаются новые наименования – информология, информономия, информациология, информатистика, инфотроника, информатология, информодинамика. Причина их появления заключается в разной трактовке базового понятия - информации. Пока наиболее распространены термины «информатика» и «computer science» (последний – в англоязычных странах), существенно различающиеся по своему содержанию.

Приведем наиболее характерные определения информатики, данные ведущими российскими и зарубежными специалистами в этой области.

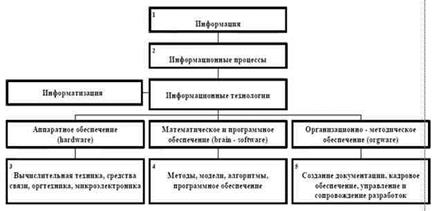
• Информатика – это название фундаментальной естественной науки, изучающей процессы передачи и обработки информации (А.П. Ершов, СССР).

• Информатика – это наука об осуществляемой преимущественно с помощью автоматических средств целесообразной обработке информации, рассматриваемой как представление знаний и сообщений в технических, экономических и социальных областях (Французская академия наук).

• Информатика – это наука, техника и применение машинной обработки, хранения и передачи информации (М.Брой, Германия).

• Информатика – комплекс научно-практических дисциплин, изучающих все аспекты получения, хранения, преобразования, передачи и использования информации. Как наука, она изучает общие закономерности, свойственные информационным процессам.

К компонентам информатики часто относят «привязанную» к ЭВМ триаду: аппаратные средства (hardware), программные средства (software) и методы – модели – алгоритмы (brainware). Считается, что в области создания аппаратных и программных средств информатики Россия отстает от мирового уровня на 10-15 лет. Результаты же фундаментальных исследований, особенно в области brainware, пока не уступают, а нередко превосходят мировой уровень, например, в математическом моделировании, теории программирования, теории передачи информации.

Цифрами на следующем рисунке отмечены основные научные дисциплины, формирующие сегодняшние теоретические основы информатики:

1 – статистическая (шенноновская, классическая) теория (передачи) информации, философские аспекты, качественная теория информации, когнитология, криптография;

2 – теория информационных процессов;

3 – теоретические основы вычислительной техники и вычислительных сетей – теория связи;

4 – теория моделирования, теория языков программирования, теория алгоритмов, инженерия знаний, искусственный интеллект, многоагентные системы, базы данных, распознавание образов, теория роботов;

5 – теория синтеза организационных структур, методы управления разработками и программами.

Перечень этих дисциплин, естественно, будет пополняться и изменяться. Почти все дисциплины, за редким исключением, переживают этап формирования. Наиболее характерным в этом отношении является направление искусственного интеллекта, в рамках которого, по мнению Американской ассоциации искусственного интеллекта, выделяются четыре основных:

• создание интеллектуальных систем моделирования;

• обеспечение интеллектуального доступа к глобальным информационным ресурсам

• создание интеллектуальных тренажеров в различных областях человеческой деятельности;

• создание команд роботов, совместно выполняющих задания в различных, в том числе опасных средах.

В последние годы информатика в России – объект пристального внимания государства. Так, в перечне критических технологий РФ на период до 2010 года, одобренный правительственной комиссией по научно-инновационной политике входили следующие:

1. Высокопроизводительные вычислительные системы;

2. Компьютерное моделирование;

3. Искусственный интеллект;

4. Информационно-телекоммуникационные системы;

5. Элементная база микроэлектроники, наноэлектроники и квантовых компьютеров;

6. Распознавание образов и анализ изображений.